这里写目录标题
- 受伤的皇后
- 全球变暖(最大联通子集,一趟递归记得不要嵌套计数)
- 游园问题
- 金额查错
- 蓝肽子序列(最长公共子序列)
受伤的皇后
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=15;
int a[N][N];
int n,m;
int res=0;
int d[N];
bool ok(int x,int y){
for(int i=1;i<x;i++){
if(d[i]==y)return false;
if(abs(x-i)==abs(y-d[i])){
if(x-i<3)return false;
}
}
return true;
}
void dfs(int u){//当前需要拜访第u行
if(u==n+1){
res++;
return ;
}
for(int i=1;i<=n;i++){
if(ok(u,i)){
d[u]=i;
dfs(u+1);
}
}
}
int main(){
scanf("%d",&n);
dfs(1);
printf("%d",res);
return 0;
}
全球变暖(最大联通子集,一趟递归记得不要嵌套计数)
#include <iostream>
using namespace std;
const int N=1005;
char a[N][N];
bool vis[N][N];
int n,m;
int dx[5]={0,0,1,-1};
int dy[5]={1,-1,0,0};
int res=0;
int ans=0;
bool inside(int x,int y){
return x>=1&&x<=n&&y>=1&&y<=n;
}
bool flag;
void dfs(int u,int v){
if(!flag){
int cnt=0;
for(int i=0;i<4;i++){
int cx=u+dx[i];
int cy=v+dy[i];
if(inside(cx,cy)&&a[cx][cy]=='#')cnt++;
}
if(cnt==4){
ans++;
//只是这样则 一个岛屿中存在x个点不会被淹没就会错判成残余x个岛,
// 其实只有一个
flag=true;
}
}
for(int i=0;i<4;i++){
int cx=u+dx[i];
int cy=v+dy[i];
// if(inside(cx,cy)&&a[cx][cy]=='#')cnt++;
if(inside(cx,cy)&&!vis[cx][cy]&&a[cx][cy]=='#'){
vis[cx][cy]=true;
dfs(cx,cy);
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(a[i][j]=='#'&&!vis[i][j]){
vis[i][j]=true;//本可以不用vis,直接赋值 '.',这里复习一下
res++;//最大联通子集的个数
flag=false;
dfs(i,j);
}
}
}
printf("%d",res-ans);
return 0;
}
游园问题

输入输出样例
输入
WoAiLanQiaoBei
输出
AiLanQiao
这是普通的动态规划,时间复杂度 O ( n 2 ) O(n^2) O(n2),能过70%
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
vector<string> str;
int dp[N];
int main(){
string s,ss;
cin>>s;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]>='A'&&s[i]<='Z'){
if(i)str.push_back(ss);
ss="";
ss+=s[i];
}
else ss+=s[i];
}
str.push_back(ss);
int tail=0;//最长子序列最后一个元素在原数组str中的位置
int len=0;
for(int i=0;i<str.size();i++){
dp[i]=1;
for(int j=0;j<i;j++){
if(str[i]>str[j]){
// if(dp[j]+1>dp[i]){
// dp[i]=dp[j]+1;
// }
dp[i]=max(dp[j]+1,dp[i]);
}
}
if(dp[i]>=len){//不加等号正确率直降10%
// 如果只是求最长子序列的长度,无需加等号,但要求最小字典序的最长子序列
// 为什么此时 长度为len,末尾元素str[i]一定小于 先前遇见的
// 长度为len 末尾元素为str[j]
// 反证法,如果str[j](长度为len)<str[i],那么此时长度一定大于len而不会等于
len=dp[i];
tail=i;
//记录最长子序列的长度 和 最长子序列最后一个元素在原数组中的位置
}
}
// 知道原数组中每一个元素 作为子序列末尾元素对应的子序列长度
// 知道最长子序列的长度和末尾元素在原数组中的位置tail,就可以 从tail开始
// 反向遍历原数组,进而找 对应着长度为len-1子序列的最后一个元
string res="";
for(int i=tail;i>=0;i--){
if(dp[i]==len){
len--;
// res+=str[i];//这样的话还得 reverse(res.begin(),res.end());
res=str[i]+res;
}
}
cout<<res;
return 0;
}
题目意思,给定一串游客字符串,给定的顺序是预约顺序
需要从中选取尽可能多的游客(按游客字典序上升),按预约顺序输出选取的游客
如何保证队列中最后存放的就是最长上升子序列
首先假设队列Q中有一个元素 str【1】
遍历str数组, str【i】> Q.back(),则 str【i】插入队列Q(步骤一)
str【i】< Q.back(),则str【i】可能会小于Q.back()以及
其之前的(按照这种插入Q的方式,Q中元素一定是升序排列的)
那么str【i】应该放在队列中哪个位置->Q中大于str【i】的第一个元素的位置(步骤二)
(反证法可以证明Q中元素是升序的,可以进行二分)

但还没搞懂这贪心怎么证,贪心的道理倒是很容易清楚
队列Q是一路贪心的结果,具有最优子结构(maybe)
首先铁律是上升子序列要尽可能长(步骤一)
相同长度的上升子序列,要尽量保证每一个元素都尽可能小
(在不打乱上升性质的前提下)(动态规划实现的细节就是
相同长度的上升子序列的最大元素应该是尽可能小)(步骤二)
这里最后的队列Q ,可以做到长度为k且最大元素最小的子序列 就是Q(1~k)
(“我们这么理解,同样长度的子序列,是不是末尾的人越矮,
后面可以接着排队的人越多呢?所以这个就是贪心的精髓。”)
如果没理解错的话,拥有了队列Q可以,随时获取 给定长度的最小字典值的上升子序列
而正因为拥有这种性质(长度k-1的子序列字典值越小,更可能获得更长的子序列)
错了,Q队列存放的就是 Q[i]对应的是 长度为i的子序列的最小末尾元素
Q队列根本不是一个完整的最长子序列
好吧,转了一圈还是不知道为什么 遍历str去让更新Q就可以得到Q
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
vector<string> str;
vector<string> Q;
int main(){
string s,ss;
cin>>s;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]>='A'&&s[i]<='Z'){
if(i)str.push_back(ss);
ss="";
ss+=s[i];
}
else ss+=s[i];
}
str.push_back(ss);
Q.push_back(str[0]);
vector<int> len;
len.push_back(1); //Q[0]是长度为1的子序列对应的最后一个元素
for(int i=1;i<str.size();i++){
if(str[i]>Q.back()){
Q.push_back(str[i]);
len.push_back(Q.size());
}
else{
int l=0,r=Q.size()-1;
while(l<r){
int mid=(l+r)/2;
if(Q[mid]>=str[i]){//替换掉Q中第一个大于等于str[i]的元素
// 二分的判断条件要根据题意来决定,不能每次都替换绝对大于她的 可能
// 比如 str[i]是6 ,Q 有一段是 5 6 7 8,不能替换7而应该是6
r=mid;
}
else l=mid+1;
}
Q[l]=str[i];
len.push_back(l+1);
}
}
// 题目要求按预约顺序输出,于是最后按字典序排列的Q用不上
// 相当于需要输出路径,
// 最后得到的有最长子序列的长度sz,
// 可以记录
// str中每个元素作为子序列最后一个元素的子序列长度,其实也就是str中
// 被选中最后放在Q中的元素 在Q中的位置,可能会有多个str中的元素曾
// 试图摆放在Q的同一个位置,但是根据步骤二,一定是str中更后面的元素
// 最终成功留在Q中
// 遍历看str中哪个元素对应的是 长度为sz的子序列的最后一个元素
// 应该从后往前遍历str(更大的长度对应的最后一个元素一定在后面)
//
// 记录str中被选中元素在Q中的位置 或者 记录 Q中选中元素在str中的位置
int sz=Q.size();
int p=str.size()-1;
vector<string> res;
while(sz){
if(len[p]==sz){
sz--;//接下来找Q[sz-1]对应的str中的元素
res.push_back(str[p]);
}
p--;
}
for(int i=Q.size()-1;i>=0;i--){
cout<<res[i];
}
return 0;
}
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
vector<string> str;
vector<string> Q;
int main(){
string s,ss;
cin>>s;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]>='A'&&s[i]<='Z'){
if(i)str.push_back(ss);
ss="";
ss+=s[i];
}
else ss+=s[i];
}
str.push_back(ss);
Q.push_back(str[0]);
vector<int> pos;
pos.push_back(0); //Q[0]是长度为1的子序列对应的最后一个元素
for(int i=1;i<str.size();i++){
if(str[i]>Q.back()){
Q.push_back(str[i]);
pos.push_back(Q.size()-1);
}
else{
int l=0,r=Q.size()-1;
while(l<r){
int mid=(l+r)/2;
if(Q[mid]>=str[i]){//替换掉Q中第一个大于等于str[i]的元素
// 二分的判断条件要根据题意来决定,不能每次都替换绝对大于她的 可能
// 比如 str[i]是6 ,Q 有一段是 5 6 7 8,不能替换7而应该是6
r=mid;
}
else l=mid+1;
}
Q[l]=str[i];
pos.push_back(l);
}
}
// 记录str中被选中元素在Q中的位置 或者 记录 Q中选中元素在str中的位置
int sz=Q.size();
int p=str.size()-1;
vector<string> res;
while(sz){
if(pos[p]+1==sz){//len[p]代表str[p]在Q中的位置 从0存储 子序列最末尾元素的位置+1=子序列长度
sz--;//接下来找Q[sz-1]对应的str中的元素
res.push_back(str[p]);
}
p--;
}
for(int i=Q.size()-1;i>=0;i--){
cout<<res[i];
}
return 0;
}
错误输出路径
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
vector<string> str;
vector<string> Q;
int main(){
string s,ss;
cin>>s;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]>='A'&&s[i]<='Z'){
if(i)str.push_back(ss);
ss="";
ss+=s[i];
}
else ss+=s[i];
}
str.push_back(ss);
Q.push_back(str[0]);
vector<int> pos;
pos.push_back(0);
// pos.push_back(0); //Q[0]是长度为1的子序列对应的最后一个元素
// string pos[N];
for(int i=1;i<str.size();i++){
if(str[i]>Q.back()){
Q.push_back(str[i]);
// pos[Q.size()-1]=i;
pos.push_back(i);
}
else{
int l=0,r=Q.size()-1;
while(l<r){
int mid=(l+r)/2;
if(Q[mid]>=str[i]){//替换掉Q中第一个大于等于str[i]的元素
// 二分的判断条件要根据题意来决定,不能每次都替换绝对大于她的 可能
// 比如 str[i]是6 ,Q 有一段是 5 6 7 8,不能替换7而应该是6
r=mid;
}
else l=mid+1;
}
Q[l]=str[i];
pos[l]=i;
}
}
// 记录str中被选中元素在Q中的位置 或者 记录 Q中选中元素在str中的位置
for(int i=0;i<Q.size();i++){
// cout<<str[pos[i]];
cout<<Q[i];
}
return 0;
}
另一种输出路径,只过了20%,耐心耗尽
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
vector<string> str;
vector<string> Q;
int main(){
string s,ss;
cin>>s;
int cnt=0;
for(int i=0;i<s.size();i++){
if(s[i]>='A'&&s[i]<='Z'){
if(i)str.push_back(ss);
ss="";
ss+=s[i];
}
else ss+=s[i];
}
str.push_back(ss);
Q.push_back(str[0]);
// vector<int> pos;
// pos.push_back(0);
int pos[N];
pos[0]=0;//Q[0]对应的是str[0]中的0位置
int pre[N];
memset(pre,-1,sizeof(pre));
for(int i=1;i<str.size();i++){
if(str[i]>Q.back()){
Q.push_back(str[i]);
pos[Q.size()-1]=i;
pre[i]=pos[Q.size()-2];
}
else{
int l=0,r=Q.size()-1;
while(l<r){
int mid=(l+r)/2;
if(Q[mid]>=str[i]){//替换掉Q中第一个大于等于str[i]的元素
// 二分的判断条件要根据题意来决定,不能每次都替换绝对大于她的 可能
// 比如 str[i]是6 ,Q 有一段是 5 6 7 8,不能替换7而应该是6
r=mid;
}
else l=mid+1;
}
Q[l]=str[i];
pos[l]=i;
pre[i]=pos[l-1];
}
}
int f=pos[Q.size()-1];
stack<int> sta;
while(pre[f] != -1){
sta.push(f);
f = pre[f];
}
sta.push(f);
while(!sta.empty()){
cout<<str[sta.top()];
sta.pop();
}
return 0;
}
正解这种输出路径的方法
#include <bits/stdc++.h>
using namespace std;
char members[999995][12];
char * b[999995];
int p[999995];
int path[999995];
bool cmp(char * x, char * y){
while ( (*x>='a' && *x<='z' || *x>='A' && *x<='Z') && (*y>='a' && *y<='z' || *y>='A' && *y<='Z') ){
if (*x < *y) return true;
if (*x > *y) return false;
x++;
y++;
}
if (*y != 0) return true;
return false;
}
int find(int ll, int rr, char * s){
int mid = (ll+rr)/2;
while (ll<rr){
if ( cmp(b[mid], s) ){
ll=mid+1;
} else {
rr=mid;
}
mid = (ll+rr)/2;
}
return ll;
}
int main(){
memset(path, -1, sizeof(path)-1);
char x;
x = getchar();
int i=-1;
int j=0;
while( x >= 'a' && x <= 'z' || x >= 'A' && x <= 'Z' ){
if ( x >= 'A' && x <= 'Z' ){
i++;
members[i][0] = x;
j=1;
} else {
members[i][j] = x;
j++;
}
x = getchar();
}
b[0] = members[0];
p[0] = 0;
int r=0;
for (int k=1;k<=i;k++){
if ( cmp(b[r], members[k]) ){
r++;
b[r] = members[k];
p[r] = k;
path[k] = p[r-1];
} else {
int pos = find(0, r, members[k]);
if (pos > 0) path[k] = p[pos-1];
b[pos] = members[k];
p[pos] = k;
}
}
int f=p[r];
stack<int> sta;
while(path[f] != -1){
sta.push(f);
f = path[f];
}
sta.push(f);
while(!sta.empty()){
cout<<members[sta.top()];
sta.pop();
}
return 0;
}
解法二用普通数组k可以AC但在dev上崩了,用vector就可以
参考博文
力扣贪心解释
线段树解法
金额查错
一是要去重,二是小的要先去,先递归进 st【u】=true 的分支
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int a[N];
bool f[N];
int m,n;
int sum=0;
void dfs(int u,int s){
if(u==n){
if(s==sum-m){
for(int i=0;i<n;i++)if(f[i])cout<<a[i]<<" ";
cout<<endl;
return;
}
return ;
}
// 出现了两次 3 4 去重,如果数组中没有重复数组选择是不会重复的
// 可以用map存储每次f数组,数组中有两个3,这是根源,但是别忘了a数组是排序好了的
if(u<n&&u > 1) {
if(a[u]==a[u-1]&&f[u-1]==false) {
u++;
}
}//这样可以确保 要么都选 要么只选相同中的第一个
f[u]=true;//金额按照从小到大排列 一定是 先取小的,小的数要先取
dfs(u+1,s+a[u]);
f[u]=false;
dfs(u+1,s);
}
int main(){
cin>>m>>n;
for(int i=0;i<n;i++){
cin>>a[i];
sum+=a[i];
}
sort(a,a+n);
dfs(0,0);
return 0;
}
如果小的数先不取,结果乱套了,选的数超过了m,即使让s>m时推出递归也无济于事
所以还是把小的先取,先递归进 st【u】=true 的分支
蓝肽子序列(最长公共子序列)
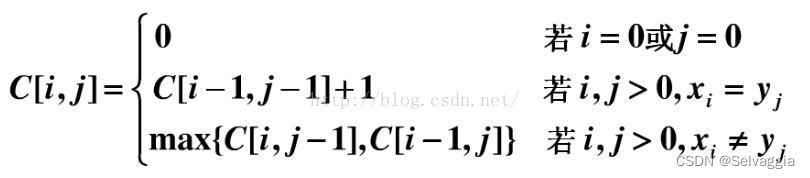
动态规划考虑到 下标-1的位置 不能越界(下届),用vector数组时可以先push 下标为0处任何一个值
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
vector<string> s1,s2;
int dp[N][N];
int main(){//最长公共子序列
string str1,str2;
cin>>str1>>str2;
string ss="*";
s1.push_back(ss);
s2.push_back(ss);
ss="";
for(int i=0;i<str1.size();i++){
if(str1[i]>='A'&&str1[i]<='Z'){
if(i){
s1.push_back(ss);
ss="";
}
ss+=str1[i];
}
else ss+=str1[i];
}
s1.push_back(ss);
ss="";
for(int i=0;i<str2.size();i++){
if(str2[i]>='A'&&str2[i]<='Z'){
if(i){
s2.push_back(ss);
ss="";
}
ss+=str2[i];
}
else ss+=str2[i];
}
s2.push_back(ss);
for(int i=1;i<s1.size();i++){
for(int j=1;j<s2.size();j++){
if(s1[i]==s2[j]){
dp[i][j]=dp[i-1][j-1]+1;
}
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[s1.size()-1][s2.size()-1];
return 0;
}
123(二分)

#include<bits/stdc++.h>
using namespace std;
const int N=1500000;
#define ll long long int
ll a[N];//前缀长度
ll sum[N];//前缀和
ll preSum(ll x){
ll l=1,r=N;//从小往大找,左边界一定要合法,一开始l取成0 1~?区间的求解就会出错,而从右往左这个左边界就,,反正能过
while(l<r){
ll mid=(l+r)>>1;从小往大找
if(a[mid]<x){//找到 a[mid]>=x 且a[mid-1]<x,那么下标x就在第mid行
l=mid+1;
}
else r=mid;
// ll mid = l + r + 1 >> 1;//从大往小找
// if (a[mid] > x) r = mid - 1;//找到 a[mid]<=x 且a[mid+1]>x,那么下标x就在第mid行
// else l = mid;
}
// return sum[l] + a[x - a[l]];
return sum[l-1]+a[x-a[l-1]];
}
int main(){//最长公共子序列
int T;
cin>>T;
// 行数i,(1+i)*i/2<=1e12 i<=sqrt(2)* 1e6 < 150000 序列的长度小于150000
for(int i=1;i<N;i++){
a[i]=a[i-1]+i;
sum[i]=sum[i-1]+a[i];
// 注意前i行的长度 的值 恰好等于 第i行的和
}
ll l,r;
while(T--){
scanf("%lld %lld",&l,&r);
printf("%lld\n",preSum(r)-preSum(l-1));
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int N=1500000;
#define ll long long int
ll a[N];//前缀长度
ll sum[N];//前缀和
ll preSum(ll x){
ll l=1,r=N;//从小往大找,左边界一定要合法,一开始l取成0 1~?区间的求解就会出错
while(l<r){
ll mid = l + r + 1 >> 1;//从大往小找
if (a[mid] > x) r = mid - 1;//找到 a[mid]<=x 且a[mid+1]>x,那么下标x就在第mid行
else l = mid;
}
return sum[l] + a[x - a[l]];
}
int main(){//最长公共子序列
int T;
cin>>T;
// 行数i,(1+i)*i/2<=1e12 i<=sqrt(2)* 1e6 < 150000 序列的长度小于150000
for(int i=1;i<N;i++){
a[i]=a[i-1]+i;
sum[i]=sum[i-1]+a[i];
// 注意前i行的长度 的值 恰好等于 第i行的和
}
ll l,r;
while(T--){
scanf("%lld %lld",&l,&r);
printf("%lld\n",preSum(r)-preSum(l-1));
}
return 0;
}