文章目录

前言
一、历年考题
- 1.1 判断题
- 1.2 单选题
- 1.3 复杂度计算
- 1.4 分治
- 1.5 算法设计（01背包，最短路径）
- 1.6 最大子数组问题
- 1.7 算法设计（最长回文串）
二、核心考点
- 2.1 概述部分考点
- - 2.1.1 循环不变式loop-invariants
  - 2.1.2 RAM模型
- 2.2 分治算法
- - 2.2.1 分治算法求解方法
  - 2.2.2 快速排序，归并排序，堆排序
  - 2.2.3 主定理
- 2.3 线性时间排序算法
- 2.4 动态规划
- - 2.4.1 动态规划求解步骤
  - 2.4.2 动态规划要素
  - 2.4.3 动态规划具体求解问题
- 2.5 贪心算法
- - 2.5.1 贪心算法求解步骤
  - 2.5.2 贪心算法要素
  - 2.5.3 贪心算法具体问题求解
- 2.6 搜索算法和NP问题

前言

主要针对西安电子科技大学《算法分析与设计》的核心考点进行汇总，包含总共7章的核心知识点。
【期末期间总结资料如下】
在这里插入图片描述
针对西电计科院软件工程专业大三下学期的《算法分析与设计》期末考试复习资料。大部分知识点来自于张立勇老师的PPT，放心使用。
考试主要包括：判断题，单选题，简答题（各类算法的计算题）
（如需要算法分析与设计全部笔记资料以及历年考题答案，可以联系邮箱oax_knud@163.com

一、历年考题

1.1 判断题

Answer T/F for the following: (2 * 8 points)
(1) 5n2 - 2n + 1024 ∈ ∈ O(n)
(2) 5n2 - 2n + 1024 ∈ ∈ Ω(n)
(3) 5n2 - 2n + 1024 ∈ ∈ Θ(n2)
(4) The array A 87 85 72 84 79 75 70 55 68 forms a max-heap.
(5) If a sorting algorithm is NOT stable, then the output of the algorithm may be NOT in correctly sorted order.
(6) In Dynamic Programming strategy, optimal substructure means that an optimal solution to the problem contains within it an optimal solution to subproblems.
(7) Greedy strategy can be used to obtain an optimal solution of the 0-1 knapsack problem by choosing the most value/ weight per unit in descending order.
(8) 3-COLOR problem is an NP-Complete problem.

在这里插入图片描述

1.2 单选题

2 ． Single Choice (2*10 points)
(1) The average-case running time of Insertion Sort is ( )
A. Θ(n 2 ) B. Θ(nlgn) C. Θ(n) D. Θ(n 3 )
(2) The worst-case running time of Merge Sort is ( )
A. Θ(n 2 ) B. Θ(nlgn) C. Θ(n) D. Θ(n 3 )
(3) The worst-case running time of Quick Sort is ( )
A. Θ(n 2 ) B. Θ(nlgn) C. Θ(n) D. Θ(n 3 )
(4) Which of the following sorting algorithm is NOT stable ( )
A. Heap Sort B. Merge Sort
C. Insertion Sort D. Counting Sort
(5) Which of the following sorting algorithm is NOT in place ( )
A. Quick Sort B. Bucket Sort
C. Heap Sort D. Insertion Sort
(6) Which designing strategy is used in Quick Sort ( )
A. Divide and conquer B. Dynamic programming
C. Greedy D. Brute Force
(7) Which designing strategy is used in Assembly-Line Scheduling problem ( )
A. Divide and conquer B. Dynamic programming
C. Greedy D. Brute Force
(8) Which designing strategy is used in Activity Selection problem ( )
A. Divide and conquer B. Dynamic programming
C. Greedy D. Brute Force
(9) In the DP recursive equation used for Longest Common Subsequence problem,
c[i,j] represents the ( ) of x[1…i] and y[1…j], it’s the ( ) of the problem.
A. longest common subsequence B. length of longest common subsequence
C. optimal solution D. value of optimal solution

在这里插入图片描述

1.3 复杂度计算

Evaluate the following recursions using the Master Method (3 * 4 points)
(1) T(n) = 5T(n/2) + n 2
(2) T(n) = 4T(n/2) + n 2
(3) T(n) = 3T(n/2) + n 2

在这里插入图片描述

1.4 分治

Divide and Conquer Strategy (12 points)
(1) Describe the 3 steps used in Divide and Conquer strategy to solve a problem.
(2) Given the following array A to be sorted using Quick Sort as following:10 9 8 5 4 11 7 6
using the last element (6) as pivot, give the result of the total array after the first partition.
(3) Mark the two sub-problems remained in question (2), describe the following
steps in Quick Sort for this instance.

在这里插入图片描述

1.5 算法设计（01背包，最短路径）

Design Strategies(16 points)
Answer the following questions briefly.
(1) To calculate the optimal solution for Fractional Knapsack problem and 0-1
Knapsack problem, which problem can solved using Greedy strategy? Which
problem can be solved using Dynamic Programming strategy? Describe the main
idea of the two corresponding algorithms.
(2) When solving the Single-Source Shortest Path problem, there may be negative
edge(s) or not, in which case Greedy strategy (Dijkstra) can be used to get the
optimal solution? Describe the main idea of Dijkstra algorithm. How to calculate
the length of the shortest paths in the other case?

在这里插入图片描述

1.6 最大子数组问题

Maximum Subarray Problem (16 points)
Maximum Subarray Problem means to find the subarray indexed from i to j
which maximize the sum of A i ~A j . You should notice that there may be negative
ones but not all in the input array A[1…n].
(1) Give an algorithm to calculate the maximum subarray in O(n 2 ) time, using Brute-Force or Divide and Conquer strategy as you like.
(2) How to solve the problem in O(n) time using Dynamic Programming strategy?
Give and describe the recursive equation used in the optimal substructure of the DP algorithm.
(3) Given the following input array as following, used the algorithm in step (2) to
calculate the maximum subarray.8 -5 -4 10 -1 7 -3 12 -20 18

答案以后再补充~

1.7 算法设计（最长回文串）

Algorithm Design(8 points) Design an algorithm to find the longest palindrome( 回文 ) subsequence for a given string S. A subsequence is a sequence that can be derived from a string by deleting some chars without changing the order of the remaining ones. A palindrome is a symmetrical string, that is, a string read identically from left to right as well as from right to left. For example, one longest palindrome subsequence of string “DABBEAF” is “ABBA”, whose length is
( NOTICE: You’re NOT allowed to use the algorithm for Longest Common Subsequence problem! )

答案以后再补充~

二、核心考点

2.1 概述部分考点

2.1.1 循环不变式loop-invariants

1、初始化：在循环第一次迭代前为真
2、维护：如果在循环的一次迭代前为真，则在下一次迭代之后保持为真
3、终止：当循环终止时，循环不变量提供一个属性表明算法是否正确。

2.1.2 RAM模型

1、指令一个接一个执行，无并发操作
2、程序中每一条指令均为原子操作，包括算术运算，逻辑运算，数据移动，控制运算【无嵌套指令和中断】
3、每一种指令执行时间固定
4、内存容量足够大

2.2 分治算法

分治算法主要包括了如下部分的内容：
在这里插入图片描述

2.2.1 分治算法求解方法

分：将问题分解为若干较小规模的子问题，子问题相互独立，与原问题形式相同。
治：递归求解每个子问题。
合：将子问题的解合并，得到原问题的解。

2.2.2 快速排序，归并排序，堆排序

需要掌握快速排序，归并排序，堆排序的详细计算过程以及时间复杂度。

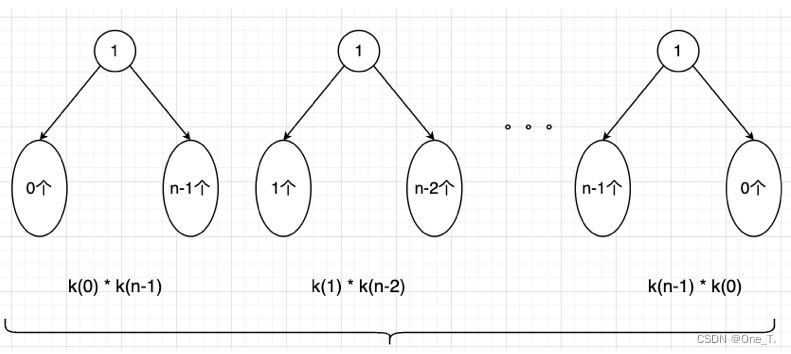
2.2.3 主定理

对于T(n)=aT(n/b)+f(n)
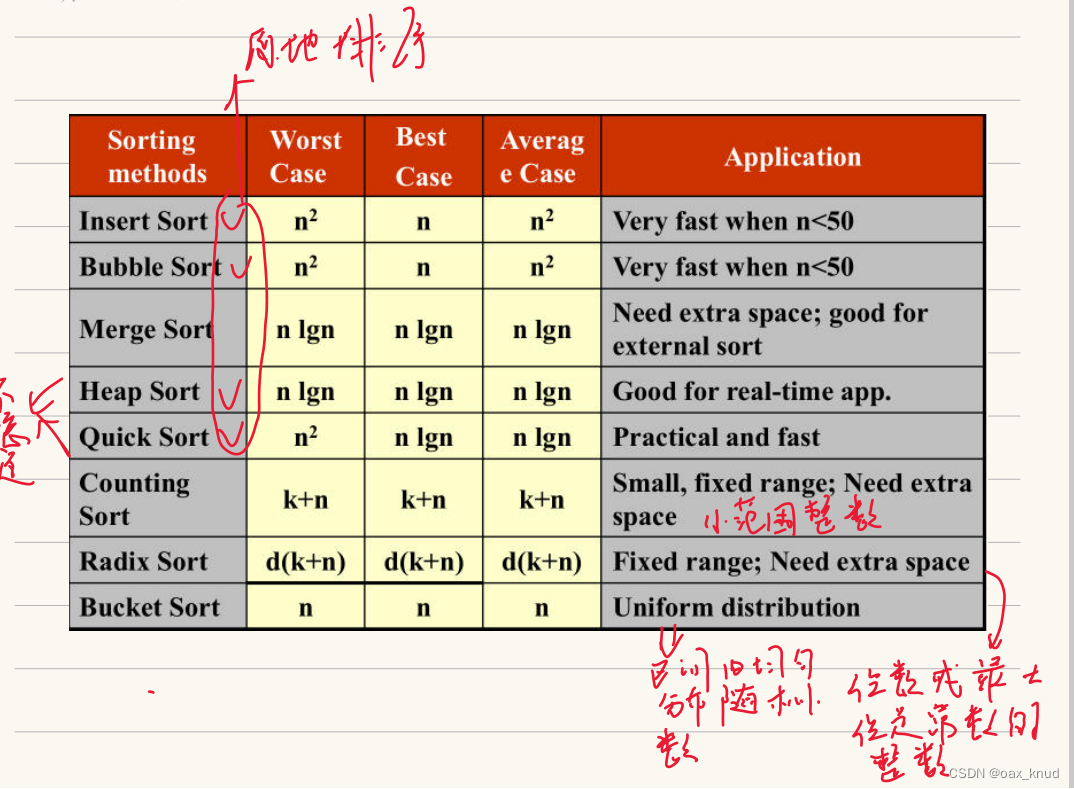
在这里插入图片描述

2.3 线性时间排序算法

线性时间排序算法主要包括如下内容：
在这里插入图片描述
掌握以上排序算法的原理，计算过程，时间复杂度，使用场景，是否稳定。
对比各种算法。

2.4 动态规划

动态规划主要包括了如下部分的内容：
在这里插入图片描述
很多问题可以同时通过分治算法和动态规划两种方法进行解决，在学习过程中最好掌握多种方法，在考场中可以随机选择喜欢的方法进行伪代码书写。

2.4.1 动态规划求解步骤

（1）分析最优解的性质，并刻画其结构特征（最优子结构）。
（2）递归的定义最优解。
（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值
（4）根据计算最优值时得到的信息，构造问题的最优解

2.4.2 动态规划要素

1、最优子结构
（1）、定义：一个问题的最优解包含子问题的最优解
（2）、差异性：一个问题包含了多少个子问题；最优解中使用了哪些子问题
2、重叠子问题overlapping subproblems
（1）、若在代码中直接使用递归会出现重复子问题的情况
在这里插入图片描述
3、重构最优解：通过一个和存储最优解的值相同结构的数据结构记录子问题的最优解，通过子问题的最优解重构问题的最优解。

2.4.3 动态规划具体求解问题

装配线调度问题，矩阵链乘，最长公共子序列，01背包问题，最大子数组问题，最长公共子串，活动选择问题。需要完全掌握以上问题的求解思路以及计算过程，时间复杂度。
以装配线调度问题为例进行分析。
1、问题重述
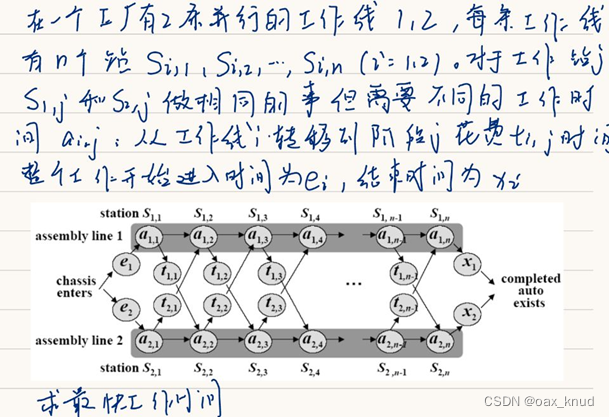
在这里插入图片描述
2、核心思路
（1）、最优子结构：
首先划分子问题，由于站点S[1][j]和S[2][j]分析过程相同，在这里选择S[1][j]进行分析。对于站点S[1][j]来说，若j=1，则其最短工作时间仅考虑e1；若j>1，则其最短工作时间有两种可能：
任务直接从上一个站点S[1][j-1]交付至S[1][j]，所花费的时间为任务到在站点S[1][j-1]为止花费的时间加上站点S[1][j]工作时间。
任务从站点S[2][j-1]经过转移时间t[2][j-1]到达S[1][j]，然后在进行巩固走，所花费的时间为任务到在站点S[2][j-1]为止花费的时间，站点S[1][j]工作时间，任务转移时间t[2][j-1]。
可以认为S[1][j]的最短工作时间是取这两种可能中的最短工作时间。
（2）、递归式：f[i][j]表示i工作先第j个站点工作后所需要的最短工作时间，由最优子结构可以得到如下递归式：
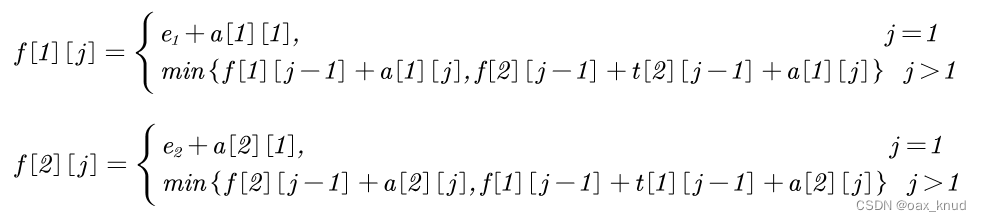
在这里插入图片描述
（3）、最优解：

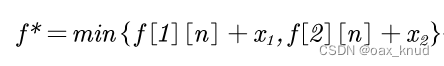
（4）、构造最优解：采取与f相同的数据结构d[i][j]记录在最短工作时间的情况下，站点S[i][j]的上一个工作站来源于第i条工作线。

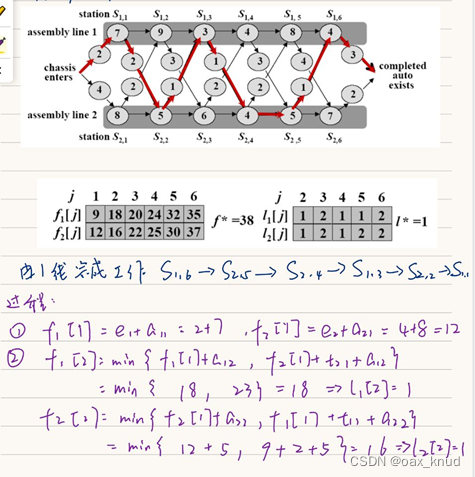
3、伪代码书写在这里插入图片描述

4、具体计算题分析

2.5 贪心算法

贪心算法覆盖的内容包括：
在这里插入图片描述

2.5.1 贪心算法求解步骤

1、建立数学模型来描述问题；
2、把求解的问题分成若干个子问题；
3、对每一子问题求解，得到子问题的局部最优解；
4、把子问题的解局部最优解合成原来解问题的一个解

2.5.2 贪心算法要素

1、贪心选择【贪心算法与动态规划算法的主要区别】
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择来达到。贪心选择是采用从顶向下、以迭代的方法做出相继选择，每做一次贪心选择就将所求问题简化为一个规模更小的子问题。

2、最优子结构
当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。运用贪心策略在每一次转化时都取得了最优解。
贪心算法的每一次操作都对结果产生直接影响，而动态规划则不是。贪心算法对每个子问题的解决方案都做出选择，不能回退；动态规划则会根据以前的选择结果对当前进行选择，有回退功能。动态规划主要运用于二维或三维问题，而贪心一般是一维问题

2.5.3 贪心算法具体问题求解

活动选择问题，分数背包问题，哈夫曼算法，最短路径问题。需要掌握核心原理，伪代码，时间复杂度等相关知识。
这里以活动选择问题进行分析
1、问题重述
在这里插入图片描述

2、核心原理
首先，按照活动的结束时间顺序进行升序排序，然后对于活动i到活动j最多可以选择多少不冲突的活动这个问题，将其划分为两个子问题进行考虑。首先选择活动k作为子问题划分的断点，k满足：
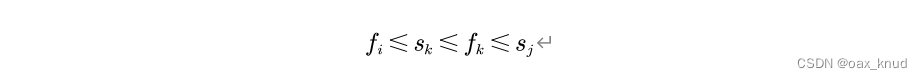
在这里插入图片描述
活动i到活动j之间最多不冲突活动数目等于活动i到k之间最多不冲突活动数目+活动k到j之间最多不冲突活动数目。
根据贪心原理，选择sij中最早结束的活动作为k最问题进行划分，由于k为最早结束的活动，因此在k之前的活动不存在，所以子问题的个数减少为1个。仅需求活动k到j之间最多不冲突活动数目即可·。