一个up的理解
一、二分查找基础例题
力扣![]() https://leetcode.cn/problems/binary-search/
https://leetcode.cn/problems/binary-search/
二、二分查找模板问题
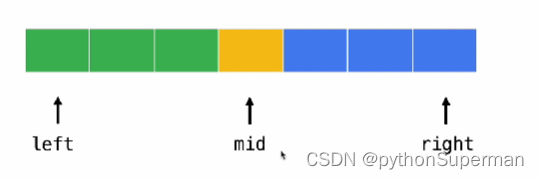
带搜索区间分为3个部分:
1、[mid],直接返回
2、[left,mid-1],设置边界right = mid - 1
3、[mid+1,right],设置边界left = mid + 1
三、二分查找法的另一种思路
- 排除法:考虑中间元素nums[mid]在什么情况下不是目标元素
- 思路:把待搜索区间分为两部分,一部分一定不存在目标元素,另一部分可能存在目标元素,根据中间元素mid被分到左边区间还是右边区间,有以下两种情况。

四、用“排除法”(减治思想)写二分查找问题的一般步骤:
1、把循环终止的条件写成while(left<right);
2、写if和else语句的时候,思考当nums[mid]满足什么性质时,nums[mid]不是目标元素,接着判断mid的左边有没有可能存在目标元素,mid的右边有没有可能存在目标元素。
3、根据“边界收缩的行为”修改取中间数的行为(重难点)
(1)int mid = (left+right)/2;在left和right较大的时候会发生整形溢出。
建议的写法:int mid = left + (right - left)/ 2
(2)“/”是整数除法,默认的取整行为是下取整,那么它会带来一个问题;
int mid = left + (right - left)/ 2;永远取不到有边界right
在面对left = mid 和 right = mid - 1这种边界收缩行为时,就有可能产生死循环。
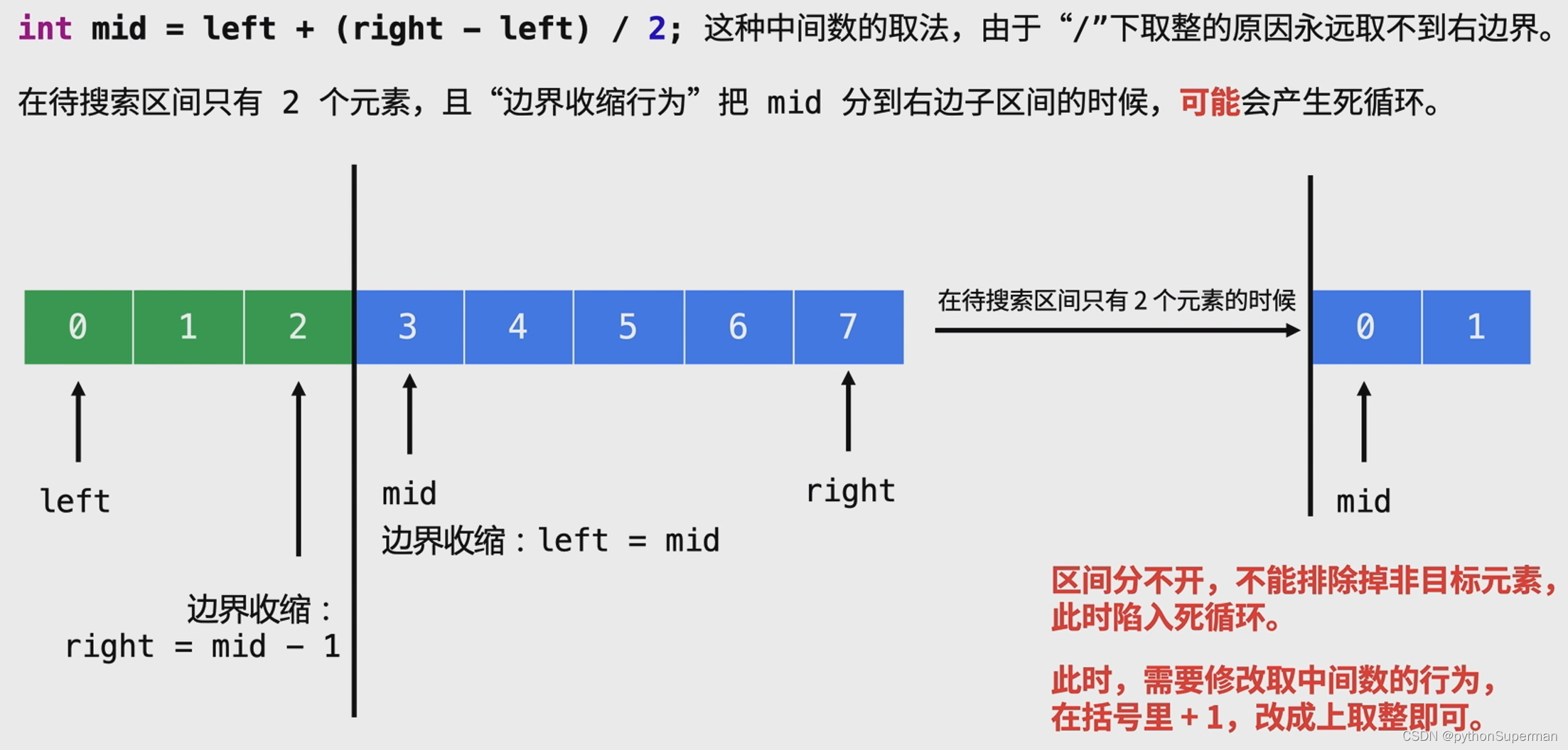
死循环:left一直指向0,right一直指向1
4、退出循环以后,看是否需要对num[left]是否是目标元素再做一次检查。
第二个up的理解
https://leetcode.cn/problems/binary-search/solution/er-fen-cha-zhao-xiang-jie-by-labuladong/
写的很详细,我这里展示三种情况的二分查找算法。
第一个,最基本的二分查找算法:
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回
第二个,寻找左侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界
第三个,寻找右侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right,必须减一对于寻找左右边界的二分搜索,常见的手法是使用左闭右开的「搜索区间」,我们还根据逻辑将「搜索区间」全都统一成了两端都闭,便于记忆,只要修改两处即可变化出三种写法:
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 最后要检查 left 越界的情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 最后要检查 right 越界的情况
if (right < 0 || nums[right] != target)
return -1;
return right;
}
如果以上内容你都能理解,那么恭喜你,二分查找算法的细节不过如此。
通过本文,你学会了:
1、分析二分查找代码时,不要出现 else,全部展开成 else if 方便理解。
2、注意「搜索区间」和 while 的终止条件,如果存在漏掉的元素,记得在最后检查。
3、如需定义左闭右开的「搜索区间」搜索左右边界,只要在 nums[mid] == target 时做修改即可,搜索右侧时需要减一。
4、如果将「搜索区间」全都统一成两端都闭,好记,只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可,推荐拿小本本记下,作为二分搜索模板。
例题:
题目:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
通过次数901,475提交次数1,654,035
第一个,最基本的二分查找算法:
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
left = 0
right = len(nums)-1
while left <= right:
mid = left + (right - left)//2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
return mid
return -1第二个,寻找左侧边界的二分搜索:
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
left = 0
right = len(nums)-1
while left <= right:
mid = left + (right - left)//2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
right = mid - 1
if left >= len(nums) or nums[left] != target:
return -1
return left第三个,寻找右侧边界的二分查找
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
left = 0
right = len(nums)-1
while left <= right:
mid = left + (right - left)//2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
left = mid + 1
if right < 0 or nums[right]!=target:
return -1
return right