- 文章题目: KGE-CL: Contrastive Learning of Knowledge Graph Embeddings
- 时间:2021
摘要
- 学习知识图的嵌入在人工智能中至关重要,可以使各种下游应用受益,如推荐和问答。近年来,人们对知识图嵌入进行了大量的研究。然而,以往的知识图嵌入方法大多采用打分函数对每个三元组分别进行优化,忽略了不同三元组中相关实体和实体-关系对之间的语义相似性。针对这一问题,我们提出了一种简单高效的知识图嵌入对比学习框架,该框架可以缩短不同三元组中相关实体和实体-关系对之间的语义距离,从而提高知识图嵌入的表达能力。我们在三个标准的知识图谱基准上评估我们提出的方法。值得注意的是,我们的方法可以产生一些新的最先进的结果,在WN18RR数据集上实现51.2%的MRR, 46.8%的Hits@1,在YAGO3-10数据集上实现59.1%的MRR, 51.8%的Hits@1。
引言
- 知识图谱(KG)以三元组的形式存储了大量的人类知识。知识图中的三元(h, r, t)包括头部实体h,尾部实体t,以及h与t之间的关系r。知识图嵌入(KGE)旨在将知识图中大量相互关联的实体和关系投射到向量或矩阵中,以保留三元组的语义信息。学习知识图的嵌入可以使各种下游人工智能应用受益,如问答(Huang et al 2019)、机器阅读理解(Yang and Mitchell 2017)、图像分类(Marino, Salakhutdinov, and Gupta 2016)和个性化推荐(Wang et al 2018)。
- 一般来说,大多数KGE方法都会定义一个评分函数 f ( h i , r j , t k ) f(h_i, r_j, t_k) f(hi,rj,tk),知识图嵌入的训练目标是最大化一个真三重 ( h i , r j , t k ) (h_i, r_j, t_k) (hi,rj,tk)的评分和最小化一个假三重 ( h i , r j , t x ) (h_i, r_j, t_x) (hi,rj,tx)的评分。这样,经过训练的实体和关系嵌入在KG中可以保持真实三元的内在语义。我们主要可以划分现有的KGE方法分为两类。第一类是基于距离(DB)的方法,使用闵可夫斯基距离作为评分函数来衡量三重的可信度,包括TransE (Bordes et al 2013), TransH (Wang et al 2014), TransR (Lin et al 2015), TransD (Ji et al 2015)和TransG (Xiao, Huang, and Zhu 2016)。另一类是基于张量分解(TDB)的方法,该方法将知识图视为三阶二进制张量,并使用张量分解的结果作为实体和关系的表示。TDB方法包括CP (Hitchcock 1927), DistMult (Yang et al 2015), RESCAL (Nickel, Tresp, and Kriegel 2011)和ComplEx (Trouillon et al 2016)。
- 但是,以往的方法忽略了不同三元组中相关实体和实体-关系对之间的联系。他们分别将每个三重输入到评分函数中,并优化评分函数的输出,以学习实体和关系的嵌入。在知识图中,具有相同实体-关系对(实体)的一些实体(实体-关系对)具有相似的语义。捕获这些实体或对的语义相似性可以提高嵌入的表达性,这表明在捕获语义信息方面的性能(Dettmers et al 2018;Xu et al 2020)。例如,在图1 (a)中,实体New York和Los Angeles共享相同的实体-关系对(City of, United States)。因此,实体纽约和洛杉矶应该有类似的嵌入。此外,在图1 ©中,夫妻(New York, City of)和(Washington, d.c., Captical of)共享同一个尾实体United States,这两对夫妻的表示也应该相似。

- 为了关联不同三元组中的相关实体和实体-关系对,我们提出了一种简单而有效的知识图嵌入对比学习框架,称为KGE- cl,它是现有KGE方法的通用框架。我们首先为具有相同实体-关系对的实体和具有相同实体-关系对的实体构造积极实例。例如,图1 (b)中Beau Biden的正面实例是Hunter Biden,图1 (d)中(Children, Beau Biden)的正面实例是(Spouse, Jill Biden)。然后计算原始实例和正实例的对比损失。由于对比学习框架的设计,我们也可以增加不相关的实体和夫妻之间的距离。最后,由于每个triple有4个正实例(对应图1中的4个例子),我们设计了加权对比损失,灵活控制不同正实例损失的权重。
- 我们使用标准WN18RR (Toutanova和Chen 2015)、FB15k-237 (Dettmers等人2018)和YAGO310 (Mahdisoltani, Biega和Suchanek 2015)数据集评估我们在KG链路预测任务上的kg- cl方法。我们提出的方法获得了最新的结果(SotA),在WN18RR数据集上获得了51.2%的MRR, 46.8%的Hits@1,在YAGO3-10数据集上获得了59.1%的MRR, 51.8%的Hits@1。此外,在不同关系的三元组上,我们将我们的方法与基线进行比较,进一步分析了改进。最后,为了清楚地解释我们的方法优于现有方法的原因,我们使用T-SNE (van der Maaten and Hinton 2008)对我们的方法和一些比较方法的知识图嵌入进行了可视化。
- 总之,本文的贡献包括:
- 我们提出了KGE-CL,一个简单而有效的知识图嵌入对比学习框架。它可以捕获不同三元组中相关实体和实体-关系对的语义相似度,从而提高嵌入的表达性。据我们所知,KGE-CL是第一个知识图嵌入的对比学习框架。
- 我们提出的KGE-CL框架还可以在语义空间中将不相关实体和对的嵌入分开。
- 实验结果和分析证实了KGE-CL方法的有效性.
相关工作
- 近年来,知识图嵌入(KGE)在各种下游应用中发挥着重要作用,成为研究的热点。我们可以将现有的KGE技术分为两类:基于距离的KGE方法和基于张量分解的KGE方法。
- 基于距离(DB)的方法将关系描述为头部和尾部实体之间的关系映射。他们通常使用闵可夫斯基距离来为给定的三连音打分。TransE是一种具有代表性的基于距离的方法,它使用关系作为翻译,其评分函数为:f(hi, rj, tk) =−||hi + rj−tk||22。为了提高TransE的性能,许多遵循相同方向的TransH变体被提出,例如TransH (Wang et al 2014), TransR (Lin et al 2015), TransD (Ji et al 2015), TranSparse (Ji et al 2016), TransG (Xiao, Huang, and Zhu 2016)。结构化嵌入(SE) (Bordes et al 2011)将这些关系作为头尾实体上的线性映射,其评分函数为:f(hi, rj, tk) =−kR1jhi−R2jtkk1。RotatE (Sun et al 2019)使用每个关系作为复向量空间中的旋转,其评分函数由:f(hi, rj, tk) =−khi◦rj−tkk1,其中hi, rj, tk∈Ck, |[r]i| = 1。
- 基于张量分解(TDB)的KGE方法将KGE任务描述为一个三阶二元张量分解问题。RESCAL (Nickel, Tresp, and Kriegel 2011)将X的第j个正面切片分解为Xj≈ARjA>,其中头部和尾部实体的嵌入来自同一空间。由于RESCAL中的关系嵌入是包含大量参数的矩阵,因此RESCAL更容易过拟合,训练难度更大。DistMult (Yang et al 2015)将RESCAL中的矩阵Rj简化为对角矩阵,而RESCAL只能保持关系的对称性,限制了其表达性。为了对不对称关系建模,ComplEx (Trouillon et al 2016)将DistMult扩展到复杂嵌入,并保留关系的实部对称和虚部不对称。此外,QuatE (Zhang et al .2019)进一步将ComplEx扩展到超复空间,以建模更复杂的关系属性,如反演。所有的DistMult、ComplEx和QuatE都是CP分解的变体(Hitchcock 1927),它们分别在实向量空间、复向量空间和超复向量空间中。另一方面,TDB方法通常存在过拟合问题;因此,一些工作试图从正则化子方面改进TDB方法,如N3 (Lacroix, Usunier, and Obozinski 2018)和DURA (Zhang, Cai, and Wang 2020)正则化子。这些正则化器带来了比原来的平方Frobenius范数(L2范数)正则化器更显著的改进(Nickel, Tresp, and Kriegel 2011;杨杨等2015;Trouillon et al 2016)。
- 然而,现有的基于距离的方法和基于张量分解的方法都分别用评分函数对每个三元组进行优化,忽略了不同三元组中实体或实体-关系对之间的关系。因此,它们不能正确地捕获这些相关实体和不同三元组中的配对之间的语义相似性。为了解决现有工作的局限性,我们提出了学习知识图嵌入的KGE-CL方法。
背景
- 在本节中,我们将介绍Setcion 3.1中知识图嵌入的背景,以及章节3.2中对比学习的背景。
知识图谱嵌入
- 给定一个实体集E和一个关系集R,知识图K = {(hi, rj, tk)}是一个三元组集合,其中hi∈E是头实体,rj∈R是关系,tk∈E是尾实体。
- 知识图嵌入(KGE)知识图嵌入(KGE)是学习实体和关系的表示(可以是实向量,也可以是复向量,矩阵和张量)。它的目标是学习到的实体和关系嵌入能够保留知识图中三元组的语义信息。通常,KGE方法定义了一个评分函数(hi, rj, tk)来对对应的三元组(hi, rj, tk)进行评分,该评分衡量三元组的可信度。现有的KGE工作包含两个重要的类别:基于距离的方法和基于张量分解的方法。
- DB方法定义评分函数f(hi, rj, tk)与Minkowski距离(Bordes et al 2013;Wang et al 2014;Lin et al 2015;Ji等2015;Xiao, Huang, and Zhu 2016),这类方法的评分函数为:f(hi, rj, tk) =−kΓ(hi, rj, tk)kp,其中Γ为模型特定函数。
- 基于张量分解(TDB)的KGE方法RESCAL (Nickel, Tresp, and Kriegel 2011)和ComplEx (Trouillon et al 2016)等TDB方法将知识图视为三阶二元张量 X ∈ { 0 , 1 } ∣ E ∣ × ∣ R ∣ × ∣ E ∣ X∈\{ 0,1\} ^{|E|×|R|×|E|} X∈{0,1}∣E∣×∣R∣×∣E∣。 ( i , j , k ) (i, j, k) (i,j,k)项 X i j k = 1 X_{ijk} = 1 Xijk=1,如果 ( h i , r j , t k ) (h_i, r_j, t_k) (hi,rj,tk)是一个真三元组,否则 X i j k = 0 X_{ijk} = 0 Xijk=0。 X j X_j Xj表示 X X X的第 j j j个正面切片,即第 j j j个关系对应的矩阵。通常,TDB KGE模型将 X j X_j Xj分解为 X j ≈ R e ( H R j T T ) X_j≈Re (HR_jT^T) Xj≈Re(HRjTT),其中H (T)的第i (k)行为hi (tk), Rj为表示关系Rj的矩阵,Re(·)和·分别为复矩阵的实部和共轭。那么TDB KGE方法的评分函数为:f(hi, rj, tk) = Re (hiRjt> k)。注意实矩阵的实部和共轭就是它本身。TDB模型的目标是寻找矩阵H, R1,…R|R|, T,使得Re (HRjT>)可以近似Xj。在本文中,我们的目标是改进现有的TDB模型,如RESCAL和ComplEx模型的性能。
对比学习
- 对比学习是一种有效的表示学习方法,将积极对与消极对进行对比(Hadsell, Chopra, and LeCun 2006;He et al 2020;Chen et al 2020;Khosla et al 2020)。对比学习的关键思想是把语义上接近的对拉到一起,把消极的对推开。无监督对比学习框架(Chen et al 2020)将利用数据增强构建正对来计算对比损失。有监督的对比学习框架(Khosla et al 2020)计算同一迷你批内所有正实例的对比损失。在这些现有框架的激励下,我们采用以下函数来计算实例 z i z_i zi与其所有正实例 z i + z_i^+ zi+之间的对比损失:
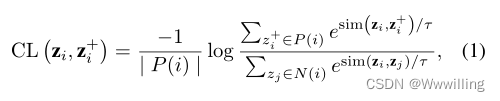
- 其中 z i z_i zi和 z i + z^+_i zi+分别表示zi和zi+ 。 P ( i ) P (i) P(i)是小批中所有正实例的集合, N ( i ) N(i) N(i)是批中所有负实例的集合。我们将消极实例定义为不属于积极实例的实例。 S i m ( z i , z i + ) = z i ⋅ z i + Sim (z_i, z^+_i) = z_i·z^+_i Sim(zi,zi+)=zi⋅zi+点积相似度。
我们的方法:KGE-CL
- 在本节中,我们描述了我们的KGE-CL方法,该方法利用对比学习来捕获不同三元组中相关实体和对的语义相似性。我们的方法是非常普遍的,可以很容易地应用到任意张量分解的方法。当我们使用RESCAL或ComplEx模型的评分函数时,我们可以进一步将KGECL方法命名为RESCAL- cl或ComplEx- cl。在本节中,我们首先介绍了我们为知识图嵌入设计的对比损失,然后介绍了我们的方法的训练目标。
知识图嵌入的对比损失
- 在本小节中,我们将详细介绍为知识图嵌入设计的对比损耗。
- 正样本:在对比学习中,为实例 z i z_i zi生成积极实例 z i + z^+_i zi+是至关重要的。视觉表征学习的现有工作(Wu et al 2018;Chen et al 2020;Chen and He 2020)使用了一些数据增强方法,如裁剪、颜色失真和旋转,对相同的图像进行两次随机变换,如 z i z_i zi和 z i + z^+_i zi+。同时,在NLP中,一些工作(Wu et al 2020;孟等人2021)利用了其他增强技术,如单词删除、重新排序和替换。然而,这些数据增强方法并不适用于知识图嵌入。为了获取知识图中三元组之间的相互作用,我们设计了一种构建知识图嵌入正实例的新方法。对于三元组 ( h i , r j , t k ) (h_i, r_j, t_k) (hi,rj,tk), TDB方法对应的计分函数为:
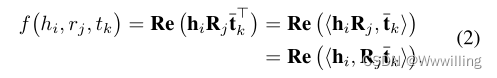
- 我们定义 < ⋅ , ⋅ > <·,·> <⋅,⋅>为两个实向量或复向量的内积: < u , v > = u v T <u, v>= uv^T <u,v>=uvT。 h i R j h_iR_j hiRj和Rjtk分别是实体-关系对(hi, rj)和(rj, tk)的表示。式2表示我们可以先计算评分函数中的hiRj或Rjtk。对于一个头部实体hi,我们将其正实例h+ i定义为那些与hi共享相同关系和尾部实体的头部实体。类似地,我们将尾部实体tk的正实例t+ k定义为那些与tk共享相同头部实体和关系的尾部实体。对于实体-关系偶(hi, rj)或(rj, tk),对应的正实例(hi, rj)+或(rj, tk)+是与(hi, rj)或与(rj, tk)具有相同尾部实体或头部实体的实体-关系偶。(hiRj)+和(Rjtk)+分别是正实例(hi, rj)+和(rj, tk)+的表示。因此,给定一个真三重(hi, rj, tk),我们的方法将构造四种正实例:h+ i, t+ k, (hi, rj)+和(rj, tk)+,它们对应于图1中的四个例子。对于实例hi,我们将在同一个迷你批处理中使用它的所有正实例h+ i。
- 在现有的对比学习框架的激励下,我们利用一个基编码器g(·)对四种类型的正对(hi, h+ i), (tk, t+ k), ((hi, rj), (hi, rj)+)和(rj, tk), (rj, tk)+)中的原始和正实例进行编码。我们使用的基编码器g(·)是一个2层MLP,它在每个隐层中都有一个批量归一化(Ioffe and Szegedy 2015)和一个ReLU激活函数。为了使表示法更方便和清晰,我们使用相同的表示法来表示编码器的输出,例如hi = g?hi ?, (hiRj)+ = g?(hiRj)+?
- 给定一个真三重
(
h
i
,
r
j
,
t
k
)
(h_i, r_j, t_k)
(hi,rj,tk),我们用公式1计算四种正实例输入基编码器后的对比损失,一个三重(hi, rj, tk)的总体对比损失为:
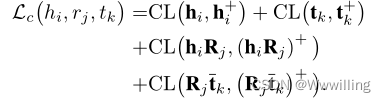
- 我们从梯度的角度分析式3。取对比损失项CL ?hi, h+ i ?例如,CL ?hi, h+ i ?对嵌入hi是:
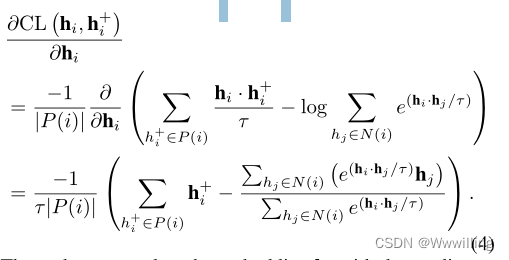
- 然后,当我们用梯度更新嵌入hi时:
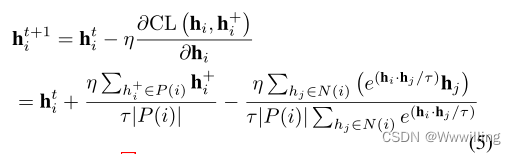







![[数据结构]:09-二分查找(顺序表指针实现形式)(C语言实现)](https://img-blog.csdnimg.cn/4da1fbe0a8354b3592515519f873c81d.png)