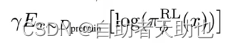如果觉得我的分享有一定帮助,欢迎关注我的微信公众号 “码农的科研笔记”,了解更多我的算法和代码学习总结记录。或者点击链接扫码关注【2023/图对比/无负样本】基于无负样本损失和自适应增强的图对比学习
周天琪,杨艳,张继杰等.基于无负样本损失和自适应增强的图对比学习[J/OL].浙江大学学报(工学版):1-8[2023-02-27]
1 动机
图对比学习方法中对输入图进行随机增强和须利用负样本构造损失的问题,提出基于无负样本损失和自适应增强的图对比学习框架。现实世界中获得有标签的图信息的代价是昂贵的,针对这一问题,自监督学习(self-supervised learning, SSL)范式为图表示学习提供了一种可行的解决方法。最典型的是对比学习. 对比学习通过最大化正样本对之间的一致性和负样本对之间的不一致性来学习特征编码器。目前,CV领域已经有相关工作解决了需要负样本的问题,例如BGRL、Bar-low Twings、孪生网络架构等。作者直接提出无负样本损失和自适应增强对比学习,典型将自适应数据增强域Barlow Twins损失函数结合。
2 方法
该框架计算一个图的 2 个变体视图的嵌入互相关矩阵,所采用的网络结构是完全对称的。
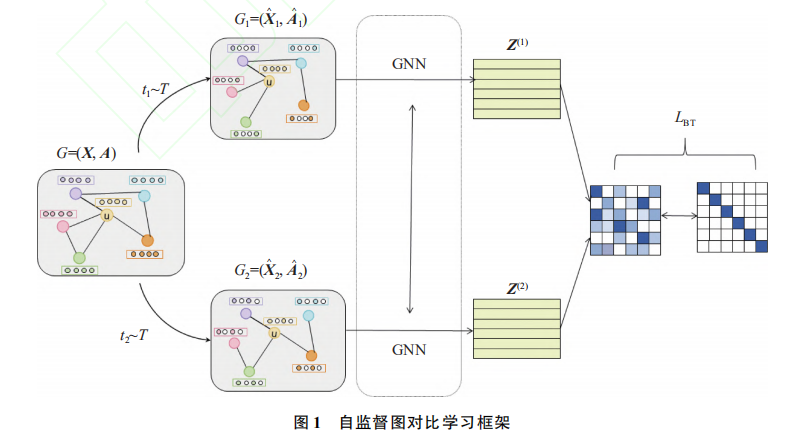
2.1【生成视图进行自适应增强】
本研究设计的增强方案是量化节点间重要性,即保存重要性高的结构和属性不变,对重要性低的边和特征信息进行扰动。之前很多是随机进行,这样会对数据增强产生不利的影响。作者利用数据增强生成2个增强视图,包括改变图的结构和属性2个方面。
- 结构方面:利用节点度中心性计算边的中心性,根据得到的边的重要性,以一定概率删除不重要的边。
- 属性方面:在属性方面,通过将属性向量中不重要的维度替换为 0,掩盖节点属性信息
2.2 【无负样本对比loss】
组会-当下热门的深度自监督学习(基于正则化) https://www.bilibili.com/video/BV1t3411M7eT/
代码:https://github.com/facebookresearch/barlowtwins
Barlow Twins 损失函数是一种用于自监督学习的损失函数,由 Google Brain 团队的 Jure Zbontar 和 Li Jing 在 2021 年提出。该损失函数的主要目的是学习图像的特征表示,其关键思想是通过学习两个不同但相关的特征映射之间的相关性来优化网络参数。具体而言,Barlow Twins 损失函数利用了两个特征映射的 Gram 矩阵之间的相关性来衡量它们之间的相似度。Gram 矩阵是指由特征映射中的各个通道之间的内积组成的矩阵,可以看作是一种度量特征之间相关性的方式。因此,Barlow Twins 损失函数的核心思想是最小化两个特征映射的 Gram 矩阵之间的差异。Barlow Twins损失函数不依赖非对称神经网络架构。
具体而言,Barlow Twins 损失函数可以表示为:
L
B
T
≜
∑
i
(
1
−
C
i
i
)
2
⏟
invariance term
+
λ
∑
i
∑
j
≠
i
C
i
j
2
⏟
redundancy redustition terinps
\mathcal{L}_{\mathcal{B} \mathcal{T}} \triangleq \underbrace{\sum_{i}\left(1-\mathcal{C}_{i i}\right)^{2}}_{\text {invariance term }}+\lambda \underbrace{\sum_{i} \sum_{j \neq i} \mathcal{C}_{i j}^{2}}_{\text {redundancy redustition terinps }}
LBT≜invariance term
i∑(1−Cii)2+λredundancy redustition terinps
i∑j=i∑Cij2
其中
λ
\lambda
λ 是一个正常数,用来权衡两项之间的重要性,
C
C
C 是两个相同网络输出embeedings之间计算得到的互相关矩阵:
C
i
j
≜
∑
b
z
b
,
i
A
z
b
,
j
B
∑
b
(
z
b
,
i
A
)
2
∑
b
(
z
b
,
j
B
)
2
\mathcal{C}_{i j} \triangleq \frac{\sum_{b} z_{b, i}^{A} z_{b, j}^{B}}{\sqrt{\sum_{b}\left(z_{b, i}^{A}\right)^{2}} \sqrt{\sum_{b}\left(z_{b, j}^{B}\right)^{2}}}
Cij≜∑b(zb,iA)2∑b(zb,jB)2∑bzb,iAzb,jB
互相关矩阵其中,
b
b
b 索引batch内样本,
i
,
j
i,j
i,j 索引网络输出的向量维度。
C
C
C 是一个方阵,大小为网络输出的维数,他的值介于-1 (完全负相关) 和 1 (完全相关) 之间。
实践代码如下所示:
- 假设sizes[-1]等于128,batch size等于64,每个输入图像的大小为3x32x32,我们可以用一个4层卷积神经网络作为backbone,并将其输出嵌入到128维空间中。这将得到两个形状为(64, 128)的矩阵z1和z2。
- 现在,我们将这两个矩阵传递给BatchNorm1d层,该层将对它们进行标准化处理。具体来说,对于每个特征通道,它会减去均值并除以方差。这将产生两个标准化的形状为(64, 128)的矩阵。
- 然后,我们将z1的转置和z2相乘,得到一个(128, 128)的交叉相关矩阵c。
我们将这个交叉相关矩阵除以batch size,然后使用all_reduce函数将它们在多个GPU之间求和。 - 接下来,我们计算对角线元素和非对角线元素的损失值。其中,对角线元素代表两个输入中相同的特征之间的相似度,而非对角线元素代表不同的特征之间的相似度。通过计算对角线元素减1的平方和来强制鼓励同类之间的相似度。通过计算非对角线元素的平方和来强制鼓励异类之间的不同。
- 最后,将这两个损失相加以得到最终的损失值。
# normalization layer for the representations z1 and z2
self.bn = nn.BatchNorm1d(sizes[-1], affine=False)
def off_diagonal(x):
# return a flattened view of the off-diagonal elements of a square matrix
n, m = x.shape
assert n == m
return x.flatten()[:-1].view(n - 1, n + 1)[:, 1:].flatten()
def forward(self, y1, y2):
z1 = self.projector(self.backbone(y1))
z2 = self.projector(self.backbone(y2))
# empirical cross-correlation matrix
c = self.bn(z1).T @ self.bn(z2)
# sum the cross-correlation matrix between all gpus
c.div_(self.args.batch_size)#将张量 c 中的所有元素都除以 self.args.batch_size,并将结果存回到张量 c 中。
torch.distributed.all_reduce(c) #在分布式深度学习中,所有计算节点需要对梯度进行聚合操作以更新模型权重。all_reduce 操作可以将梯度从所有节点中收集并相加,以便在所有节点上计算相同的梯度更新。这有助于确保在所有节点上训练的模型参数保持同步。
on_diag = torch.diagonal(c).add_(-1).pow_(2).sum()
off_diag = off_diagonal(c).pow_(2).sum()
loss = on_diag + self.args.lambd * off_diag
return loss
3 总结
移花接木idea有了