算法设计与分析期末考试复习（五）

回溯法

回溯法是一种试探法，将n元问题P的状态空间E表示成为一棵高为n的带权有序数T，把在E中求问题P的解转换为在T中搜索问题P的解。
解题方法：按选优条件对T进行深度优先搜索，以达到目标。

从根节点出发深度优先搜索解空间树。
当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续按深度优先策略搜索，否则逐层向其祖先结点回溯（退回一步重新选择），满足回溯条件的某个状态的点称为“回溯点”。

算法结束条件：

求所有解：回溯到根，且根的所有子树均搜索完成。
求任一解：只要搜索到问题的一个解就可以结束。

问题的解空间
应用回溯法解题时，首先应明确问题的解空间，问题的解空间应至少包含该问题的一个解。
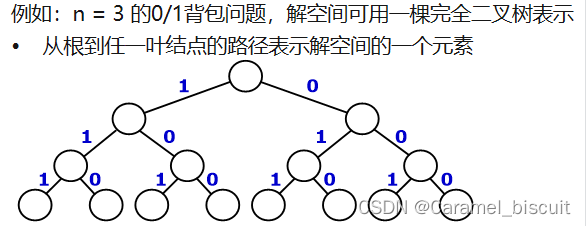
在这里插入图片描述

扩展结点：一个正在产生子结点的结点称为扩展结点。
活结点：一个自身已生成但其子结点尚未全部生成的结点。
死结点：一个所有子结点已经产生的结点。

深度优先的问题状态生成法
对于一个扩展结点R，一旦产生了它的一个子结点C

则将其作为新扩展结点，并对以C为根的子树进行穷尽搜索。
在完成对子树C的穷尽搜索后，将R重新变成扩展结点。
继续生成R的下一个结点，若存在，则对其进行穷尽搜索。

宽度优先的问题状态生成法
在一个扩展结点变成死结点之前，它一直是扩展结点。

回溯法的解题思路

从根节点开始深度优先搜索解空间（利用剪枝避免无效搜索），此时根节点成为活结点，并成为当前的扩展结点。
进一步地搜索从当前扩展结点开始，向纵深方向移至一个新结点，该新结点成为新的活结点，并成为当前扩展结点。
若在当前扩展结点出不能再向纵深方向移动，则当前扩展结点变为死结点，此时应回溯至最近的活结点，将其作为当前扩展结点。
直到找到所要求的解，或者解空间中已经没有活结点为止。

通用算法框架

void backtrack(int t){
	if(t > n){
		output(x);
	}else{
		for(int i=f(n,t); i<=g(n,t); i++){ //f(n,t)表示当前扩展结点处为搜索过的子树的起始编号，g(n,t)当前扩展结点处未搜索到过的子树的终止编号
			x[t] = h(i); //h(i)表示当前扩展节点处x[t]的第i个可选值
			if(constraint(t) && bount(t)){
				backtrack(t+1);
			}
		}
	}
}

两类常见的解空间树

用回溯法解题时常用到两种典型的解空间树：子集树与排列树。
子集树

当问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树，例如n个物品的0/1背包问题。
这类子集树通常有2ⁿ个叶节点。
解空间树的结点总数为 2ⁿ⁺¹-1
遍历子集树的算法需Ω(2ⁿ)计算时间

排列树

当问题是：确定n个元素满足某种性质的排列时。相应的解空间树称为排列树，例如旅行商问题。
排列树通常有n!个叶节点。
因此遍历排列树需要Ω(n!)计算时间

子集树示例： 0/1背包问题
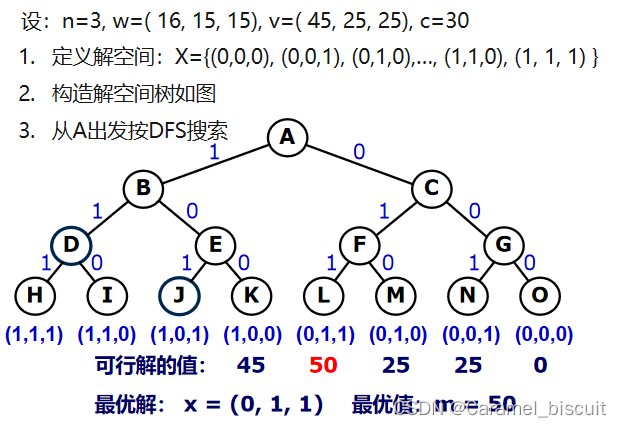
在这里插入图片描述
子集树回溯算法框架

void backtrack(int t){
	if(t > n){
		output(x);
	}else{
		for(int i=0; i<=1; i++){
			x[t] = i;
			if(constraint(t)&&bound(t)){
				backtrack(t+1);
			}
		}
	}
}

排列生成问题
问题定义：给定正整数n，要求生成1, 2, …, n的所有排列.
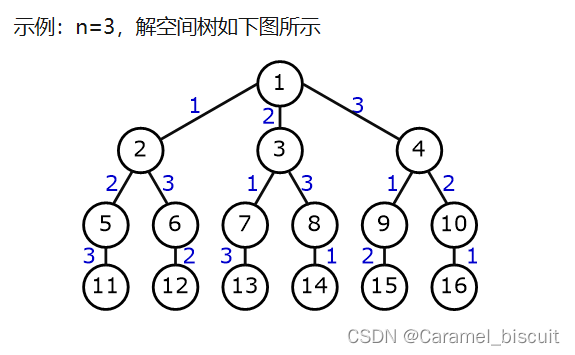
在这里插入图片描述
排列树回溯算法框架

void backtrack(int t){
	if(t > n){
		output(x);
	}else{
		for(int i=t; i<=n; i++){
			swap(x[t],x[i]);
			if(constraint(t) && bound(t)){
				backtrack(t+1);
			}
			swap(x[t],x[i]);
		}
	}
}

回溯法显著特征是在搜索过程中动态产生问题的解空间，在任何时刻，算法只保存从根节点到当前扩展结点的路径。

如果解空间树从根节点到叶节点的最长路径为h(n)，则回溯法所需的内存空间通常为h(n)。

常用剪枝函数

约束函数：在扩展结点处减去不满足约束的子树。显示约束：对分量xi的取值范围限制。隐式约束：为满足问题的解而对不同分量之间施加的约束。
限界函数：减去得不到最优解的子树。

NP完全性问题

优化问题（也称为极值问题）

实例集合：若干实例I组成集合D，其中每一个实例I含有一个问题所有输入的数据信息。
可行解：每一个实例I有一个解集和S(I)，其中的每一个解都满足问题的条件，称为可行解。
目标函数：映射c(σ): S(I)→ℜ
最优化：求最优解 σopt (I) ∈S(I)，使得对任意一个可行解σ∈S(I)，都有c(σopt (I)) ≥c(σ) 或者c(σopt (I)) ≤c(σ)

一个优化问题也可以视为一个判定问题
判定问题（也称为识别问题）

仅有两种可能的答案：“是”或者“否”
可以将一个判定问题视为一个函数，它将问题的输入集合I映射到问题解的集合{0 1}
以路径判断问题为例：给定一个图G=(V, E) 和顶点集V中的两个顶点u, v，判断 G 中是否存在一条路u和v之间的路，如果用 i=<G, u, v>表示该问题的一个输入，则：函数PATH(i)=1 （当u和v之间存在一条路时），则：函数PATH(i)=0 （当u和v之间不存在一条路时）

P和NP都是问题的集合

P是所有可在多项式时间内用确定算法求解的判定问题的集合，对于一个问题X，若存在一个算法XSolver，能在O(nk)时间内求解（k为某个常数），那么就称这个问题属于P
NP是所有可用多项式时间算法验证其猜测准确性的问题的集合，对于一个问题X，若存在一个算法XChecker，能在多项式时间复杂度内给出验证结果，那么就称这个问题属于NP

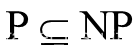
NP-Complete(NPC NP完全问题)
如果一个问题属于NP，且该问题与NP中的任何问题是一样难（hard）的，则称该问题属于NPC，或称之为NP完全的（ NP-Complete ）。
如果任何一个NPC问题可以在多项式时间内解决，则NP中的所有问题都有一个多项式时间的算法

如何证明一个问题属于NPC类

NP完全性只适用于判定问题
NP完全性的定义和证明方法
第一个NP完全问题：电路可满足性问题

一些经典的NP问题

在这里插入图片描述
判定问题A是NP完全的

A属于NP类
NP中的任何问题均可在多项式时间内规约到A。

旅行商问题

某推销员要去若干城市推销商品，已知各城市间的开销（路程或旅费），要求选择一条从驻地出发，经过每个城市一遍，最后回到驻地的路线，使总开销最小。
这是一个NP完全问题，形式化描述如下：

给定带权图G=(V,E)，已知边的权重为正数。
图中的每一条周游路线是包括V中每个顶点的一条回路。
一条周游路线的开销是这条路线上所有边的权重之和
要求在图G中找出一条具有最小开销的周游路线

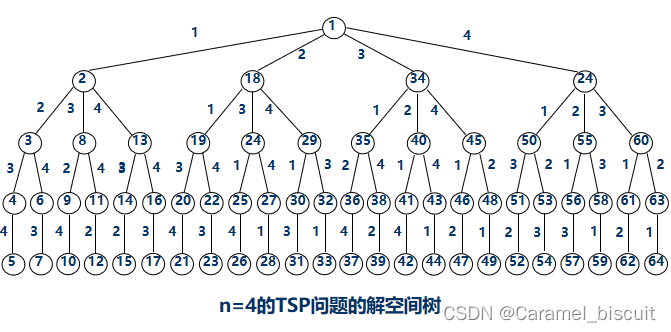
对于n=4的TSP问题，其解空间树如图所示，树中的4！=24个叶子结点代表该问题的24个可能解。
与排列问题相比，多了一个回路。
基本思想：利用排列生成问题的回溯算法Backtrack()，Backtrack(2)表示：对x[2:n]进行全排列。
则(x[1], x[2])，(x[2], x[3])，…, (x[n], x[1])构成回路
在全排列算法的基础上，进行路径计算保存以及限界剪枝

void main(){
	//输入邻接矩阵A[n][n]
	x[n]= {1,2,..,n};
	sum = 0; //记录最短路径和
	S[n] = {0}; //保存当前最佳路径
	m = ∞; // m保存当前最优值
	backtrack(2,S,m,&sum);
	output(m,s)
}

解空间：X={12341, 12431, 13241, 13421, 14231, 14321}
解空间树中的每个叶结点恰好对应于图G的每一条周游路线，解空间树中的叶结点个数为(n-1)!

void backtrack(int i){
	if(i > n){ //输出可行解，与当前最优解比较
		if(sum+A[x[n]][x[1]]<m || m=∞){
			m = sum + A[x[n]][x[1]];
			for(k=1; k<=n; k++){
				S[k] = x[k];
			}
		}
	}else{
		for(k=i; k<=m; k++){
			if(sum+A[x[i-1]][x[k]]<m || m = ∞){
				swap(x[i],x[k]);
				sum = sum + A[x[i-1]][x[k]];
				backtrack(i+1);
				sum = sum-A[x[i+1]][x[k]];
				swap(x[i],x[k]);
			}
		}
	}
}//初始调用backtrack(2)

0/1背包问题

怎样计算价值上界？
例：n = 4，c = 7，p = [9, 10, 7, 4]，w = [3, 5, 2, 1]

易求得这四个物品的单位重量价值分别为：[3,2,3.5,4]
按物品单位重量价值递减的顺序装入物品
依次装入物品4、3、1，剩余背包容量为1
所以只能容纳物品2的20%
得到的解向量x=[1,0.2,1,1]，相应价值为22
虽然x并不是0/1背包问题的可行解，但它提供了一个最优的价值上界（最优值不超过22）
为便于计算上界函数，可先对物品按单位价值从大到小排序
对每个扩展结点，只需按顺序考查排在其后的物品即可

int Bound(int i){
	int wr = c-wc; //背包剩余容量
	int vb = vc; //vc当前背包价值
	while(i<=n && w[i]<=wr){
		wr -= w[i];
		vb += v[i];
		i++;
	}
	if(i<=n){
		vb += (v[i]/w[i])*wr;
	}
	return vb;
}

void backtrack(int i){
	if(i > n){
		m = (m < vc)?vc:m;
		output(x);
	}else{
		if(wc+w[i] <= C){ //左子树，将i放入背包
			x[i] = 1;
			wc += w[i];
			vc += v[i];
			backtrack(i+1);
			x[i] = 0;
			wc -= w[i];
			vc -= v[i];
		}
		if(Bound(i+1) > m){ 右子树，拿出物品i
			x[i] = 0;
			backtrack(i+1);
		}
	}
}

装载问题

有n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi。
**装载问题要求：确定是否有一个合理的装载方案可将这n个集装箱装上这2艘轮船？如果有，找出一种装载方案。
**

示例：n=3，c1=c2=50
若：w=[10, 40, 40]
则可以将集装箱1和2装到第一艘船上
将3号集装箱装到第二艘船上
若：w=[20,40,40]
则无法将这三个集装箱全部装船

一艘船的情况，采用贪心选择策略：从轻到重依次装船，直至超重
目前有两艘船，首先将第一艘轮船尽可能装满，将剩余的集装箱装上第二艘轮船
将第一艘轮船尽可能装满，等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近c1，由此可知，装载问题等价于特殊的0-1背包问题。

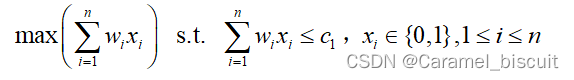
算法设计：用回溯法求解最优装载问题
解空间的表达：子集树
约束函数：
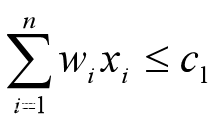
在子集树的第k层的结点R处，以ck表示当前的装载重量。
当ck>c1时，以结点R为根的子树中所有结点均不满足约束条件，因而该子树中的解均为不可行解，故可将该子树剪去。
限界函数（用于剪去不含最优解的子树）
设R是解空间树第k层上的当前扩展结点。
wc表示当前结点对应的的装载重量
wm表示当前的最优载重量
wr表示剩余集装箱的重量
定义限界函数w = wc+wr
以R为根的子树中任一叶节点对应的载重量均不会超过w
因此当 w≤wm 时，可将以R为根的子树剪去

void backtrack(int i){
	if(i > n){
		if(wc > wm){
			wm = wc;
			return;
		}
	}
	wr -= w[i];
	if(wc + w[i] <= C){ //搜索子树
		x[i] = 1;
		wc += w[i];
		backtrack(i+1);
		wc -= w[i];
		x[i] = 0;
	}
	if(wc + wr >wm){ //搜索右子树
		 x[i] = 0;
		 backtrack(i+1);
	}
	wr += w[i];
}

n-皇后问题

皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子，在n×n的棋盘上放置彼此不受攻击的n个皇后，即：任何2个皇后不放在同一行或同一列或同一斜线上

问题的解向量：(x1, x2, … , xn)
采用数组下标 i 表示皇后所在的行号
采用数组元素x[i]表示皇后 i 的列号
排列树

剪枝函数

显约束（对解向量的直接约束）：xi = 1,2,…,n
隐约束：任意两个皇后不同列，xi!=xj
隐约束：任意两个皇后不处于同一对角线|i-j|≠|xi-xj|

bool Bound(int k){
	for(int i=0; i<k; i++){
		if((abs(k-i)==abs(x[k]-x[i])) || x[k]==x[i]){
			return false;
		}
	}
	return true;
}

void backtrack(int t){
	if(t>n){
		output(x);
	}else{
		for(int i=0; i<n; i++){
			x[t] = i;
			if(Bound(t)){
				Backtrack(t+1);
			}
		}
	}
}

四皇后问题
四皇后问题的解空间树是一个完全4叉树，树的根节点表示搜索的初始状态，从根节点到第1层结点代表皇后1放在棋盘中第0行的可能摆放位置，从第1层结点到第2层结点对应皇后2在棋盘中第1行的可能摆放位置，以此类推。
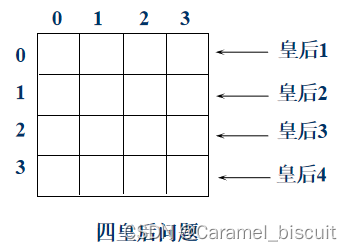
在这里插入图片描述
一般称用于确定n个元素的排列满足某些性质的解空间树为排列树，排列树有n!个叶子结点，遍历排列树的时间为O(n!)

最大团问题

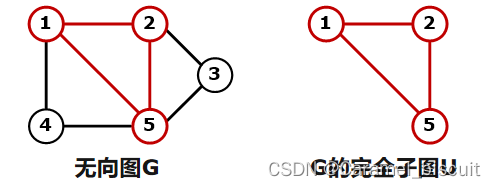
在这里插入图片描述
给定无向图G=(V,E)和G的完全子图。
完全子图： UV且对任意u∈U和v∈U，有(u，v) ∈ E

定义U是G的团，当且仅当U不包含在G的更大的完全子图中。
G的最大团是指：G中所含顶点数最多的团
子集{1,2}是图G的大小为2的完全子图，但不是一个团，因为它包含在G的更大的完全子图{1,2,5}之中
子集{1,4,5}和{2,3,5}也是G的最大团

无向图的补图

无向图G=(V，E)的补图G’=(V’，E’) 定义为V’=V，且(u，v)E’ 当且仅当 (u，v) E
显然：补图的概念是相对于完全图定义的

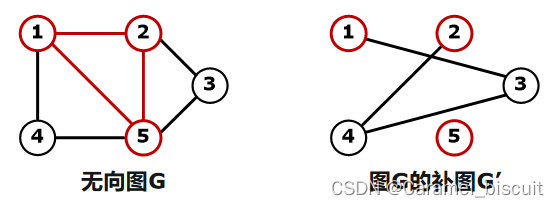
在这里插入图片描述

最大独立集

如果UV且对任意u，v∈U有(u，v)E，则称U是G的空子图
空子图U是G的独立集当且仅当U不包含在G的更大的空子图中。
G的最大独立集：G中所含顶点数最多的独立集

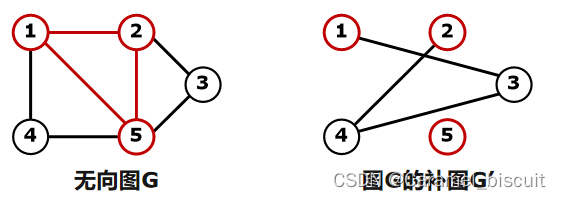
在这里插入图片描述

{2,4}是G的一个空子图，同时也是G的一个最大独立集
子集{1,2}是G’的空子图，但它不是G’的独立集，但它不是独立集，因为它包含在G’的空子图{1,2,5}中
子集{1,2,5}是G’的最大独立集
子集{1,4,5}和{2,3,5}也是G’的最大独立集

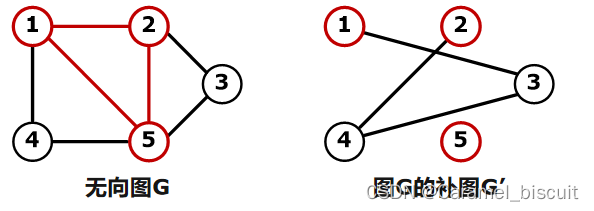
在这里插入图片描述

无向图G的最大团和最大独立集问题是等价的
U是G的完全子图，则它也是G’的空子图，反之亦然
U是G的最大团当且仅当U是G’的最大独立集
二者都可以看做是图G的顶点集V的子集选取问题，二者都可以用回溯法在O(n2ⁿ)的时间内解决

最大团问题
问题的解向量：（x1,x2,x3,…,xn）为0/1向量：xi 表示该顶点是否入选最大团。
解空间树采用子集树

解题思路

首先设最大团U为空集，向其中加入一个顶点v0.
然后依次考查其它顶点vi.
若vi加入后，U不再是团，则舍弃顶点vi(考查右子树)
若vi加入后，U仍是团？考虑将该点加入团或舍弃两种情况

剪枝函数
约束函数

新加入的顶点是否构成团
顶点vi到顶点集U中每一个顶点都有边相连
否则可对以vi为根的左子树进行剪枝

限界函数

当前扩展结点代表的团是否小于当前最优解
若剩余顶点数加上当前团中顶点数不大于当前最优解
则可以对vi为根的进行右子树剪枝

void backtrack(int i){
	int valid = 1;
	if(i > n){
		for(int k=1; k<=n; k++){
			m[k] = x[k];
		}
		mn = cn;// mn当前最大顶点数 cn当前顶点数
		return;
	}
	for(int k=1; k<i; k++){
		if(x[k] && G[i][k]==0){
			valid = 0;
			break;
		}
	}
	if(valid){ //满足约束条件，进入左子树
		cn++;
		x[i]=1;
		backtrack(i+1);
		x[i]=0;
		cn--;
	}
	if(cn+n-1 >= mn){ //满足限界条件，进入右子树
		x[i] = 0;
		backtrack(i+1);
	}
}

批处理作业调度问题

给定n个作业的集合{J1, J2, …, Jn}，每一个作业都有两项任务，需要分别在两台机器上完成，每个作业必须先由机器1处理，然后再由机器2处理，作业 Ji 需要机器 k 的处理时间为 tki (k=1,2)。
对于一个确定的作业调度，设：作业 Ji 在机器 k 上完成处理的时间为 Fki ，对给定的n个作业，制定作业调度方案，使其完成时间和最小。

问题的解向量：(x1, x2, … , xn)
数组元素 x[i] 表示该任务的调度顺序为 i
解空间树：排列树
当i<n时，当前扩展结点位于排列树的第i-1层，此时算法要选择下一个要安排的作业。
剪枝函数：若当前完成时间和大于已知的最优值，则剪去该子树。

void backtrack(int i){
	if(i > n){
		for(int k=1; k<=n; k++){
			mx[k] = x[k];
		}
		m = f;
	}else{
		for(int k=i; k<=n; k++){
			f1 += T[x[k]][1]; //机器1完成处理时间
			f2[i] = (f2[i-1]>f1)?(f2[i-1]:f1) + T[x[k]][2];
			f += f2[i];
			if(f < m){
				swap(x[i],x[k]);
				backtrack(i+1);
				swap(x[i],x[k]);
			}
			f1 -= T[x[k]][1];
			f -= f2[i];
		}
	}
}

图的m着色问题

数组元素x[i]表示顶点所着的颜色编号
采用子集树
问题的解空间可以表示为n+1的完全m叉树，每一层结点都有m个子节点，代表m种可能的颜色。
剪枝函数：为顶点i着色时，不能与已着色的相邻顶点颜色重复。

bool Bound(int k){//检查颜色可用性
	for(int i=1; i<=n; i++){
		if((G[k][i]==1)&&(x[i]==x[k]))
			return false;
	}
	return true;
}
void Backtrack(int t){
	if(t > n){
		output(x);
		sum++;
	}else{
		for(int i=1; i<=m; i++){
			x[t] = i;
			if(Bound(t)){
				Backtrack(t+1);
			}
		}
	}
}