深度优先/广度优先遍历

深度优先：

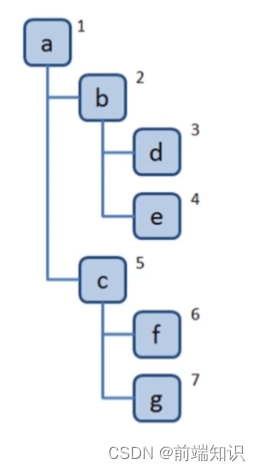
1. 访问根节点

2. 对根节点的 children 挨个进行深度优先遍历

const tree = {
  val: "a",
  children: [
    {
      val: "b",
      children: [
        {
          val: "d",
          children: [],
        },
        {
          val: "e",
          children: [],
        },
      ],
    },
    {
      val: "c",
      children: [
        {
          val: "f",
          children: [],
        },
        {
          val: "g",
          children: [],
        },
      ],
    },
  ],
};

const dfs = (root) => {
  console.log(root.val);
  root.children.forEach((child) => {
    dfs(child);
  });
};

dfs(tree);

广度优先：

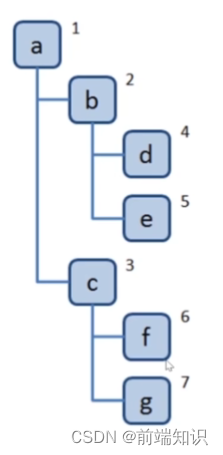
1. 新建立一个队列，根节点入队

2. 对头出队并访问

3. 把对头的children挨个入队

4. 重复2，3，直到队列为空

const tree = {
  val: "a",
  children: [
    {
      val: "b",
      children: [
        {
          val: "d",
          children: [],
        },
        {
          val: "e",
          children: [],
        },
      ],
    },
    {
      val: "c",
      children: [
        {
          val: "f",
          children: [],
        },
        {
          val: "g",
          children: [],
        },
      ],
    },
  ],
};

const bfs = (root) => {
  const q = [root];
  while (q.length > 0) {
    const n = q.shift();
    console.log(n.val);
    n.children.forEach((child) => {
      q.push(child);
    });
  }
};

bfs(tree);

二叉树的先中后序遍历

二叉树：每个节点最多只能有两个节点

先序遍历（根、左、右）：

1. 访问根节点

2. 对根节点的左子树进行先序遍历

3. 对根节点的右子树进行先序遍历

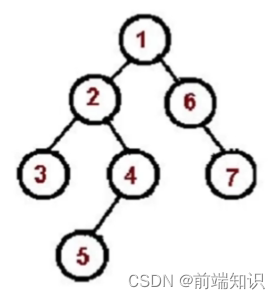
1、2、3、4、5、6、7

const tree = {
  val: "1",
  left: {
    val: "2",
    left: {
      val: "3",
      left: null,
      right: null,
    },
    right: {
      val: "4",
      left: {
        val: "5",
      },
      right: null,
    },
  },
  right: {
    val: "6",
    left: null,
    right: {
      val: "7",
      right: null,
      left: null,
    },
  },
};

const preorder = (root) => {
  if (!root) return;
  console.log(root.val);
  preorder(root.left);
  preorder(root.right);
};
preorder(tree);

中序遍历（左、中、右）：

1. 对根节点左子树遍历

2. 访问根节点

3. 对根节点右子树遍历

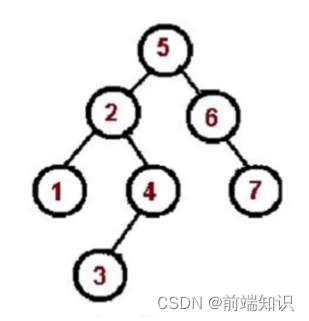
1、2、3、4、5、6、7

const tree = {
  val: "5",
  left: {
    val: "2",
    left: {
      val: "1",
      left: null,
      right: null,
    },
    right: {
      val: "4",
      left: {
        val: "3",
      },
      right: null,
    },
  },
  right: {
    val: "6",
    left: null,
    right: {
      val: "7",
      right: null,
      left: null,
    },
  },
};

const inorder = (root) => {
  if (!root) return;
  inorder(root.left);
  console.log(root.val);
  inorder(root.right);
};
inorder(tree);

后序遍历（左、右、根）：

1. 对根节点左子树遍历

2. 对根节点右子树遍历

3. 访问根节点

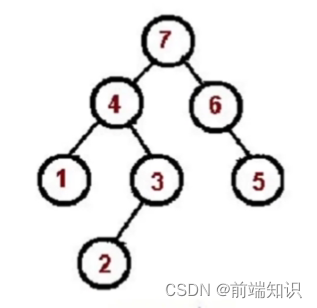
1、2、3、4、5、6、7

const tree = {
  val: "7",
  left: {
    val: "4",
    left: {
      val: "1",
      left: null,
      right: null,
    },
    right: {
      val: "3",
      left: {
        val: "2",
      },
      right: null,
    },
  },
  right: {
    val: "6",
    left: null,
    right: {
      val: "5",
      right: null,
      left: null,
    },
  },
};

const postorder = (root) => {
  if (!root) return;
  postorder(root.left);
  postorder(root.right);
  console.log(root.val);
};
postorder(tree);

非递归写法

递归调用函数，会不断的入栈出栈，所以考虑用栈实现。

先序遍历：

// 递归
const preorder = (root) => {
  if (!root) return;
  console.log(root.val);
  preorder(root.left);
  preorder(root.right);
};

// 非递归
const preorder = (root) => {
    if (!root) return;
    const stack = [root]
    while(stack.length){
        const n = stack.pop()
        console.log(n.val)
         // 栈后进先出，先右后左
        if(n.right) stack.push(n.right)
        if(n.left) stack.push(n.left)
    }
}

中序遍历：

// 递归
const inorder = (root) => {
  if (!root) return;
  inorder(root.left);
  console.log(root.val);
  inorder(root.right);
};
// 非递归
const inorder = (root) => {
  if (!root) return;
  const stack = [];
  let p = root;
  while (stack.length || p) {
    // 所有的左子树进栈
    while (p) {
      stack.push(p);
      p = p.left;
    }
    //最尽头的左子树出栈
    const n = stack.pop();
    console.log(n.val);
    p = n.right;
  }
};

后续遍历：

const postorder = (root) => {
  if (!root) return;
  postorder(root.left);
  postorder(root.right);
  console.log(root.val);
};
// 先序遍历是 根、左、右，后续遍历时：左、右、根，倒过来是根、右、左，只需要把先序遍历的后面两个颠倒顺序

const postorder = (root) => {
  if (!root) return;
  const outputStack = [];
  const stack = [root];
  while (stack.length) {
    const n = stack.pop();
    outputStack.push(n);
    if (n.left) stack.push(n.left);
    if (n.right) stack.push(n.right);
  }
  while (outputStack.length) {
    const n = outputStack.pop();
    console.log(n.val);
  }
};