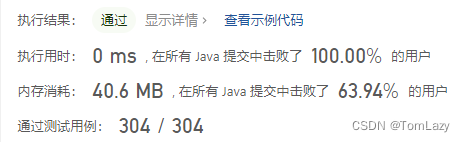
题目链接:https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/
1. 题目介绍(16. 数值的整数次方)
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。
【测试用例】:
示例 1:
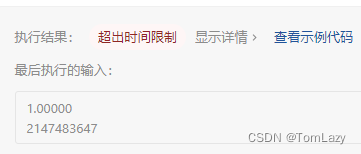
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
【条件约束】:
提示:
- -100.0 < x < 100.0
- -231 <= n <= 231-1
- -104 <= xn <= 104
【相同题目】:
注意:本题与主站 50. Pow(x, n) 题目相同.
2. 题解
2.1 对负指数次幂结果求倒数 – O(n)
时间复杂度O(n),空间复杂度O(1)
class Solution {
// 定义全局变量,用来提示函数调用者,出现了什么错误
boolean invaildInput = false;
public double myPow(double x, int n) {
invaildInput= false;
// 1. 对底数为0,且指数是负数的情况,进行特殊处理
// 因为0不能作为除数来处理
if (x == 0.0 && n < 0) {
invaildInput = true;
return 0.0;
}
// 2. 当指数为0时,我们取其绝对值
int abs = n;
if (n < 0) abs = -abs;
// 3. 调用PowerWithUnsigned方法,得到幂次结果
double result = PowerWithUnsigned(x,abs);
// 4. 如果指数为0,那么就取其倒数
if (n < 0) result = 1.0/result;
// 5. 最后返回结果
return result;
}
// 求正数的幂次结果
public double PowerWithUnsigned(double x, int n){
double result = 1.0;
for (int i = 0; i < n; i++){
result *= x;
}
return result;
}
}
2.2 快速幂 – O(logn)
时间复杂度O(logn),空间复杂度O(1)



class Solution {
public double myPow(double x, int n) {
// 1. 如果输入值为0,则直接返回0
if(x == 0) return 0;
// 2. 定义一个变量用来存储指数
long b = n;
// 3. 初始化结果值变量
double res = 1.0;
// 4. 如果指数小于0,取输入值的倒数,并取指数的绝对值
if(b < 0) {
x = 1 / x;
b = -b;
}
// 5. 指数大于0
while(b > 0) {
// 每当n 为奇数时,将多出的一项x 乘入 res
if((b & 1) == 1) res *= x;
x *= x;
// n/2
b >>= 1;
}
return res;
}
}
2.3 递归 – O(logn)
时间复杂度O(logn),空间复杂度O(n)
思路同2.2基本相同,只不过这里直接采用公式进行了递归.
class Solution {
public double myPow(double x, int n) {
if(n == 0)
return 1;
if(n<0){
return 1/x * myPow(1/x, -(n + 1));
}
return (n%2 == 0) ? myPow(x*x, n/2) : x*myPow(x*x, n/2);
}
}

3. 参考资料
[1] 面试题16. 数值的整数次方(快速幂,清晰图解)-- 快速幂算法图片来源


![[计算机网络(第八版)]第三章 数据链路层(学习笔记)](https://img-blog.csdnimg.cn/ba6f0d60ebe74661b339308d5b442428.png)