条件概率

定义：设A、B是两个事件，且，P(A) > 0 则称 为事件A发生的条件下事件B的条件概率

对这个式子进行变形，即可得到概率的乘法公式：

P(A) > 0 时，则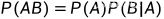

P(B) > 0 时，则

乍一看，这个式子不就是把除法形式写成了乘法形式嘛，不然不然，这个区别是本质的，分母不为0很关键，而且看法也不同：前面的是条件概率，后面的是概率的乘法公式。

概率的乘法公式，起源于概率的乘法原理，一件事情发生的概率等于造成这件事发生的接连发生的事件概率的乘积，如果要让A，B同时发生，那么就让其中一个先发生，不妨设为A吧，A发生以后B再发生，这样子的话，A，B就会同时发生了，根据概率的乘法原理如下

概率的乘法公式的n个事件的形式:

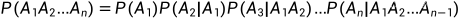
如果要使n件事件同时发生，不妨先发生 ，接着再发生 ,

全概率公式

若事件满足下列两条

1. 

2. 

则称 为完备事件组

全概率公式如:

以n=3为例：

比如一件事情的结果就只有三种 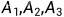，也知道它们发生的概率，但是呢，这时候偏偏有一个事件B也发生了，我们的目的是找出B发生的概率，于是呢，我们让B与 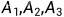发生联系，从而进行试验，可以得到各自的条件概率 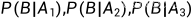,那么这就足够了，我们就可以得到事件B发生的概率

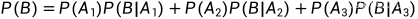
贝叶斯公式

贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设：“如果一个袋子中共有 10 个球，分别是黑球和白球，但是我们不知道它们之间的比例是怎么样的，现在，仅通过摸出的球的颜色，是否能判断出袋子里面黑白球的比例？”

简单而言就是已知结果找原因

设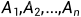是完备事件组，且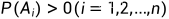

B 为任意事件，P(B) > 0,则

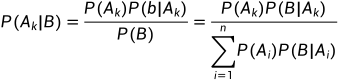
对于这个公式的理解主要靠上面那句话。什么是结果?什么又是原因？对于全概率公式，我们说是为了求事件B发生的概率所做的试验，这些就是结果了，那么反过来，我们找原因，这些完备事件在B发生时的条件概率就是我们所要查照的原因了。

通常把 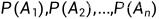叫做先验概率，就是做试验前的概率，就是经验了；而把 叫做后验概率，在统计决策中十分重要，由此得到的决策叫做贝叶斯决策。也就是说我们在对经验不断地更新和修正，当然是利用生活实践，即所谓试验。（又是一个人生哲理，对于很多事情，就是要不断地利用当前的经验来进行试错，不断地修正，从而达到自我的一个最佳状态

马尔科夫链

定义一种表述方法，考虑只取有限个或可数个值的随机过程 若 ，则称过程在 n 时刻处于状态 i。

马尔可夫性：给定过去的状态 和现在的状态 ，将来的状态 的条件分布与过去的状态独立，只依赖于现在的状态，这样的性质称为马尔可夫性。

如果我们用 A表示过去的状态，用 B 表示现在的状态，而用 C 表示将来的状态，即

则马尔科夫性可以用条件概率直观表示为

等价推出

因此马尔可夫性也可以理解为在已知现在状态的条件下，过去与将来相互独立

马尔科夫链：设随机过程 的状态空间 I 有限或可列，如果它具有马尔科夫性，即对任意的状态 和任意的 有

则称随机过程 是马尔科夫链，简称马氏链

把具有马尔可夫性的随机过程称为马尔可夫过程。

马尔可夫链是离散时间离散状态的马尔可夫过程。

泊松过程是连续时间离散状态的马尔可夫过程。

布朗运动是连续时间连续状态的马尔科夫过程。

转移概率和转移矩阵

考虑马尔科夫链 及其状态空间 ,将条件概率定义为

用来表示过程在 m 时刻处于状态 i 的条件下，经过 n 步后转移到状态 j 的转移概率。 由于概率是非负的，且过程在 m 时刻从任何一个状态 i 出发，到 m + n 时刻必须转移到 I 中的某个状态，所以有

时齐的马尔可夫链：如果 不依赖于 n，则过程 是时齐的马尔可夫链。定义马尔可夫链的一步转移概率为

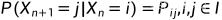
一步转移概率 的含义是处在状态 i 的过程下一次转移到状态 j的概率，显然一步转移概率也具有如下性质：

不妨设状态空间为自然数集 ,定义一步转移概率矩阵为

显然一步转移概率矩阵 P 的所有元素都是非负的，且每一行的元素之和为 1 。

在马尔可夫链是时齐的情形下，条件概率 只与 i , j 以及时间间隔 n 有关，定义马尔可夫链的 n 步转移概率为

其含义是处在状态 i 过程将在 n 次转移之后处于状态 j 的概率。类似的可以定义 n 步转移概率矩阵为

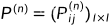
如果想判断一个马尔可夫链是时齐的，只需要证明它的一步转移概率与时间 n 无关即可