电子技术——B类输出阶
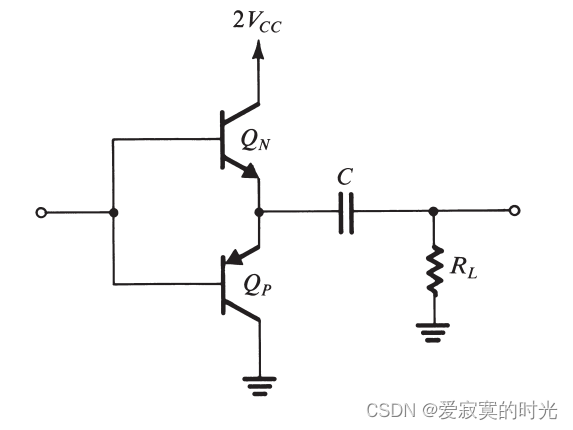
下图展示了一个B类输出阶的原理图,B类输出阶由两个互补的BJT组成,不同时导通。
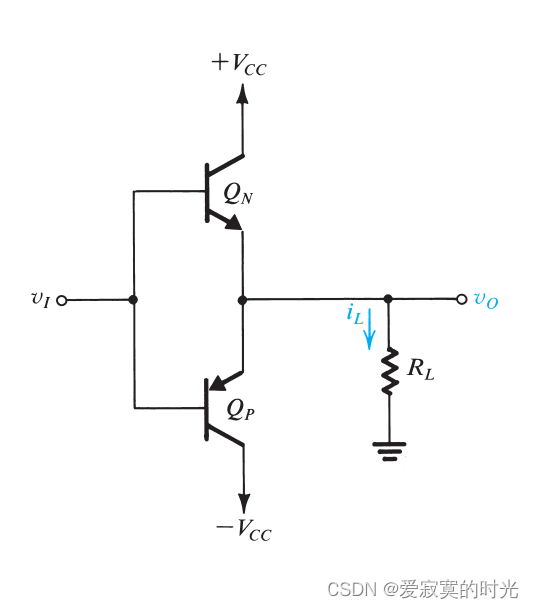
原理
当输入电压 v I = 0 v_I = 0 vI=0 的时候,两个晶体管都截止输出电压为零。当 v I v_I vI 上升至超过+0.5V的时候,此时 Q N Q_N QN 导通,此时 Q N Q_N QN 作为射极跟随器。 v O = v I − v B E N v_O = v_I - v_{BEN} vO=vI−vBEN 跟随电压 v I v_I vI ,由 Q N Q_N QN 提供负载电流。同时 Q P Q_P QP 处于反向截止状态。
当 v I v_I vI 下升至超过-0.5V的时候,此时 Q P Q_P QP 导通,此时 Q P Q_P QP 作为射极跟随器。 v O = v I + v E B P v_O = v_I + v_{EBP} vO=vI+vEBP 跟随电压 v I v_I vI ,由 Q P Q_P QP 提供负载电流。同时 Q N Q_N QN 处于反向截止状态。
B类输出阶的偏置电流为零,并且晶体管只在信号输入的时候导通,该电路也称为 推挽电路 : Q N Q_N QN 负责正向时向 R L R_L RL 推电流,而 Q P Q_P QP 负责负向的时候拉电流。
传导特性
下图是B类输出阶的传递曲线:
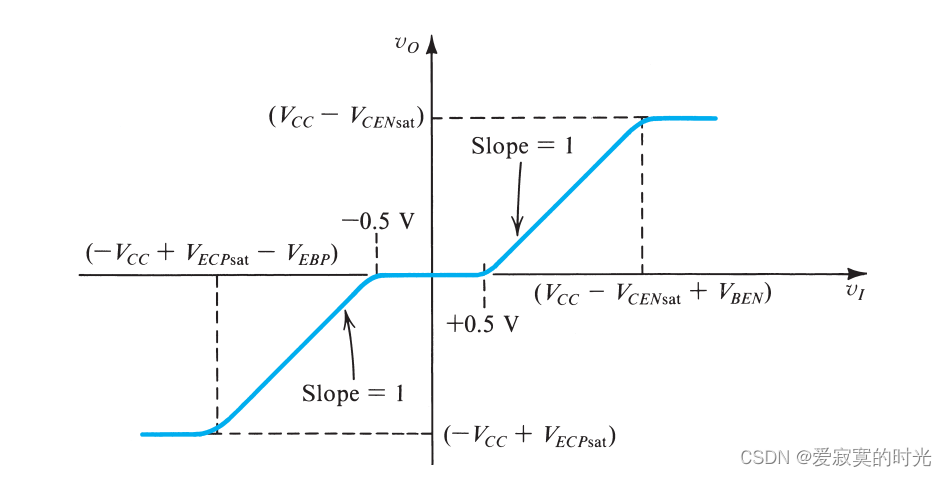
图中在零点的附近存在一段两个晶体管同时截止的区域,此时输出电压为零。我们称这段区域为 死区 ,这个现象称为 交越失真 ,其输出波形如下:
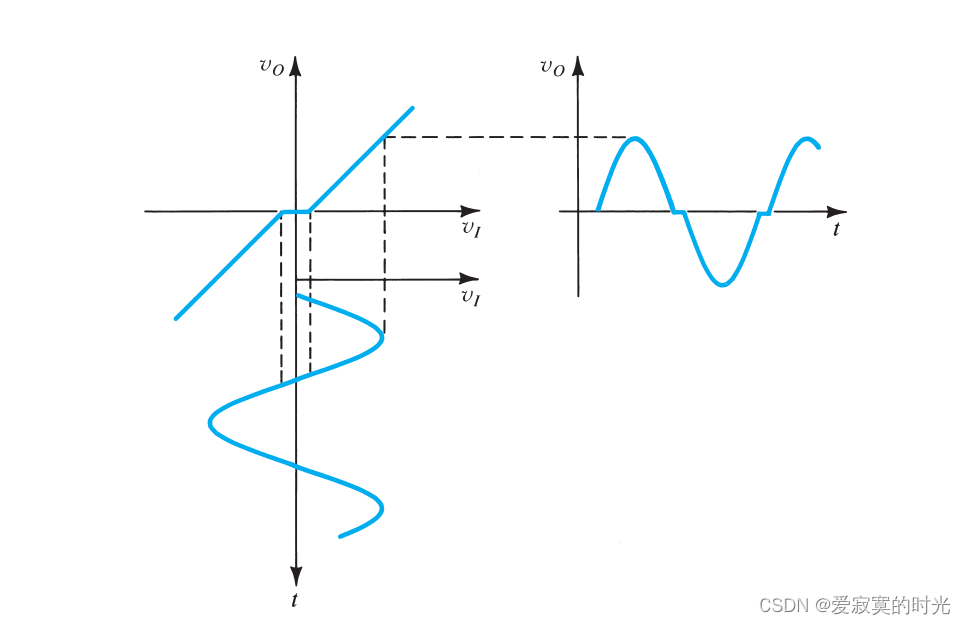
尤其是小信号输出的时候,交越失真的现象就会特别明显,对于音频系统会产生杂音。
能量转换效率
为了计算能量转换效率,我们忽略交越失真,并且输出是一个峰值为 V o ^ \hat{V_o} Vo^ 的正弦信号,则负载的平均功率为:
P L = 1 2 V o ^ 2 R L P_L = \frac{1}{2}\frac{\hat{V_o}^2}{R_L} PL=21RLVo^2
两个电压源的输出电流都是峰值为 V o ^ / π R L \hat{V_o} / \pi R_L Vo^/πRL 的半波,因此两个电压源的输出功率为:
P S + = P S − = 1 π V o ^ R L V C C P_{S+} = P_{S-} = \frac{1}{\pi} \frac{\hat{V_o}}{R_L} V_{CC} PS+=PS−=π1RLVo^VCC
总电压源功率为:
P S = 2 π V o ^ R L V C C P_S = \frac{2}{\pi} \frac{\hat{V_o}}{R_L} V_{CC} PS=π2RLVo^VCC
则能量转换效率为:
η = ( 1 2 V o ^ 2 R L ) / ( 2 π V o ^ R L V C C ) = π 4 V o ^ V C C \eta = (\frac{1}{2} \frac{\hat{V_o}^2}{R_L}) / (\frac{2}{\pi}\frac{\hat{V_o}}{R_L}V_{CC}) = \frac{\pi}{4} \frac{\hat{V_o}}{V_{CC}} η=(21RLVo^2)/(π2RLVo^VCC)=4πVCCVo^
当 V o ^ ≃ V C C \hat{V_o} \simeq V_{CC} Vo^≃VCC 的时候功率达到最大值为:
η m a x = π 4 = 78.5 % \eta_{max} = \frac{\pi}{4} = 78.5\% ηmax=4π=78.5%
这个值远高于A类输出阶的最大能量转换效率,并且此时负载达到最大功率:
P L m a x = 1 2 V C C 2 R L P_{Lmax} = \frac{1}{2}\frac{V_{CC}^2}{R_L} PLmax=21RLVCC2
耗散功率
不像A类输出阶在静态点处耗散功率最大,B类输出阶在静态点处耗散功率为零,当输入信号的时候,平均耗散功率为:
P D = P S − P L = 2 π V o ^ R L V C C − 1 2 V o ^ 2 R L P_D = P_S - P_L = \frac{2}{\pi} \frac{\hat{V_o}}{R_L} V_{CC} - \frac{1}{2}\frac{\hat{V_o}^2}{R_L} PD=PS−PL=π2RLVo^VCC−21RLVo^2
由于电路的对称性我们知道, Q N Q_N QN 和 Q P Q_P QP 均使用一半的耗散功率 1 2 P D \frac{1}{2}P_D 21PD 。因为 P D P_D PD 依赖于 V o ^ \hat{V_o} Vo^ ,我们可以求得 P D P_D PD 的最大值,上式是一个二次函数,在:
V o ^ ∣ P D m a x = 2 π V C C \hat{V_o} |_{P_{Dmax}} = \frac{2}{\pi} V_{CC} Vo^∣PDmax=π2VCC
处达到最大值为:
P D m a x = 2 V C C 2 π 2 R L P_{Dmax} = \frac{2V_{CC}^2}{\pi^2R_L} PDmax=π2RL2VCC2
能量转换效率为:
η = 50 % \eta = 50\% η=50%
下图描述了B类输出阶的耗散功率曲线:

这样的曲线通常在IC类放大器的datasheet中给出。我们发现当输出电压超过
2
π
V
C
C
\frac{2}{\pi} V_{CC}
π2VCC 的时候,随着输出电压的增大,耗散功率减小。但是带来的代价是增大了非线性失真,由于跟随器的单位增益,这个非线性失真无法用负反馈消除,因此对于THD较小的设备通常选择较小的输出电压。
减小交越失真
交越失真可以使用高增益的运算放大器加上负反馈减小,如图:
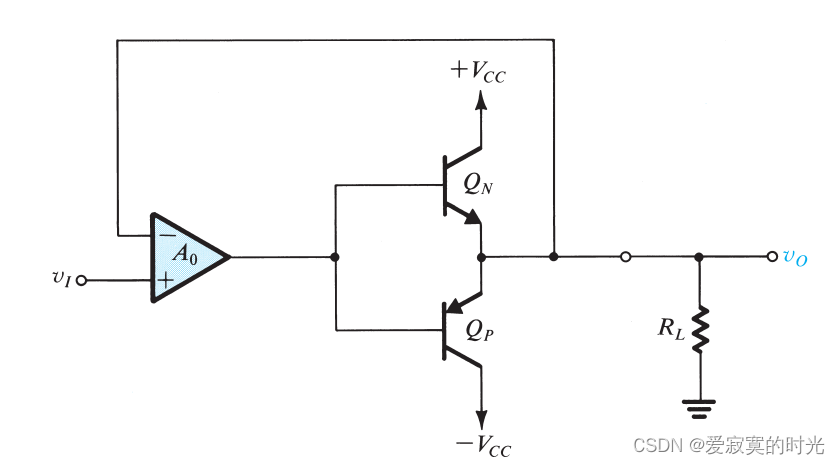
此时
±
0.7
V
\pm 0.7V
±0.7V 的死区被缩短到
±
0.7
V
/
A
0
\pm 0.7V / A_0
±0.7V/A0 这个
A
0
A_0
A0 是运放的开环增益。尽管如此,运算放大器存在大信号爬升率的影响,尤其是在高频信号下,会引入额外的信号失真。一个完美的解决方案是使用AB类输出阶。
单电源方案
B类输出阶也可以使用单电源方案,使用电容进行耦合: