Problem - F - Codeforces

思维构造题

题意:

一个长为n的直线洞窟中, 每一个1~n的整数位置都有一个洞口可以容纳一只兔子

有一只兔子在这个洞窟里四处躲藏, 每一回合都必须向左或者向右移动, 不能待在原地

你每一次都可以在兔子移动之前检查任何一个洞口

要求在最坏的情况下用最少的次数抓住这只兔子, 且输出每一步检查的洞口

题解:

首先这题拿到先看样例

不考虑兔子一开始就在2洞口的情况, 因为兔子必须要移动, 所以兔子在第一步结束时候会来到洞口2, 显然没有去搜1和3的必要, 即起点和终点不需要搜索, 因为兔子在末端洞口时, 一定会被逼到末端+1或者末端-1的位置

接下来继续模拟, 假设n=5

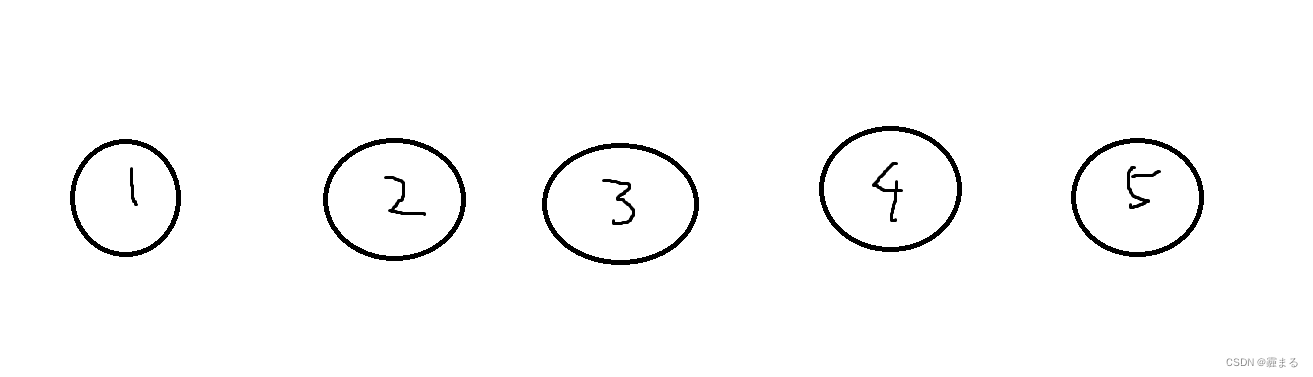
根据上文我们从2开始向右搜索, 如果兔子在4位置, 我们搜索2位置, 兔子只能向右走来到5, 因为向左走来到3位置就会被我们搜到, 接下来我们搜3, 兔子来到4, 再向右搜一个位置正好被搜到

假设兔子在3位置, 我们先搜索了2, 兔子在3位置可以跑到我们搜过的2位置去, 就正好错过了, 此时继续向右搜索来到3位置, 兔子可以走到1位置或者3位置, 和我们的位置奇偶性相同了

根据上文的模拟, 我们可以粗略得出一个结论: 当兔子和我们搜索的位置奇偶性相同时, 兔子一定会被逼到末端-1的位置被捉住, 而不同时, 兔子可以在末端的位置正好与我们错过(兔子这里考虑的是最坏情况), 但改变了奇偶性, 当我们回头再来的时候, 将被我们捉住

根据这个结论再验证几个数据之后证实是正确的之后敲代码

交了之后就会发现wa在了一个神奇的样例: n=1和n=2

特判此处得解

void solve()
{
    cin>>n;
    if(n==1)
    {
        cout<<"1\n1"<<endl;;
        return;
    }
    if(n==2) n=3;
    cout<<(n-2)*2<<endl;
    for(int i=2;i<=n-1;i++) cout<<i<<' ';
    for(int i=n-1;i>=2;i--) cout<<i<<' ';
    return;
}