1. 什么是汉诺塔

源于印度古老传说的益智玩具

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

2. 有关汉诺塔的有趣故事

想象你来到某个热带丛林，意外发现了十层之高的汉诺塔。正当你苦苦思索如何搬动它时，林中出来一个土著，毛遂自荐要帮你搬塔。他名叫二傻，戴着一个草帽，草帽上有一个2字，号称会把一到二号盘搬到任意柱。你灵机一动，问道：“你该不会有个兄弟叫三傻吧？”“对对，老爷你咋知道的？他会搬一到三号盘。“”那你去把他叫来，我不需要你了。“于是三傻来了，他也带着个草帽，上面有个3字。你说：”三傻，你帮我把头三个盘子移到c柱吧。“三傻沉吟了一会，走进树林，你听见他大叫：”二傻，出来帮我把头两个盘子搬到C!“由于天气炎热你开始打瞌睡。朦胧中你没看见二傻是怎么工作的，二傻干完以后，走入林中大叫一声：“老三，我干完了!”三傻出来，把三号盘从A搬到B，然后又去叫二傻：“老二，帮我把头两个盘子搬回A!”余下的我就不多说了，总之三傻其实只搬三号盘，其他叫二傻出来干。最后一步是三傻把三号盘搬到C，然后呼叫二傻来把头两个盘子搬回C事情完了之后你把三傻叫来，对他说：“其实你不知道怎么具体一步一步把三个盘子搬到C，是吧？”三傻不解地说：“我不是把任务干完了？”你说：“可你其实叫你兄弟二傻干了大部分工作呀？”三傻说：“我外包给他和你屁相干？”你问到：“二傻是不是也外包给了谁？“三傻笑了：“这跟我有屁相干？”你苦苦思索了一夜，第二天，你走入林中大叫：“十傻，你在哪？”一个头上带着10号草帽的人，十傻，应声而出：“老爷，你有什么事？”“我要你帮把1到10号盘子搬到C柱““好的，老爷。“十傻转身就向林内走。“慢着，你该不是回去叫你兄弟九傻吧““老爷你怎么知道的？““所以你使唤他把头九个盘子搬过来搬过去，你只要搬几次十号盘就好了，对吗？““对呀！““你知不知道他是怎么干的？““这和我有屁相干？“你叹了一口气，决定放弃。十傻开始干活。树林里充满了此起彼伏的叫声：“九傻，来一下！“ “老八，到你了！““五傻！。。。“”三傻！。。。“”大傻！“你注意到大傻从不叫人，但是大傻的工作也最简单，他只是把一号盘搬来搬去。若干年后，工作结束了。十傻来到你面前。你问十傻：“是谁教给你们这么干活的？“十傻说：“我爸爸。他给我留了这张纸条。”他从口袋里掏出一张小纸条，上面写着：“照你帽子的号码搬盘子到目标柱。如果有盘子压住你，叫你上面一位哥哥把他搬走。如果有盘子占住你要去的柱子，叫你哥哥把它搬到不碍事的地方。等你的盘子搬到了目标，叫你哥哥把该压在你上面的盘子搬回到你上头。“你不解地问：“那大傻没有哥哥怎么办？“十傻笑了：“他只管一号盘，所以永远不会碰到那两个‘如果’，也没有盘子该压在一号上啊。”但这时他忽然变了颜色，好像泄漏了巨大的机密。他惊慌地看了你一眼，飞快地逃入树林。第二天，你到树林里去搜寻这十兄弟。他们已经不知去向。你找到了一个小屋，只容一个人居住，但是屋里有十顶草帽，写着一到十号的号码。

作者：Fireman A
链接：https://www.zhihu.com/question/24385418/answer/257751077
来源：知乎

3. 利用动画来演示汉诺塔

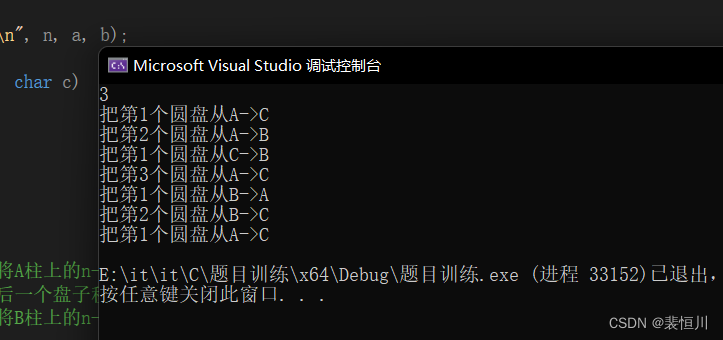
现有三个柱子A、B、C，其中有n个圆盘在A柱上，最终要实现把这n个圆盘从A柱借助B柱移动到C柱上。实现实现思路：先将n-1个圆盘从A柱移动到B柱上，然后将A柱上最后一个圆盘移动到C柱上，最后再把B柱上的n-1个圆盘移动到C柱上。

三个盘子的汉诺塔

多个盘子的汉诺塔（创意）

4. 如何用C语言实现汉诺塔

#include<stdio.h>

void move(char a,char b,int n)
{
	printf("把第%d个圆盘从%c->%c\n", n, a, b);
}
void H_tow(int n, char a, char b, char c)
{
	if (n == 1)
	{
		move(a, c, n);
	}
	else
	{
		H_tow(n - 1, a, c, b);//将A柱上的n-1个盘子借助C柱移向B柱
		move(a, c,n);//将A柱上最后一个盘子移向C柱
		H_tow(n - 1, b, a, c);//将B柱上的n-1个盘子借助A柱移向C柱
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	H_tow(n, 'A', 'B', 'C');
	return 0;
}

如果这份博客对大家有帮助，希望各位给恒川一个免费的点赞作为鼓励，并评论收藏一下，谢谢大家！！！
制作不易，如果大家有什么疑问或给恒川的意见，欢迎评论区留言。