一、概率论基础

1. 三元体定义

2. 随机变量及其分布

分布函数定义及性质：

1. 离散随机变量

• 定义：
  
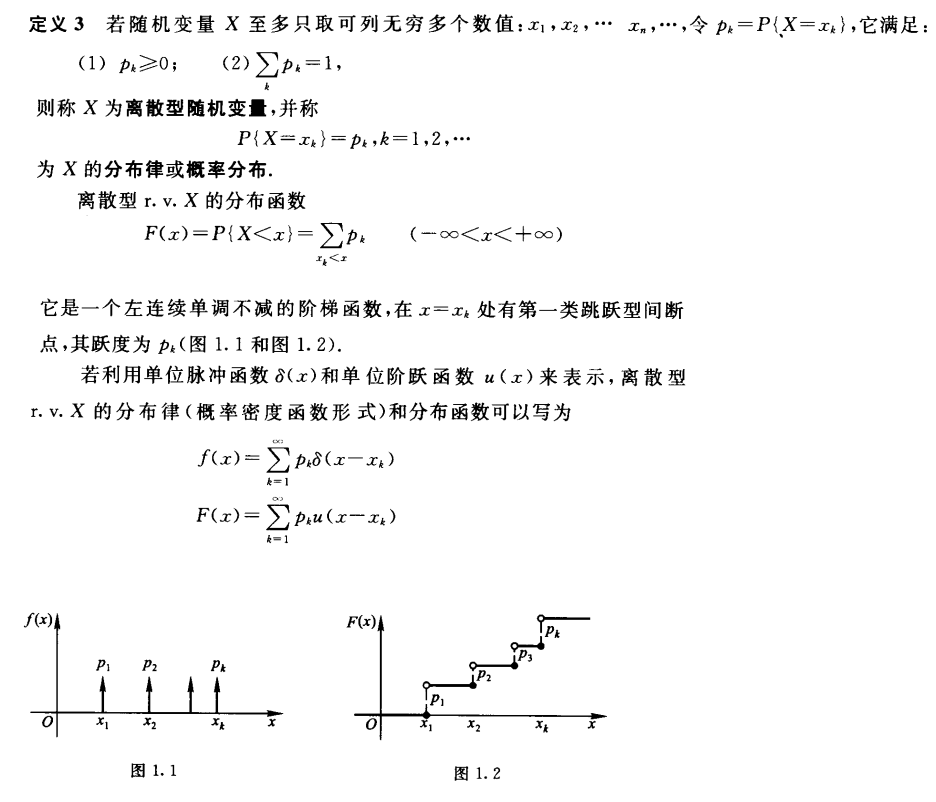
• 例题：
  

2. 连续型随机变量

• 定义：
  
• 例题：
  

3. 常见的随机变量和分布

1. 离散类

泊松分布很重要

2. 连续类

最重要的：

其他要看得：

4. 二维连续随机变量

1. 二维离散

• 定义
  
• 例题：

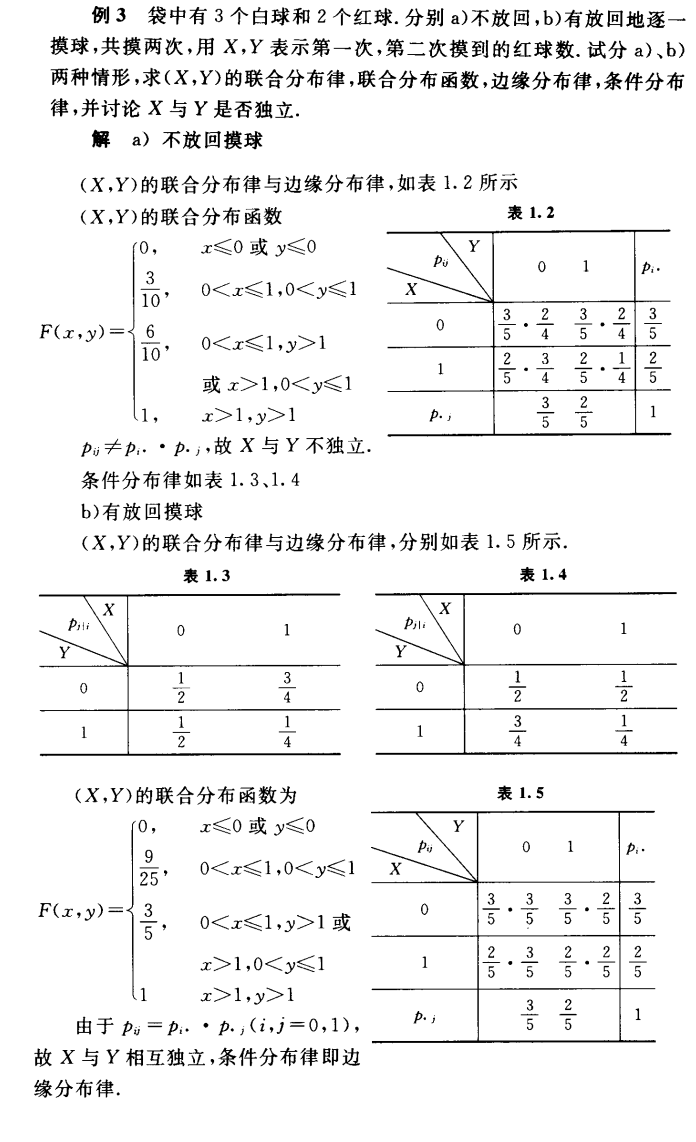
2. 二维连续

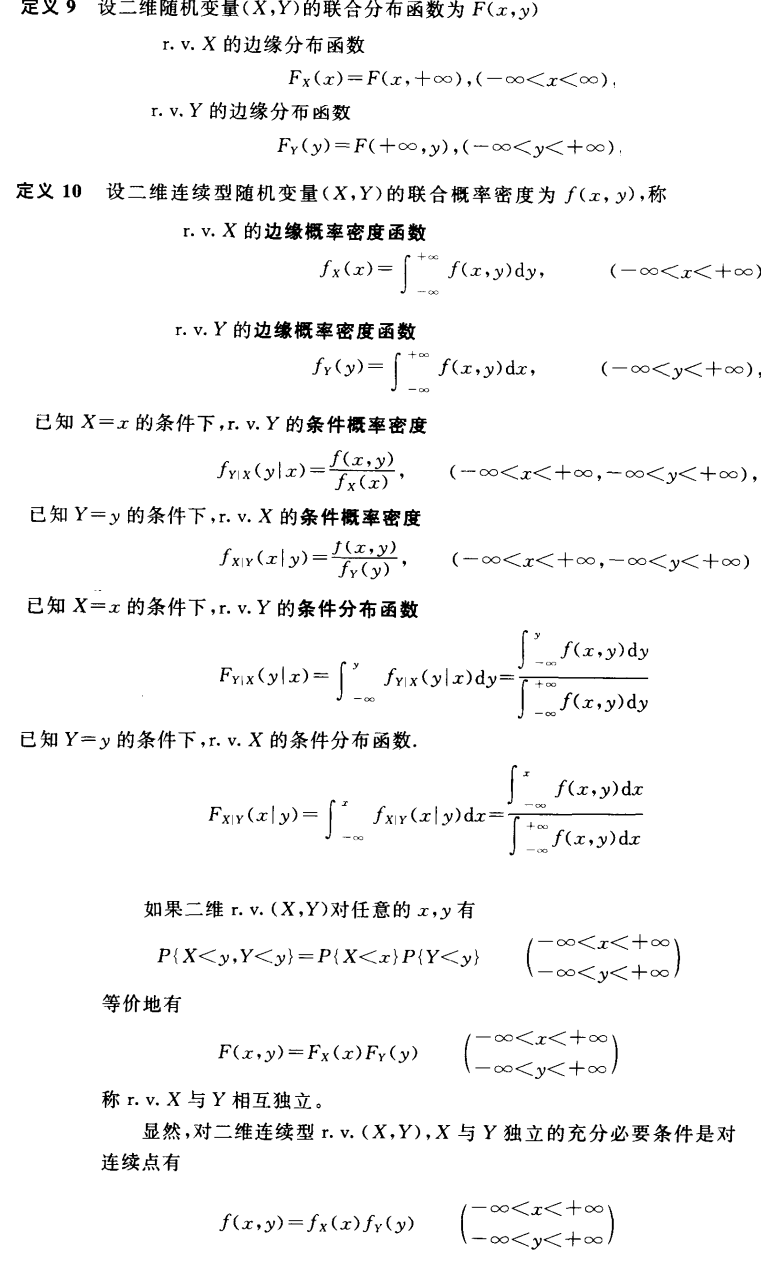
• 定义
  
  其他函数定义：

• 例题

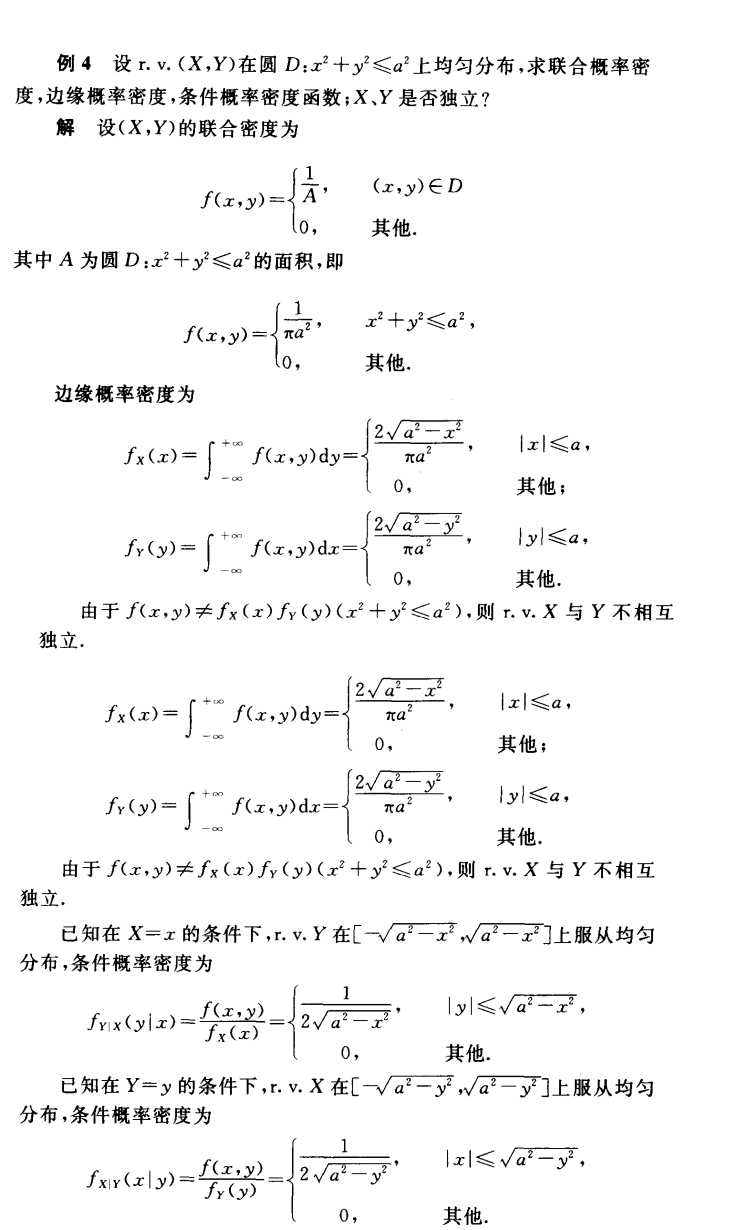
5. 随机变量函数的分布

1. 离散（可浅看）

2. 一维连续 r.v 函数分布（重要）

例题：

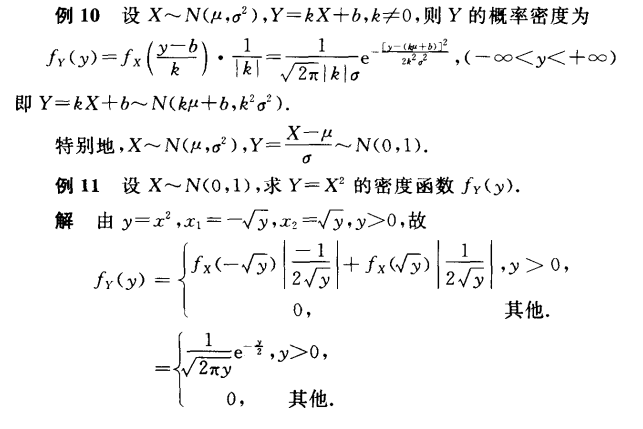
3. 二维随机变量的变换

定义

例题

没时间可以不看这个下面的

6. 随机变量的数字特征

1. 数学期望

1. 定义

2. 性质

2. 方差

1. 定义

2. 性质

3. 协方差

4. 随机变量数字特征的性质

例题

7. 特征函数

二、随机过程的基本概念

三、

四、

五、

六、