题目

T(T<=100)组样例，每次给出一棵深度为d的k叉树，

其中，第i层深的节点个数为

保证k叉树的所有节点个数tot不超过1e18，

求在k叉树上构建一棵大小恰为x的连通块，所需要断开的最少的树边的条数(x<=tot<=1e18)

思路来源

乱搞AC

题解

其实不太知道为什么算个G题，可能是因为F题卡住了太多人

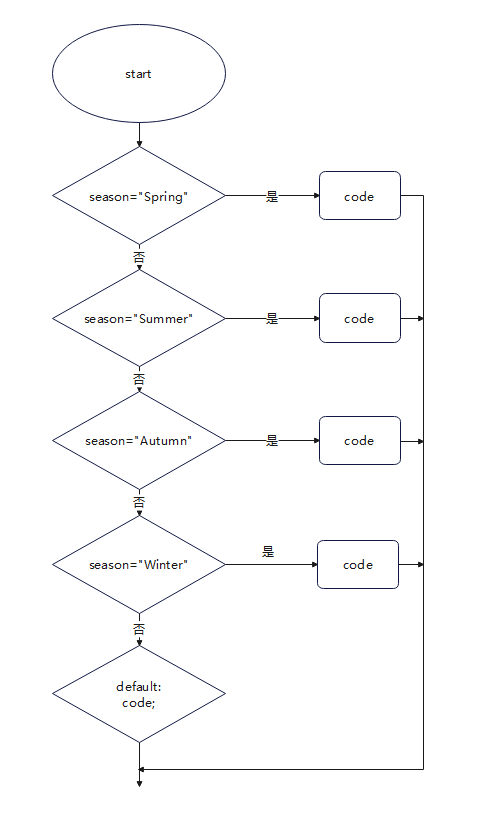
考虑连通块的点的lca位于哪一层，枚举lca所在层为第i层，

如果是第0层，不用切断，如果是第1层到第d层，需要先切断一条边，

只考虑第i层为根的这棵子树，若这棵子树不足x个点，可以直接跳过

否则，当前这棵子树总的点数一定大于x（等于x的情况直接break即可）

计当前还需要删的点的个数为sum2，当前删掉的边数为cur，

子树当前层的点为根及以下层点的总数为now，子树下一层的点为根及以下层的点数为nex

此刻，一定是优先断开靠上的边，靠上的一条边能直接削掉大小为nex的一棵子树

通过下取整确定削几棵，余数在下一层里考虑，直到要删的点为0或考虑到最后一层即可

代码

#include<bits/stdc++.h>
using namespace std;
const int N=65;
typedef long long ll;
int t,c;
ll d,k,x,a[N],sum[N],now,cur;
int main(){
	cin>>t;
	while(t--){
		cin>>d>>k>>x;
		a[0]=1;
		sum[0]=1;cur=0;
		for(int i=1;i<=d;++i){
			a[i]=1ll*a[i-1]*k;
			sum[i]=sum[i-1]+a[i];
		}
		ll ans=sum[d];
		for(int i=0;i<=d;++i){
			ll sum2=sum[i]-x,now=sum[i],cur=(i<d);
			if(sum2<0)continue;
			while(sum2>0){
				ll nex=(now-1)/k;
				cur+=sum2/nex;
				//printf("sum:%lld nex:%lld cur:%lld\n",sum,nex,cur);
				sum2%=nex;
				now=nex;
			}
			ans=min(ans,cur);
		}
		cout<<ans<<endl;
	}
	return 0;
}