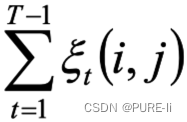多变量线性回归模型
模型参数为n+1维向量,此时模型公式为
h
θ
(
x
)
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
h_{\theta}(x)=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+...+\theta_{n}x_{n}
hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn
可以简化为
h
θ
(
x
)
=
θ
T
X
h_{\theta}(x)=\theta^\mathrm{T}\mathrm{X}
hθ(x)=θTX
此时的代价函数仍是所有建模误差的平方和,即
J
(
θ
0
,
θ
1
,
.
.
.
,
θ
n
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta_{0},\theta_{1},...,\theta_{n})=\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2}
J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
此时的批量梯度算法为
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
,
.
.
.
,
θ
n
)
\theta_{j}:=\theta_{j}-\alpha\frac{\partial }{\partial \theta_{j}}J(\theta_{0},\theta_{1},...,\theta_{n})
θj:=θj−α∂θj∂J(θ0,θ1,...,θn)
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x j ( i ) f o r j = 0 , 1 , . . . n \theta_{j}:=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_{j}^{(i)}}\quad for\quad j=0,1,...n θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i)forj=0,1,...n
特征缩放
在多维特征问题中,特征尺度越相近,梯度下降算法收敛越快。 尽量将特征尺度
x
n
x_n
xn缩放到-1~1之间。
μ
n
\mu_n
μn是平均值,
s
n
s_n
sn是方差。
x
n
=
x
n
−
μ
n
s
n
x_n=\frac{x_n-\mu_n}{s_n}
xn=snxn−μn
学习率
我们不能提前预知梯度下降算法收敛所需的迭代次数,但可以通过绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4mSi7pO3-1677383749764)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230222205742828.png)]](https://img-blog.csdnimg.cn/549215d3048f44bbae411f0e908863f3.png)
常用的学习率为0.01,0.03,0.1,0.3,1,3,10
多项式回归
线性回归不适用所有的模型,有时候可能需要二次方、三次方等模型,比如
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
2
+
θ
3
x
3
3
h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x^2_2+\theta_3x^3_3
hθ(x)=θ0+θ1x1+θ2x22+θ3x33
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2\sqrt x_2 hθ(x)=θ0+θ1x1+θ2x2
正规方程
通过正规方程解出向量,其中
X
X
X为特征矩阵
θ
=
(
X
T
X
)
−
1
X
T
y
\theta=(X^{\mathrm T}X)^{-1}X^{\mathrm T}y
θ=(XTX)−1XTy
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4pzQdqn3-1677383749764)(C:\Users\20491\AppData\Roaming\Typora\typora-user-images\image-20230223112740746.png)]](https://img-blog.csdnimg.cn/3dc2c5e2543344d8b1da5f576b12d391.png)