目录
前言
一、什么是插入排序
二、实现插入排序
三、插入排序优化
四、插入排序的特性
前言
上一篇中我们说到了《排序基础之选择排序》,这一篇我们来学习一下排序算法中的另一种基础排序算法——插入排序。
一、什么是插入排序
简单来说就是:每次只处理一个元素,把这个元素插入到前面已经排好序的元素中,即:arr[0,i)已排好序,arr[i...n)未排序,把arr[i]放到合适的位置,比如:
![]()

实现思想:双层循环,外层循环i从下标0开始遍历,内层循环j从下标i处开始遍历,将下标j和下标j-1处的两个元素进行比较,如果下标j位置处的元素比下标j-1位置处的元素小,则将二者交换位置,然后下标j继续减1向左比较它的前一个元素,直到下标j所在位置元素不大于下标j-1处的元素,则跳出该层循环,依次类推,直至排序完成。
二、实现插入排序
下面我们通过代码来实现这个排序的过程:
public class InsertSort {
public static void main(String[] args) {
Integer[] arr = {6, 4, 2, 3, 1, 5};
InsertSort.sort(arr);
for (int ele : arr) {
System.out.print(ele + " ");
}
System.out.println();
Student[] students = {new Student("张三", 89),
new Student("李四", 98),
new Student("王五", 60)};
InsertSort.sort(students);
for (Student s : students) {
System.out.println(s);
}
}
private InsertSort() {
}
public static <T extends Comparable<T>> void sort(T[] arr) {
// 将arr[i]插入到合适的位置
for (int i = 0; i < arr.length; i++) {
for (int j = i; j - 1 >= 0; j--) {
if (arr[j].compareTo(arr[j - 1]) < 0) {
swap(arr, j, j - 1);
} else {
break;
}
}
}
}
private static <T> void swap(T[] arr, int i, int j) {
T temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}运行结果如下:

三、插入排序优化
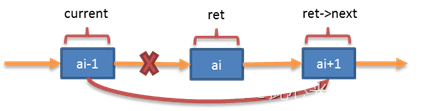
同样来看上面说到的这个数组[6,4,2,3,1,5],假如我们要对3这个元素它所在的位置进行排序,当前数组应该是:
![]()
我们上面的实现方式是用3这个元素不断的与它之前的元素进行位置的交换,要知道一次位置交换实际上进行了3次的操作,如果数据量很大的话,这个影响还是有的。现在我们想要对这种方式进行一定的优化,我们可以采用赋值的方式进行优化,思想就是:使用一个变量暂存元素3,然后进行元素比较时,如果前一个元素比3大,则直接把原来3所在位置的元素赋值为6,然后继续再比较前一个元素,直到找到对应的位置之后,将该位置的元素赋值为之前变量暂存的元素,这个流程实际上并未进行元素的交换,而是进行了元素的平移。
下面直接用代码来实现一下:
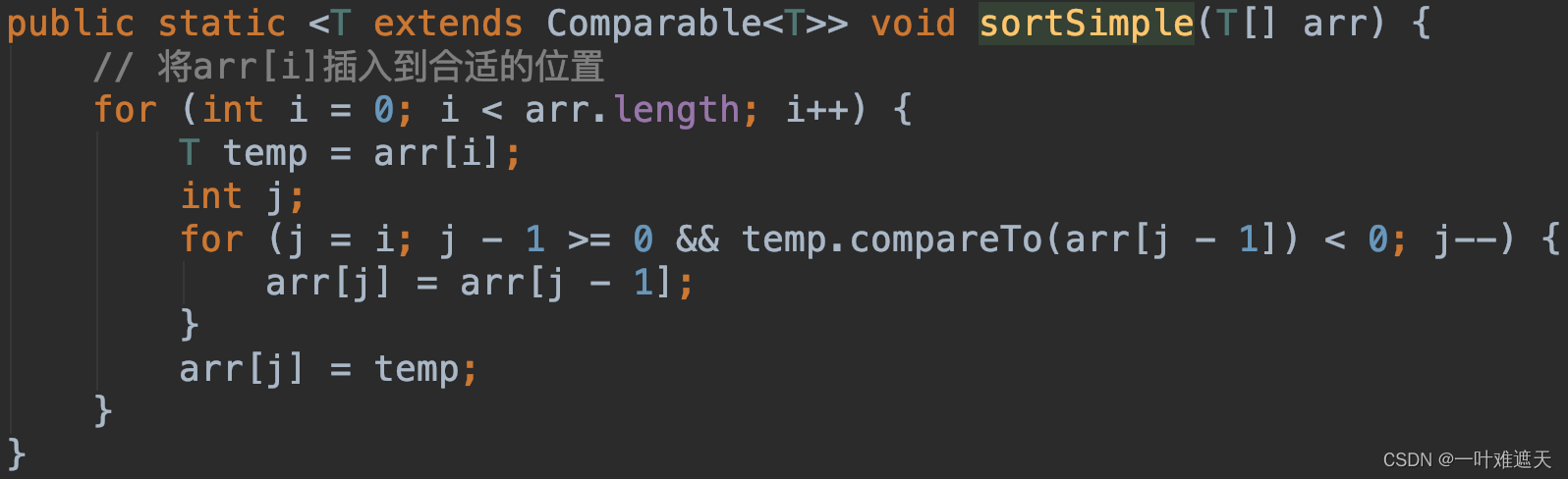
四、插入排序的特性
从上面的示例及代码中我们可以得到如下特性:
对于有序数组,插入排序的复杂度是O(n)的
但是对于整体来说,插入排序的复杂度仍然是O(n^2)的,有序数组是一种特殊情况
选择排序的复杂度永远是O(n^2)的
OK,到这里我们关于插入排序的内容就介绍的差不多了,下期再会吧!
祝:工作顺利!