目录

一.隐马尔科夫模型

二.HMM定义

三.隐马尔科夫模型的贝叶斯网络

四.HMM的确定

五.HMM的参数

六.HMM的参数总结

七.HMM的两个基本性质

1.齐次假设：

2.观测独立性假设：

八.HMM举例

九.HMM的3个基本问题

十.概率计算问题

1.直接算法

2.前向算法

3.后向算法 

十一.前向后向概率的关系

十二.单个状态的概率

十三.γ的意义

十四.两个状态的联合概率

十五.期望

十六.学习算法

---

一.隐马尔科夫模型

 概率计算
 参数估计
 模型预测

二.HMM定义

隐马尔科夫模型(HMM, Hidden Markov Model)可用标注问题，在语音识别、NLP、生物信息、模式识别等领域被实践证明是有效的算法。

HMM是关于时序的概率模型，描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，再由各个状态生成观测随机序列的过程。

隐马尔科夫模型随机生成的状态随机序列，称为状态序列；每个状态生成一个观测，由此产生的观测随机序列，称为观测序列。

        序列的每个位置可看做是一个时刻。

三.隐马尔科夫模型的贝叶斯网络

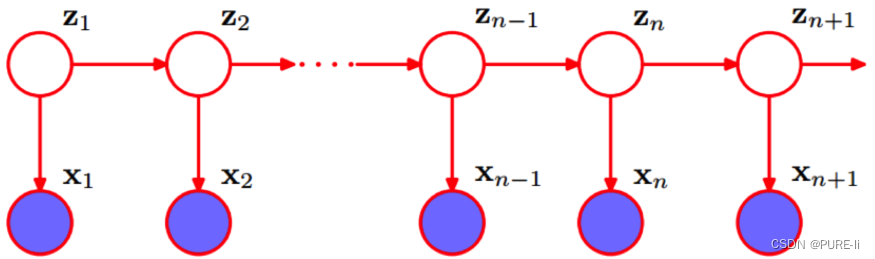
四.HMM的确定

HMM由初始概率分布π、状态转移概率分布A以及观测概率分布B确定。

五.HMM的参数

Q是所有可能的状态的集合

        N是可能的状态数 

V是所有可能的观测的集合

        M是可能的观测数

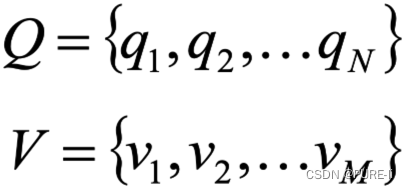
I是长度为T的状态序列，O是对应的观测序列 

A是状态转移概率矩阵

 

 

aij是在时刻t处于状态qi的条件下时刻t+1转移到状态qj的概率。

B是观测概率矩阵 

 

bik是在时刻t处于状态qi的条件下生成观测vk的概率。

π是初始状态概率向量：

 

 

πi是时刻t=1处于状态qi的概率。

六.HMM的参数总结

HMM由初始概率分布π(向量)、状态转移概率分布A(矩阵)以及观测概率分布B(矩阵)确定。π和A决定状态序列，B决定观测序列。因此，HMM可以用三元符号表示，称为
HMM的三要素：

 

七.HMM的两个基本性质

1.齐次假设：

 

2.观测独立性假设：

八.HMM举例

假设有3个盒子，编号为1、2、3，每个盒子都装有红白两种颜色的小球，数目如下：

 

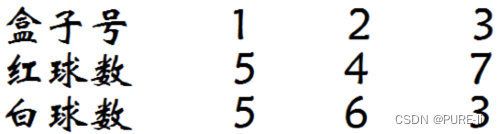
 按照下面的方法抽取小球，得到球颜色的观测序列： 按照π=(0.2,0.4,0.4)的概率选择1个盒子，从盒子随机抽出1个球，记录颜色后放回盒子；
 按照某条件概率(下页)选择新的盒子，重复上述过程；
 最终得到观测序列：“红红白白红”。 

该示例的各个参数

 状态集合：Q={盒子1，盒子2，盒子3}  观测集合：V={红，白}
 状态序列和观测序列的长度T=5
 初始概率分布π：
 状态转移概率分布A：
 观测概率分布B：

九.HMM的3个基本问题

 概率计算问题：前向-后向算法——动态规划
         给定模型和观测序列 ，计算模型λ下观测序列O出现的概率P(O| λ) 

 学习问题：Baum-Welch算法(状态未知)——EM
         已知观测序列 ，估计模型的参数，使得在该模型下观测序列P(O| λ)最大

 预测问题：Viterbi算法——动态规划
         解码问题：已知模型和观测序列求给定观测序列条件概率P(I|O, λ)最大的状态序列I 

十.概率计算问题

1.直接算法

按照概率公式，列举所有可能的长度为T的状态序列 ，求各个状态序列I 与观测序列 的联合概率
P(O,I|λ)，然后对所有可能的状态序列求和，从而得到P(O|λ)

状态序列的概率是：

对固定的状态序列I，观测序列O的概率是： 

O和I同时出现的联合概率是：

 

对所有可能的状态序列I求和，得到观测序列O的概率P(O|λ)

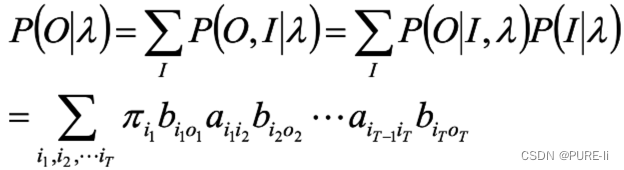
分析：加和符号中有2T个因子，I的遍历个数为NT，因此，时间复杂度为O(T NT)，复杂度过高。

2.前向算法

定义：给定λ，定义到时刻t部分观测序列为o1,o2…ot且状态为qi的概率称为前向概率，记做：

         

可以递推计算前向概率αt(t(i)及观测序列概率P(O|λ) 

        

递推：对于t=1,2…T-1

         

最终： 

         

3.后向算法 

定义：给定λ，定义到时刻t状态为qi的前提下，从t+1到T的部分观测序列为ot+1,ot+2…oT 的概率为后向概率，记做：

 

可以递推计算后向概率βt(i)及观测序列概率P(O|λ) 

 初值：

        

 递推：对于t=T-1,T-2…,1

         

 最终：

        

为了计算在时刻t状态为qi条件下时刻t+1之后的观测序列为ot+1,ot+2…oT的后向概率βt(i)，只需要考虑在时刻t+1所有可能的N个状态qj的转移概率(aij项)，以及在此状态下的观测ot+1的观测概率(bjot+1项)，然后考虑状态qj之后的观测序列的后向概率βt+1(j)

十一.前向后向概率的关系

 

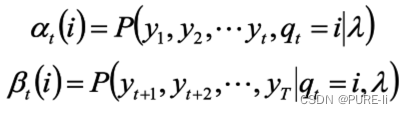
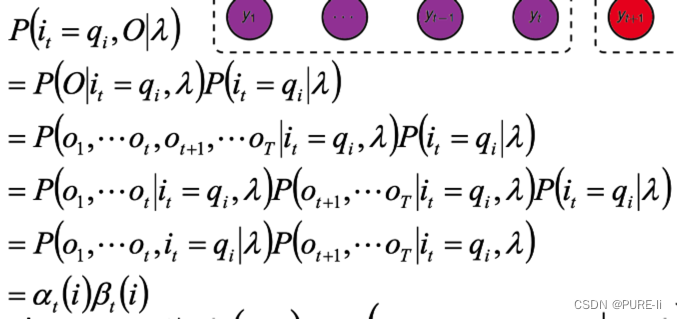
十二.单个状态的概率

求给定模型λ和观测O，在时刻t处于状态qi的概率。

根据前向后向概率的定义， 

 

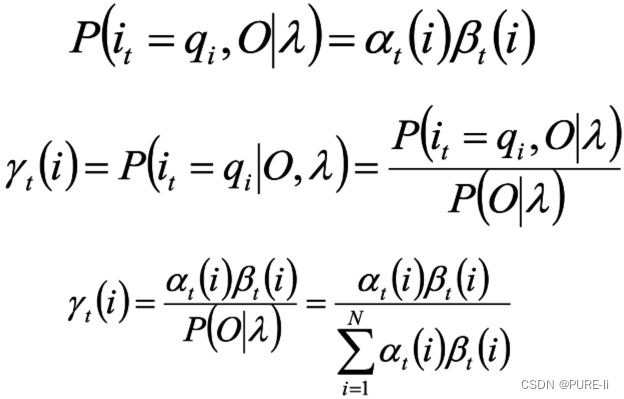
十三.γ的意义

 

给定模型和观测序列，时刻t处于状态qi的概率为：

 

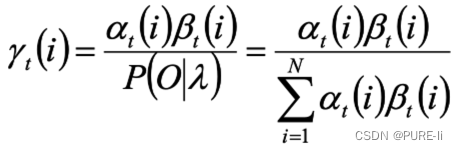
十四.两个状态的联合概率

求给定模型λ和观测O，在时刻t处于状态qi并且时刻t+1处于状态qj的概率。

 

 

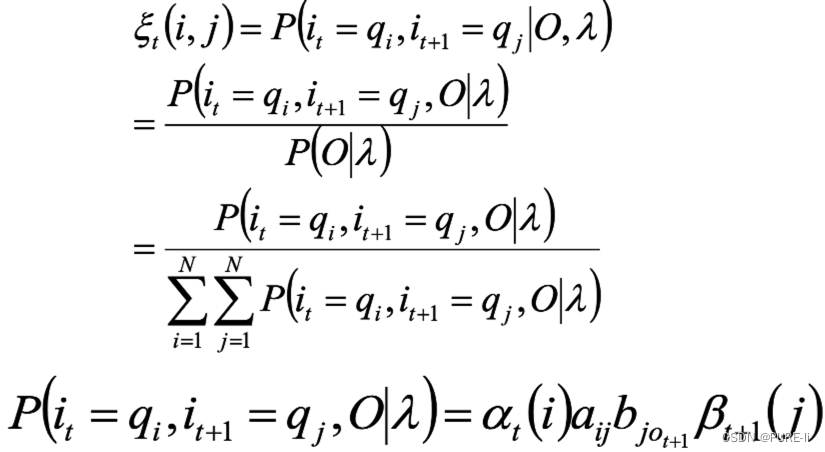
十五.期望

在观测O下状态i出现的期望：

 

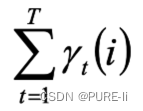
在观测O下状态i转移到状态j的期望：

 

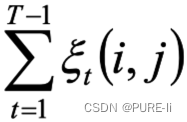
十六.学习算法

若训练数据包括观测序列和状态序列，则HMM的学习非常简单，是监督学习； 

若训练数据只有观测序列，则HMM的学习需要使用EM算法，是非监督学习。