1、删除链表的倒数第 N 个结点(链表,双指针)
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
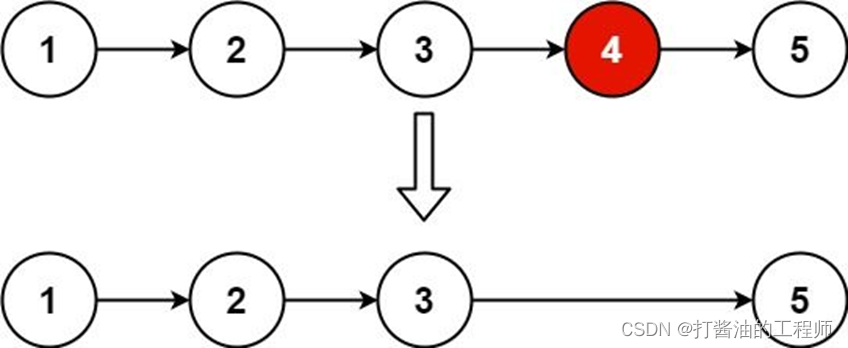
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
提示:
- 链表中结点的数目为 sz
- 1 <= sz <= 30
- 0 <= Node.val <= 100
- 1 <= n <= sz
选项代码:
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
class LinkList:
def __init__(self):
self.head=None
def initList(self, data):
self.head = ListNode(data[0])
r=self.head
p = self.head
for i in data[1:]:
node = ListNode(i)
p.next = node
p = p.next
return r
def convert_list(self,head):
ret = []
if head == None:
return
node = head
while node != None:
ret.append(node.val)
node = node.next
return ret
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
v = ListNode(0, head)
handle = v
index = []
while v is not None:
index.append(v)
v = v.next
pre = len(index)-n-1
next = len(index)-n+1
index[pre].next = index[next] if next >= 0 and next < len(
index) else None
return handle.next
# %%
l = LinkList()
list1 = [1,2,3,4,5]
head = l.initList(list1)
n = 2
s = Solution()
print(l.convert_list(s.removeNthFromEnd(head, n)))
2、下一个排列(数组,双指针)
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须 原地 (https://baike.baidu.com/item/%E5%8E%9F%E5%9C%B0%E7%AE%97%E6%B3%95)修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
示例 4:
输入:nums = [1]
输出:[1]
提示:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 100
选项代码:
class Solution(object):
def nextPermutation(self, nums):
ls = len(nums)
if ls <= 1:
return
pair = []
for i in range(ls):
for j in range(i + 1, ls):
if nums[i] < nums[j]:
pair.append([i,j])
pos = 0
if len(pair) > 0:
self.swap(nums, pair[-1][0], pair[-1][1])
pos = pair[-1][0] + 1
for i in range(pos, ls):
for j in range(i + 1, ls):
if nums[i] > nums[j]:
self.swap(nums, i, j)
return nums
def swap(self, nums, index1, index2):
if index1 == index2:
return
nums[index1], nums[index2] = nums[index2], nums[index1]
# %%
s = Solution()
print(s.nextPermutation(nums = [1,2,3]))
3、迷宫问题,需要用递归(图算法)
贡献者:adsls630ef
问题描述:一只老鼠在一个n×n迷宫的入口处,它想要吃迷宫出口处放着奶酪,问这只老鼠能否吃到奶酪?如果可以吃到,请给出一条从入口到奶酪的路径。 思考:解决问题之前,我们首先要做的就是仔细研究问题,找出问题的已知条件和要得到的是什么。和解数学问题、物理问题一样要先弄懂问题。那么,老鼠走迷宫问题的已知条件有什么呢? 数学模型重新定义问题: 问题:问老鼠能否吃到奶酪就是问能否找到一条从迷宫入口到出口的路径。如果不能找到,那么老鼠就吃不到奶酪;如果能够找到,那么就给出这条路径。 观察10×10的迷宫。这个迷宫其实是由10×10=100个格子组成的,其中绿色格子代表墙,白色格子代表路,如图(1)所示。“绿色格子代表墙,白色格子代表路”是用语言形式描述的,需要转换成数学的形式。用1和0分别定义绿色格子和白色格子,可以得到如图(2)的迷宫。 将上面10×10的迷宫定义为如下的二维数组,即 m[10][10]=[1,1,1,0,1,1,1,1,1,1, 1,0,0,0,0,0,0,0,1,1, 1,0,1,1,1,1,1,0,0,1, 1,0,1,0,0,0,0,1,0,1, 1,0,1,0,1,1,0,0,0,1, 1,0,0,1,1,0,1,0,1,1, 1,1,1,1,0,0,0,0,1,1, 1,0,0,0,0,1,1,1,0,0, 1,0,1,1,0,0,0,0,0,1, 1,1,1,1,1,1,1,1,1,1] 有了对迷宫的数学定义,就可以很简单的定义迷宫的入口和出口了。迷宫的入口是m[0][3],出口是m[7][9]。老鼠走迷宫问题就是要找一条从入口到出口的路径,如果存在就返回这条路径;如果不存在,就返回不存在这种路径。也就是说,要在二维数组m中找一条从m[0][3]到m[7][9]全部为0的路径。 请使用递归解决迷宫路径查找问题。
以下程序实现了这一功能,请你填补空白处内容:
def maze(m, n, route, pos, export):
"""走迷宫
m - 迷宫数组,列表
n - 迷宫阶数
route - 可能的路线,列表
pos - 当前位置,元组
export - 出口位置,元组
"""
route.append(pos)
if pos == export:
print(route)
if pos[0] > 0 and m[pos[0]-1][pos[1]] == 0 and (pos[0]-1,pos[1]) not in route:
maze(m, n, route[:], (pos[0]-1,pos[1]), export)
if pos[0] < n-1 and m[pos[0]+1][pos[1]] == 0 and (pos[0]+1,pos[1]) not in route:
maze(m, n, route[:], (pos[0]+1,pos[1]), export)
if pos[1] > 0 and m[pos[0]][pos[1]-1] == 0 and (pos[0],pos[1]-1) not in route:
maze(m, n, route[:], (pos[0],pos[1]-1), export)
________________________________;
m = [
[1,1,1,0,1,1,1,1,1,1],
[1,0,0,0,0,0,0,0,1,1],
[1,0,1,1,1,1,1,0,0,1],
[1,0,1,0,0,0,0,1,0,1],
[1,0,1,0,1,1,0,0,0,1],
[1,0,0,1,1,0,1,0,1,1],
[1,1,1,1,0,0,0,0,1,1],
[1,0,0,0,0,1,1,1,0,0],
[1,0,1,1,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
maze(m, len(m), list(), (0,3), (7,9))
选项代码:
if pos[1] < n - 1 and m[pos[0]][pos[1] + 1] == 0 and (pos[0], pos[1] + 1) not in route:
maze(m, n, route[:], (pos[0], pos[1] + 1), export)