文章目录
- 单一输出感知机
- 多输出感知机
- MLP反向传播
单一输出感知机
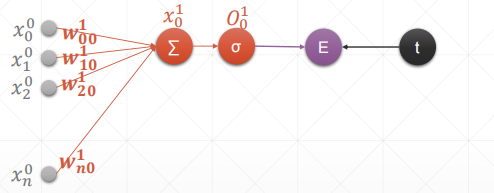
内容解释:
- w 00 1 w^1_{00} w001:输入标号1连接标号0(第一层)
- x 0 0 x_0^0 x00:第0层的标号为0的值
- O 1 1 O_1^1 O11:第一层的标号为0的输出值
- t:真实值
- σ \sigma σ:激活函数
公式推导:
E
=
1
2
(
O
0
1
−
t
)
\begin{aligned} E=\frac{1}{2}(O_0^1-t)^\ \end{aligned}
E=21(O01−t)
添加常数便于求导,不影响单调性
∂
E
∂
w
j
0
=
(
O
0
−
t
)
∂
O
0
∂
w
j
0
=
(
O
0
−
t
)
∂
σ
(
x
0
)
∂
w
j
0
=
(
O
0
−
t
)
O
0
(
1
−
O
0
)
∂
x
0
1
∂
w
j
0
注:
[
σ
(
x
0
)
=
O
0
]
=
(
O
0
−
t
)
O
0
(
1
−
O
0
)
x
j
0
\begin{aligned} \frac{\partial E}{\partial w_{j0}} &=(O_0-t)\frac{\partial O_0}{\partial w_{j0}}\\ &=(O_0-t)\frac{\partial \sigma(x_0)}{\partial w_{j0}}\\ &=(O_0-t) O_0(1- O_0)\frac{\partial x_0^1}{\partial w_{j0}} 注:[\sigma(x_0)=O_0]\\ &=(O_0-t) O_0(1- O_0)x_j^0 \end{aligned}
∂wj0∂E=(O0−t)∂wj0∂O0=(O0−t)∂wj0∂σ(x0)=(O0−t)O0(1−O0)∂wj0∂x01注:[σ(x0)=O0]=(O0−t)O0(1−O0)xj0
简单实践代码:
x = torch.randn(1,10)
w = torch.randn(1,10,requires_grad=True)
o = torch.sigmoid(x@w.t())
loss = F.mse_loss(torch.ones(1,1),o)
loss.shape
loss.backward()
w.grad

多输出感知机
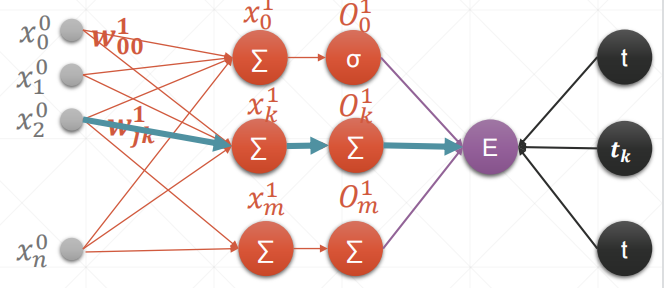
内容解释:
和单层的一摸一样,只是多了几个输出,注意下标即可
公式推导:
E
=
1
2
∑
(
O
i
k
−
t
k
)
\begin{aligned} E=\frac{1}{2}\sum(O_i^k-t_k)^\ \end{aligned}
E=21∑(Oik−tk)
添加常数便于求导,不影响单调性
∂
E
∂
w
j
k
=
(
O
k
−
t
k
)
∂
O
k
∂
w
j
k
注:
[
下标对上才有值
]
=
(
O
k
−
t
k
)
∂
σ
(
x
k
)
∂
w
j
k
=
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
∂
x
k
1
∂
w
j
k
=
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
x
j
1
\begin{aligned} \frac{\partial E}{\partial w_{jk}} &=(O_k-t_k)\frac{\partial O_k}{\partial w_{jk}}注:[下标对上才有值]\\ &=(O_k-t_k)\frac{\partial \sigma(x_k)}{\partial w_{jk}}\\ &=(O_k-t_k) O_k(1- O_k)\frac{\partial x_k^1}{\partial w_{jk}} \\ &=(O_k-t_k) O_k(1- O_k)x_j^1 \end{aligned}
∂wjk∂E=(Ok−tk)∂wjk∂Ok注:[下标对上才有值]=(Ok−tk)∂wjk∂σ(xk)=(Ok−tk)Ok(1−Ok)∂wjk∂xk1=(Ok−tk)Ok(1−Ok)xj1
即只需要输出和对应输入即可计算
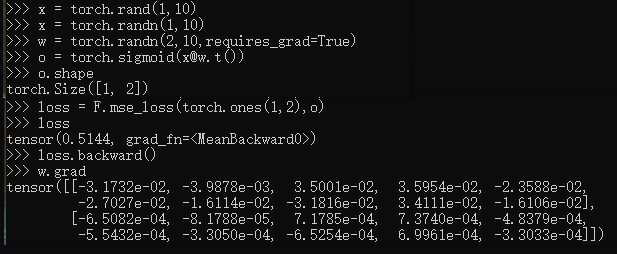
简单实践代码:
x = torch.randn(1,10)
w = torch.randn(2,10,requires_grad=True)
o = torch.sigmoid(x@w.t())
loss = F.mse_loss(torch.ones(1,2),o)
loss.shape
loss.backward()
w.grad
MLP反向传播
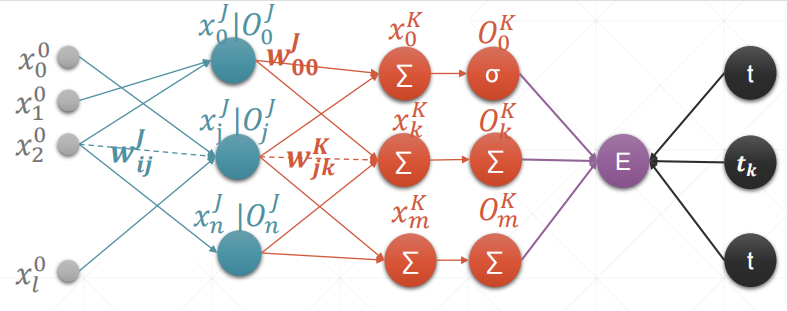
内容解释:
MLP即Multi-Layer Perceptron,多层感知机
公式推导:
∂
E
∂
W
i
j
=
∂
∂
W
i
j
1
2
∑
k
∈
K
(
O
k
−
t
k
)
2
=
∑
k
∈
K
(
O
k
−
t
k
)
∂
∂
W
i
j
O
k
=
∑
k
∈
K
(
O
k
−
t
k
)
∂
∂
W
i
j
σ
(
x
k
)
=
∑
k
∈
K
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
∂
x
k
∂
w
i
j
=
∑
k
∈
K
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
∂
x
k
∂
O
j
⋅
∂
O
j
∂
w
i
j
=
∑
k
∈
K
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
W
j
k
∂
O
j
∂
w
i
j
=
O
j
(
1
−
O
j
)
∂
x
j
∂
W
i
j
∑
k
∈
K
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
W
j
k
=
O
j
(
1
−
O
j
)
O
i
∑
k
∈
K
(
O
k
−
t
k
)
O
k
(
1
−
O
k
)
W
j
k
注:
[
层数从左到右为
i
,
j
,
k
]
\begin{aligned} \frac{\partial E}{\partial W_{ij}} &=\frac{\partial }{\partial W_{ij}}\frac{1}{2}\sum_{k\in K}(O_k-t_k)^2\\ &=\sum_{k\in K}(O_k-t_k)\frac{\partial }{\partial W_{ij}}O_k\\ &=\sum_{k\in K}(O_k-t_k)\frac{\partial }{\partial W_{ij}}\sigma(x_k)\\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)\frac{\partial x_k}{\partial w_{ij}} \\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)\frac{\partial x_k}{\partial O_j}\cdot\frac{\partial O_j}{\partial w_{ij}}\\ &=\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\frac{\partial O_j}{\partial w_{ij}}\\ &=O_j(1-O_j)\frac{\partial x_j}{\partial W_{ij}}\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\\ &=O_j(1-O_j)O_i\sum_{k\in K}(O_k-t_k) O_k(1- O_k)W_{jk}\\ &注:[层数从左到右为 i ,j,k] \end{aligned}
∂Wij∂E=∂Wij∂21k∈K∑(Ok−tk)2=k∈K∑(Ok−tk)∂Wij∂Ok=k∈K∑(Ok−tk)∂Wij∂σ(xk)=k∈K∑(Ok−tk)Ok(1−Ok)∂wij∂xk=k∈K∑(Ok−tk)Ok(1−Ok)∂Oj∂xk⋅∂wij∂Oj=k∈K∑(Ok−tk)Ok(1−Ok)Wjk∂wij∂Oj=Oj(1−Oj)∂Wij∂xjk∈K∑(Ok−tk)Ok(1−Ok)Wjk=Oj(1−Oj)Oik∈K∑(Ok−tk)Ok(1−Ok)Wjk注:[层数从左到右为i,j,k]
如果将仅与第k层相关的信息作为一个函数可以写作:
∂
E
∂
W
i
j
=
O
i
O
j
(
1
−
O
j
)
∑
k
∈
K
δ
k
W
j
k
\begin{aligned} \frac{\partial E}{\partial W_{ij}}=O_iO_j(1-O_j)\sum_{k\in K}\delta _kW_{jk} \end{aligned}
∂Wij∂E=OiOj(1−Oj)k∈K∑δkWjk
所以一个前面层的值依赖后面层的信息,需要倒着计算才行哦