请添加图片描述

开源内容：https://github.com/TommyZihao/zihao_course/tree/main/CS224W

子豪兄B 站视频：https://space.bilibili.com/1900783/channel/collectiondetail?sid=915098

斯坦福官方课程主页：https://web.stanford.edu/class/cs224w

文章目录

DeepWalk算法
- 问题的定义
- 学习隐含特征表示
- 关键技术
- 相关工作
- 代码实战
- - 获取维基百科网页引用关联数据
  - 生成随机游走节点序列的函数
  - 生成随机游走序列
  - 训练Word2Vec模型
  - 分析Word2Vec结果
  - PCA降维可视化
  - TSNE降维可视化
Node2Vec算法
- Node2Vec
- 关键技术
- 代码实战
- - 构建Node2Vec模型
  - 节点Embedding聚类可视化
  - 节点Embedding降维可视化
思考题
总结

DeepWalk算法

背景：机器学习在稀疏性数据上很难进行处理
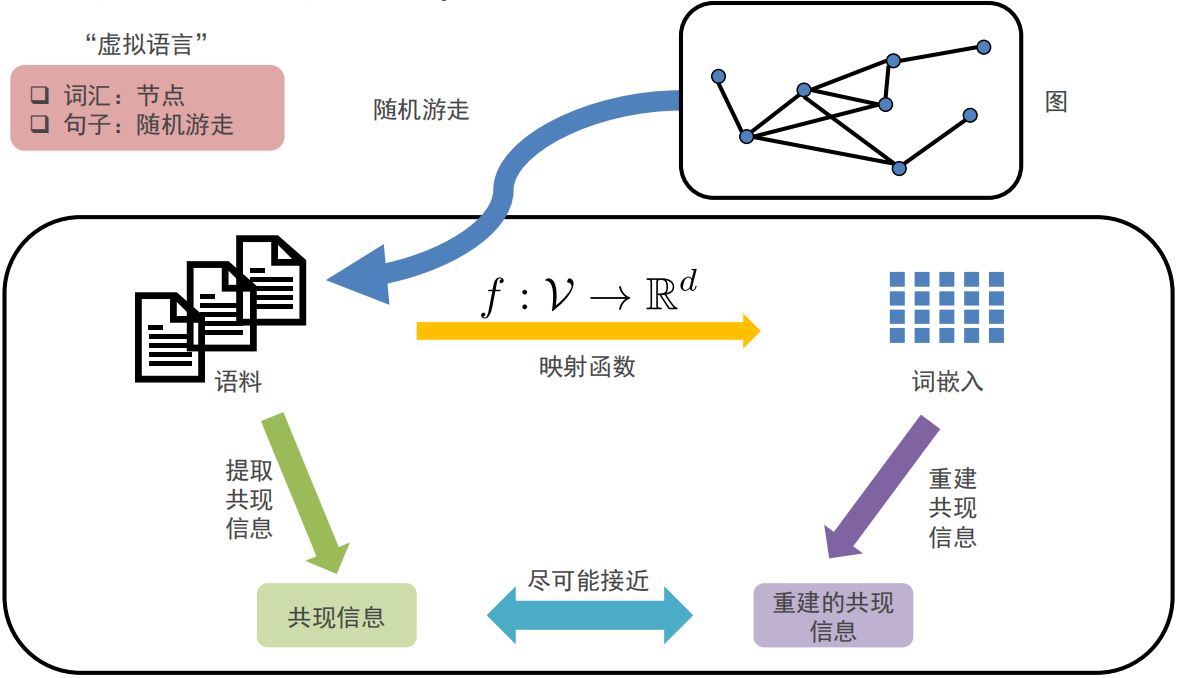
Deepwalk是用于图节点嵌入的在线机器学习算法

能够通过随机游走序列（邻居信息和社群信息）学习网络的连接结构信息，将节点编码为连续地维的稠密的向量空间
不需要重新训练，只需要输入新节点和新连接关系，再进行增量训练，可以进行并行计算

在这里插入图片描述

问题的定义

针对节点分类问题，假设图 $G = (V, E)$ 其中E $\subseteq(V×V)$ ， $G_{L}=(V,E,X,Y)$ 表示带标注的社交网络，每个节点有 $S$ 维特征， $Y$ 表示每个节点的标注
目标：通过反映连接信息的Embedding和反映节点本身的特征进行节点嵌入，得到一个 $X_{E}$ $\in$ $R^{\mid V\mid×d }$ 的嵌入，最后结合机器学习算法解决分类问题

学习隐含特征表示

DeepWalk学习到的embedding的特性
- Adaptability：灵活可变、弹性扩容
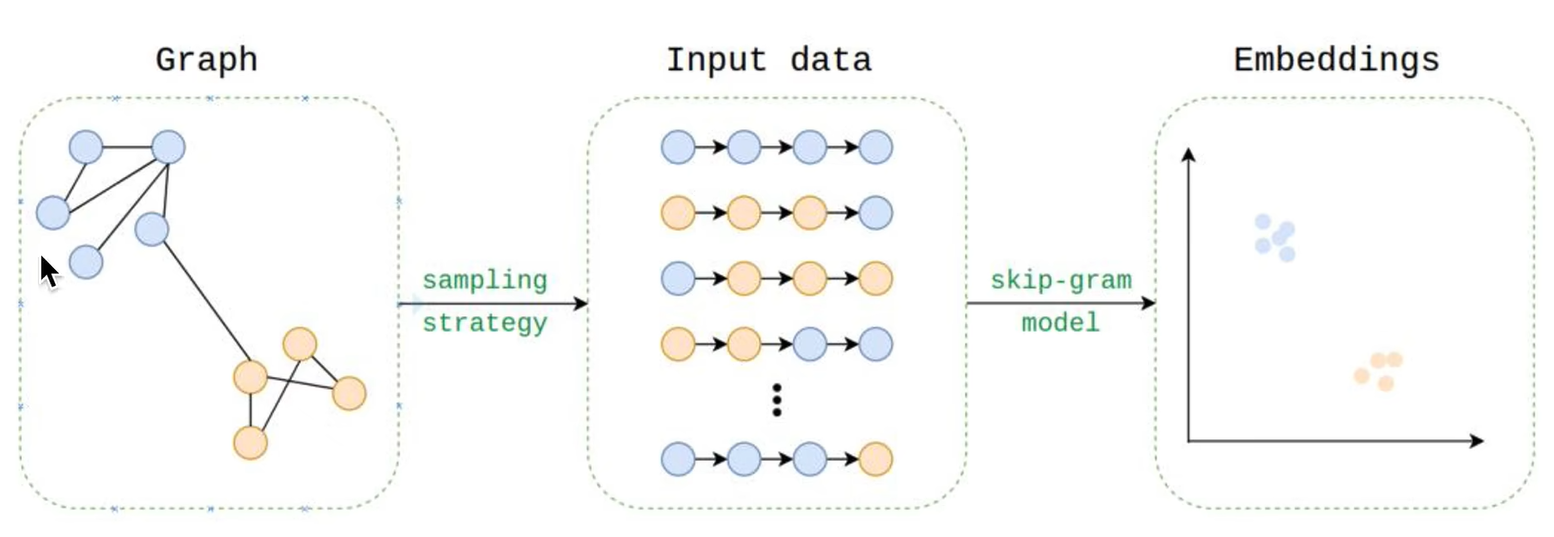
- Community aware：反映社群聚类信息，原图中相近的点嵌入后依然相近
- Low dimensional：低维度嵌入有助于防止过拟合
- Continuous：元素的细微变化都会对模型产生影响，可以拟合出一个平滑的决策边界
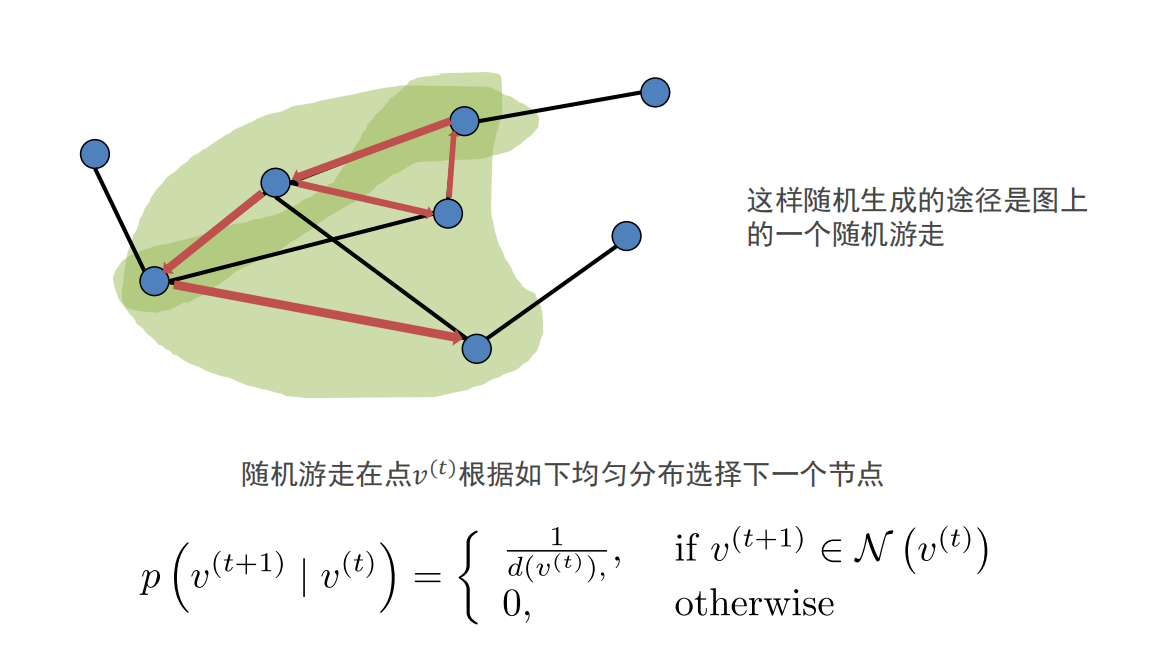
随机游走：可以使用并行方式，在线增量进行随机游走。
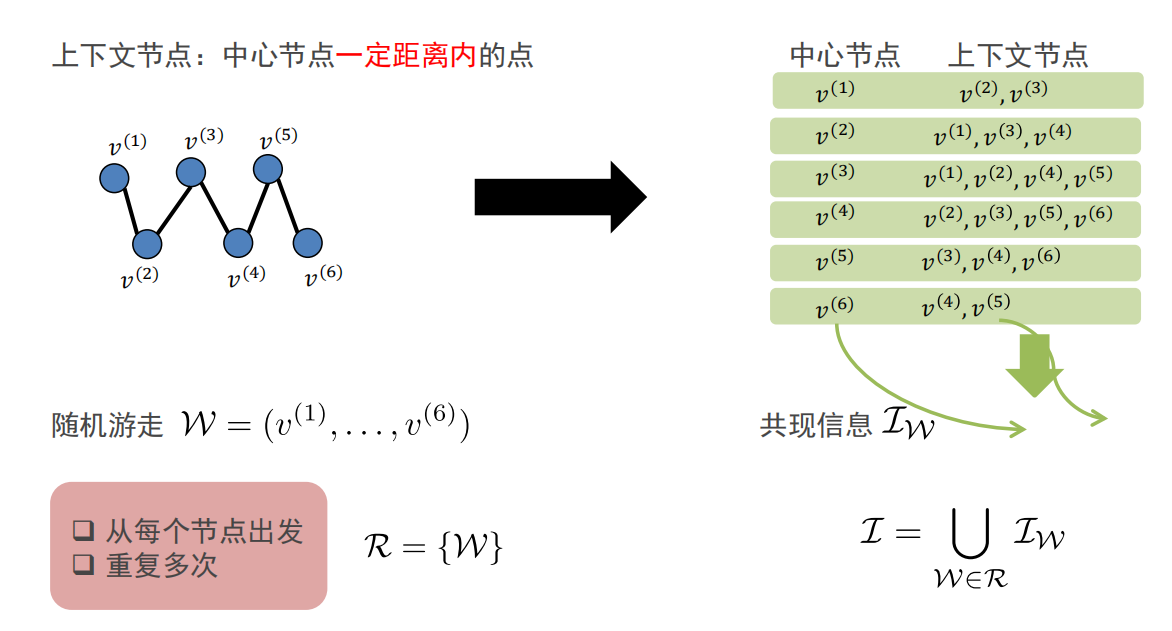
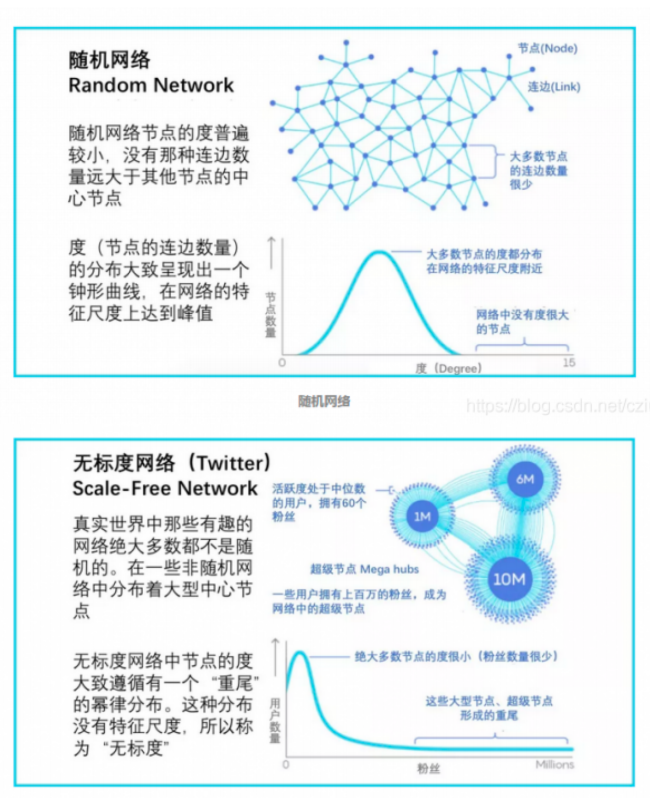
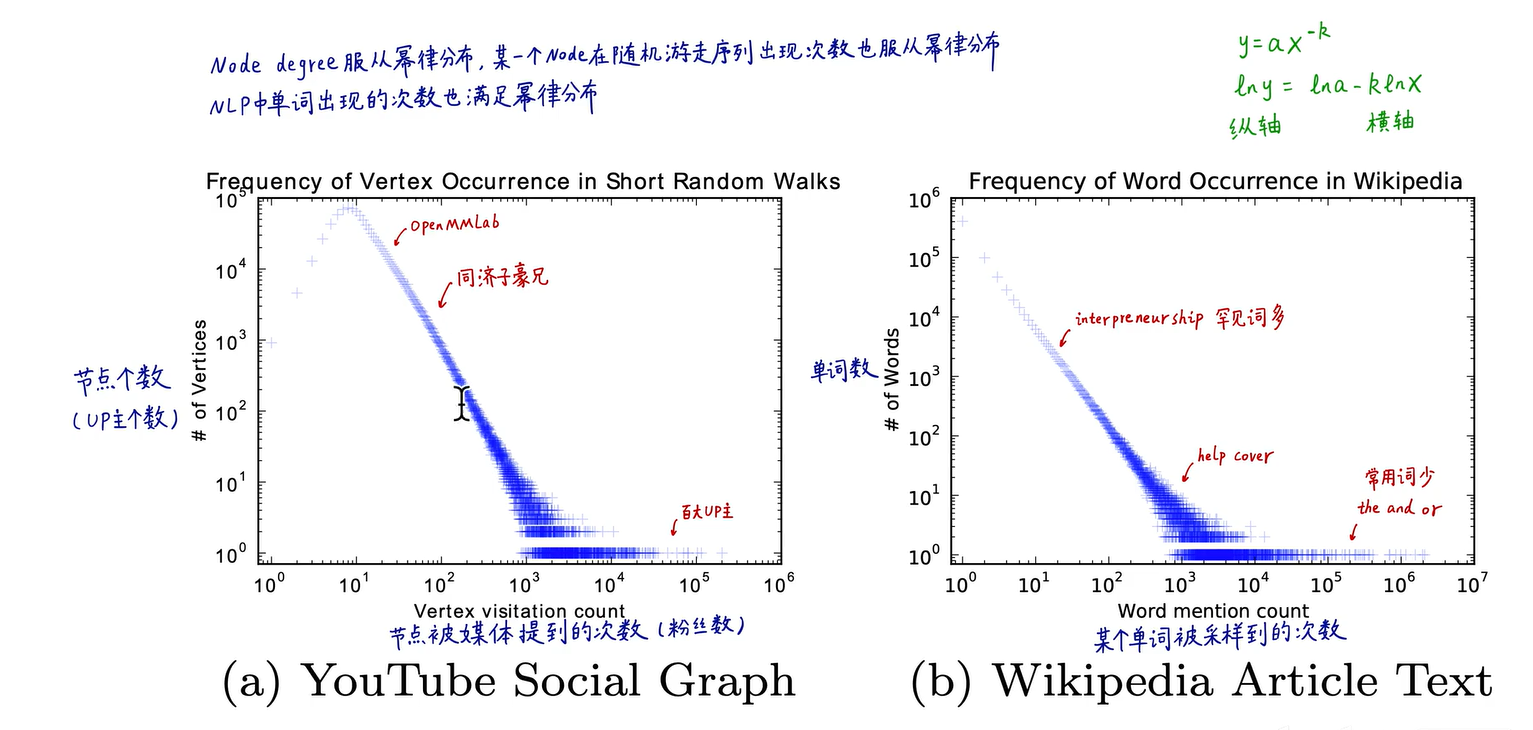
幂律分布：在一个无标度网络中，中枢节点的连接数远高于其他节点，会产生长尾现象，也称为Zipf定律（词频排序名次与词频成正比，只有极少数的词被经常使用）
语言模型: 用前 $i$ -1个词预测下文的第 $i$ 个词，通过 $Pr\left(v_{i} \mid\left(v_{1}, v_{2}, \cdots, v_{i-1}\right)\right)$ ，使用提取Embedding的函数 $\Phi$ : $\in V \mapsto R^{|V| \times d}$ ，可表示用前 $i$ -1个节点的Embedding预测第 $i$ 个节点
$Pr\left(v_{i} \mid\left(\Phi\left(v_{1}\right), \Phi\left(v_{2}\right), \cdots, \Phi\left(v_{i-1}\right)\right)\right)$

关键技术

DeepWalk
在这里插入图片描述
SkipGram算法

分层softmax：采用霍夫曼编码

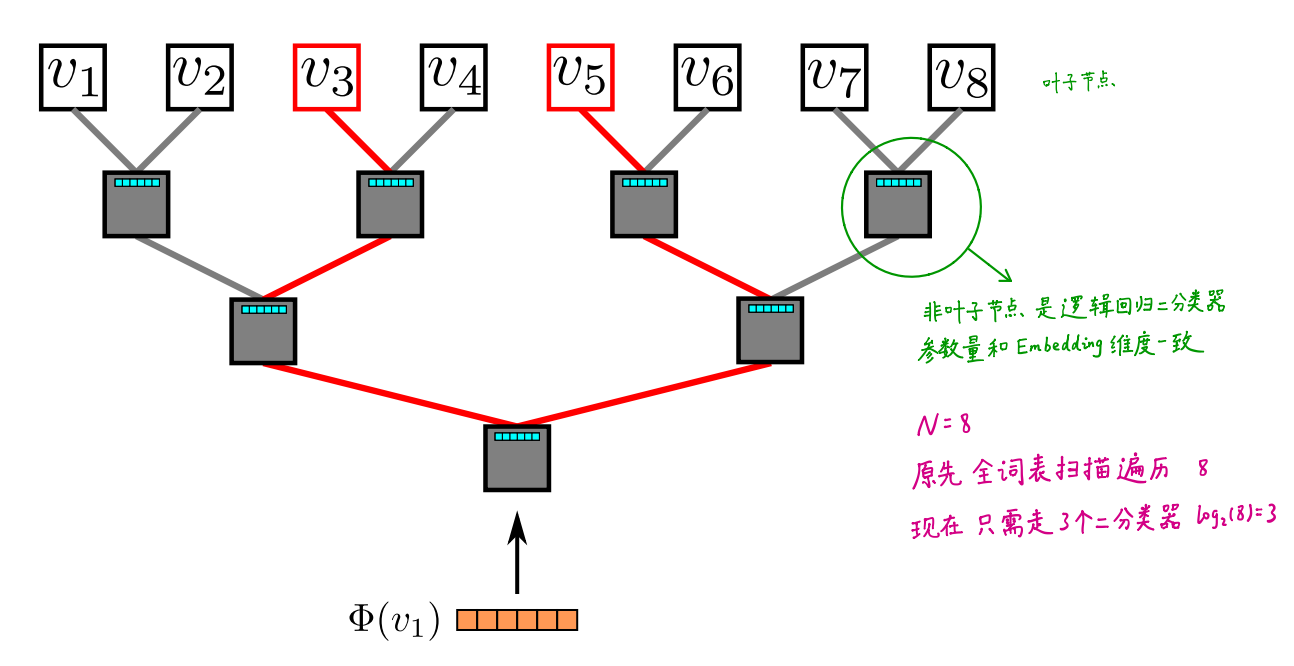
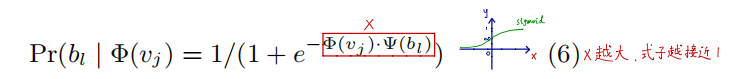
DeepWalk有两套权重

N个节点的D维Embdding
(N-1)个逻辑回归，每个有D个权重

代码实战

参考资料
https://www.analyticsvidhya.com/blog/2019/11/graph-feature-extraction-deepwalk/

https://github.com/prateekjoshi565/DeepWalk

import networkx as nx # 图数据挖掘

# 数据分析
import pandas as pd
import numpy as np

import random # 随机数
from tqdm import tqdm # 进度条

# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inline

plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签  
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号

获取维基百科网页引用关联数据

打开网站[https://densitydesign.github.io/strumentalia-seealsology](https://densitydesign.github.io/strumentalia-seealsology)
Distance设置为4
输入以下链接
https://en.wikipedia.org/wiki/Computer_vision
https://en.wikipedia.org/wiki/Deep_learning
https://en.wikipedia.org/wiki/Convolutional_neural_network
https://en.wikipedia.org/wiki/Decision_tree
https://en.wikipedia.org/wiki/Support-vector_machine
点击START CRAWLING，爬取1000个网页之后，点击STOP & CLEAR QUEUE
Download-下载TSV文件，保存至代码相同目录，命名为seealsology-data.tsv

df = pd.read_csv("seealsology-data.tsv", sep = "\t")
df.head()

在这里插入图片描述
构建无向图并进行可视化

G = nx.from_pandas_edgelist(df, "source", "target", edge_attr=True, create_using=nx.Graph())
plt.figure(figsize=(15,14))
nx.draw(G)
plt.show()

在这里插入图片描述

生成随机游走节点序列的函数

def get_randomwalk(node, path_length):
    '''
    输入起始节点和路径长度，生成随机游走节点序列
    '''
    
    random_walk = [node]
    
    for i in range(path_length-1):
        # 汇总邻接节点
        temp = list(G.neighbors(node))
        temp = list(set(temp) - set(random_walk))    
        if len(temp) == 0:
            break
        # 从邻接节点中随机选择下一个节点
        random_node = random.choice(temp)
        random_walk.append(random_node)
        node = random_node
        
    return random_walk

get_randomwalk('random forest', 5)

[‘random forest’,
‘out-of-bag error’,
‘bootstrap aggregating’,
‘cascading classifiers’,
‘boosting (meta-algorithm)’]

生成随机游走序列

gamma = 10 # 每个节点作为起始点生成随机游走序列个数
walk_length = 5 # 随机游走序列最大长度

random_walks = []

for n in tqdm(all_nodes): # 遍历每个节点
    for i in range(gamma): # 每个节点作为起始点生成gamma个随机游走序列
        random_walks.append(get_randomwalk(n, walk_length))

# 生成随机游走序列个数
len(random_walks)

85600

训练Word2Vec模型

from gensim.models import Word2Vec # 自然语言处理

model = Word2Vec(vector_size=256, # Embedding维数
                 window=4, # 窗口宽度
                 sg=1, # Skip-Gram
                 hs=0, # 不加分层softmax
                 negative=10, # 负采样
                 alpha=0.03,  # 初始学习率
                 min_alpha=0.0007, # 最小学习率
                 seed=14 # 随机数种子
                )

# 用随机游走序列构建词汇表
model.build_vocab(random_walks, progress_per=2)
# 训练（耗时1分钟左右）
model.train(random_walks, total_examples=model.corpus_count, epochs=50, report_delay=1)

分析Word2Vec结果

# 查看某个节点的Embedding
model.wv.get_vector('random forest').shape

(256,)

# 找相似词语
model.wv.similar_by_word('decision tree')

[(‘behavior tree (artificial intelligence, robotics and control)’,
0.7099794745445251),
(‘drakon’, 0.6946774125099182),
(‘decision list’, 0.6726175546646118),
(‘self-documenting code’, 0.6475881934165955),
(‘decision matrix’, 0.6162508726119995),
(‘behavior trees (artificial intelligence, robotics and control)’,
0.6040382385253906),
(‘structured programming’, 0.5988644361495972),
(‘decision-tree pruning’, 0.5983075499534607),
(‘belief structure’, 0.5966054201126099),
(‘decision tree model’, 0.5922632813453674)]

PCA降维可视化

可视化全部词条的二维Embedding

X = model.wv.vectors#(8560, 256)
# 将Embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
embed_2d = pca.fit_transform(X)#(8560, 2)

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

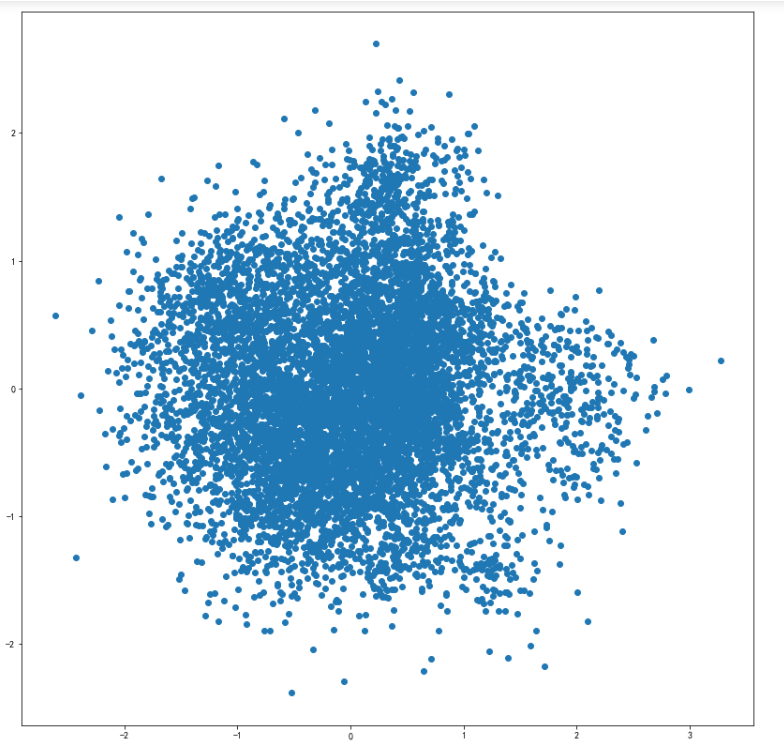
在这里插入图片描述
可视化某个词条的二维Embedding

term = 'computer vision'
term_256d = model.wv[term].reshape(1,-1)#(1, 256)
term_2d = pca.transform(term_256d)#(1, 2)

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])
plt.scatter(term_2d[:,0],term_2d[:,1],c='r',s=200)
plt.show()

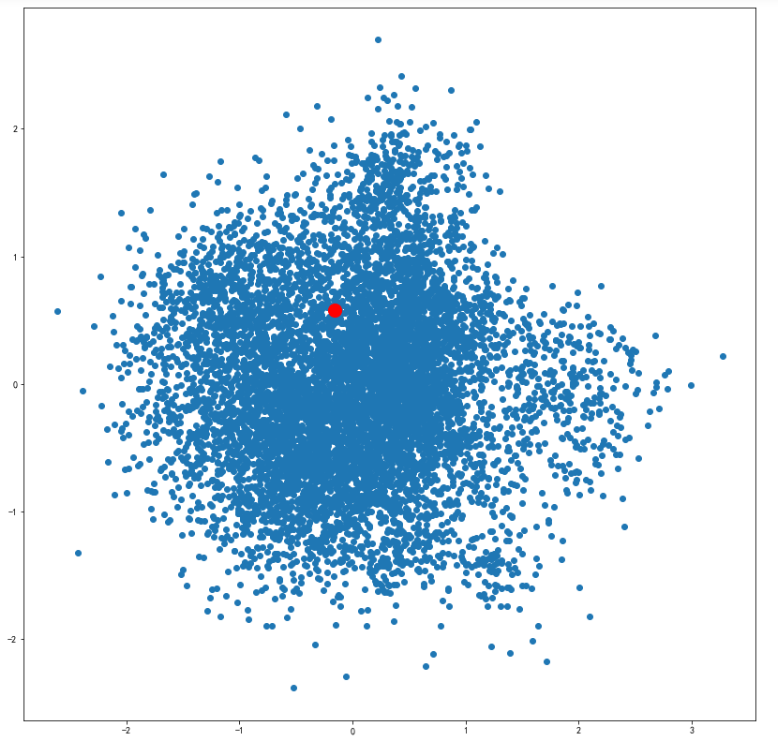
在这里插入图片描述
可视化某些词条的二维Embedding

# 计算PageRank重要度
pagerank = nx.pagerank(G)
# 从高到低排序
node_importance = sorted(pagerank.items(), key=lambda x:x[1], reverse=True)

# 取最高的前n个节点
n = 30
terms_chosen = []
for each in node_importance[:n]:
    terms_chosen.append(each[0])
    
# 输入词条，输出词典中的索引号
term2index = model.wv.key_to_index

# 可视化全部词条和关键词条的二维Embedding
plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])#绘制全部词条

for item in terms_chosen:
    idx = term2index[item]#关键词条的索引号
    plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)#绘制关键词条
    plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()

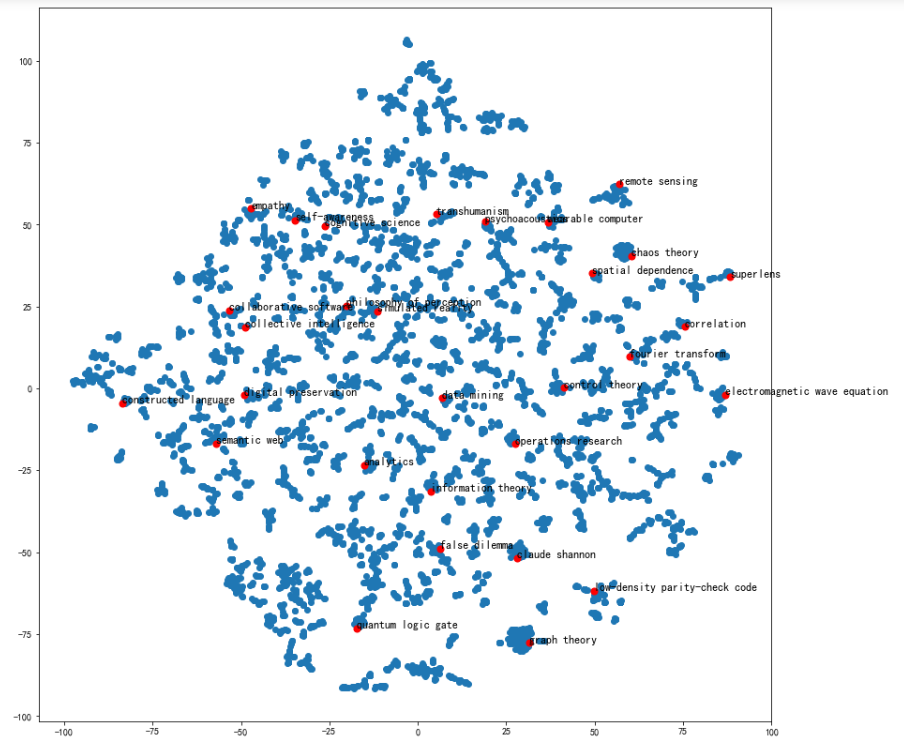
在这里插入图片描述

TSNE降维可视化

可视化全部词条的二维Embedding

# 将Embedding用TSNE降维到2维
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, n_iter=1000)
embed_2d = tsne.fit_transform(X)

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

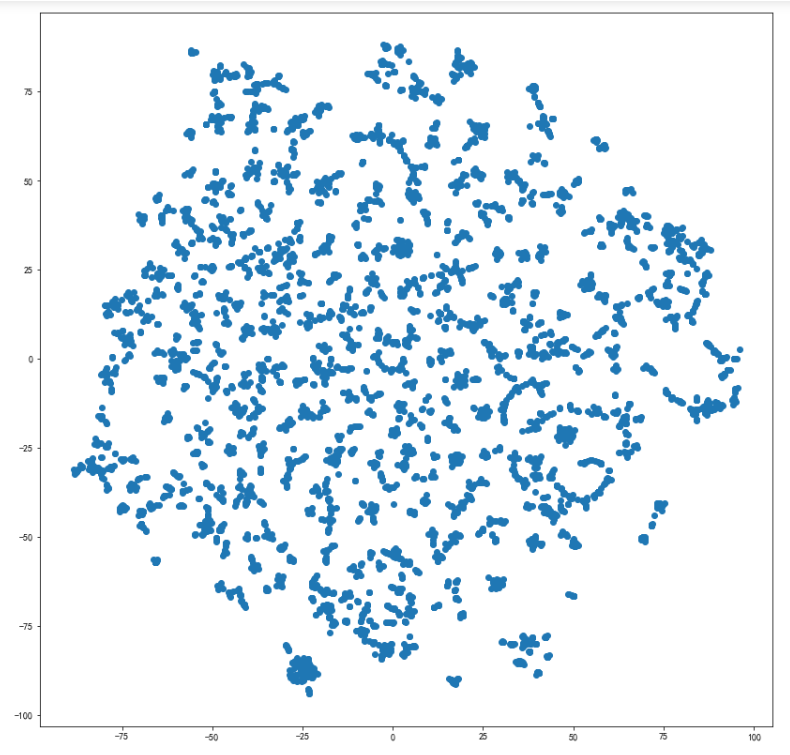
在这里插入图片描述
可视化全部词条和关键词条的二维Embedding

plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:,0], embed_2d[:,1])

for item in terms_chosen:
    idx = term2index[item]
    plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)
    plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()

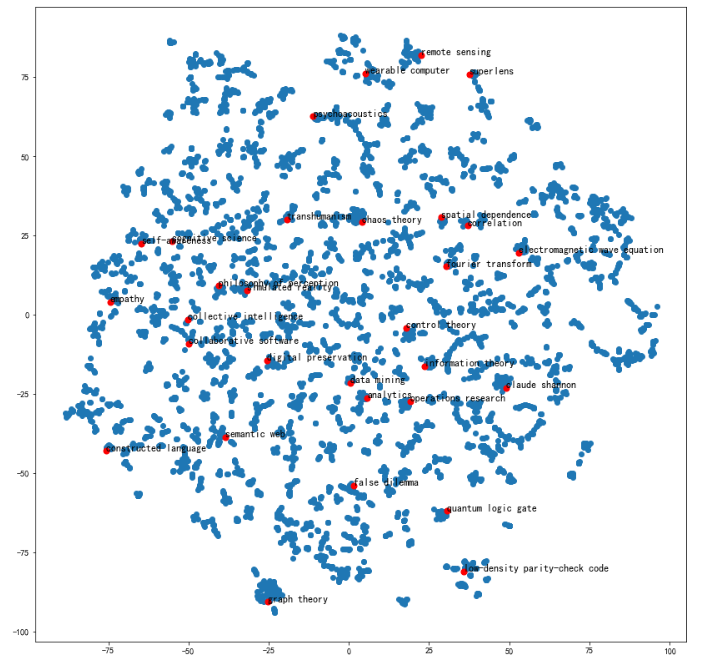
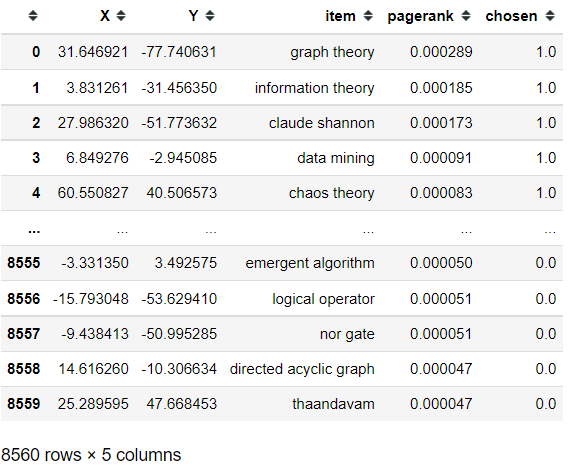
在这里插入图片描述
导出TSNE降维到二维之后的Embedding

terms_chosen_mask = np.zeros(X.shape[0])
for item in terms_chosen:
    idx = term2index[item]
    terms_chosen_mask[idx] = 1

df = pd.DataFrame()
df['X'] = embed_2d[:,0]
df['Y'] = embed_2d[:,1]
df['item'] = model.wv.index_to_key
df['pagerank'] = pagerank.values()
df['chosen'] = terms_chosen_mask

df.to_csv('tsne_vis_2d.csv',index=False)
df

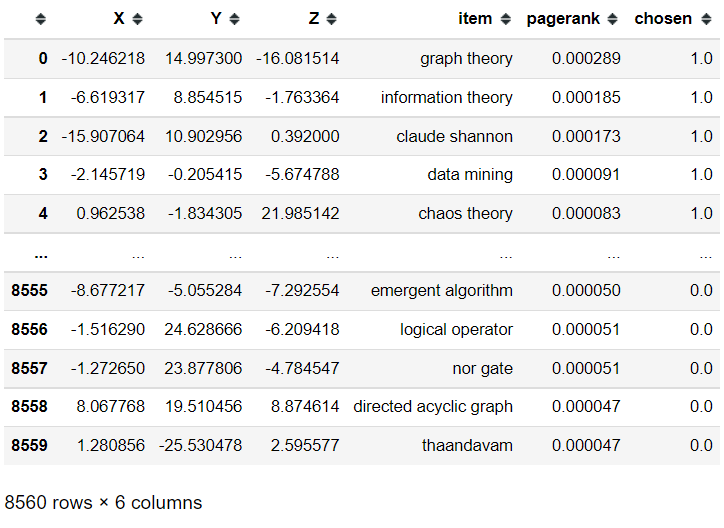
在这里插入图片描述

可视化全部词条的三维Embedding

# 将Embedding用TSNE降维到3维
from sklearn.manifold import TSNE
tsne = TSNE(n_components=3, n_iter=1000)
embed_3d = tsne.fit_transform(X)

导出TSNE降维到三维之后的Embedding

df = pd.DataFrame()
df['X'] = embed_3d[:,0]
df['Y'] = embed_3d[:,1]
df['Z'] = embed_3d[:,2]
df['item'] = model.wv.index_to_key
df['pagerank'] = pagerank.values()
df['chosen'] = terms_chosen_mask

df.to_csv('tsne_vis_3d.csv',index=False)
df

在这里插入图片描述

Node2Vec算法

DeepWalk的缺点

用完全随机游走，训练节点嵌入向量
仅能反映相邻节点的社群相似信息
无法反映节点的功能角色相似信息

Node2Vec

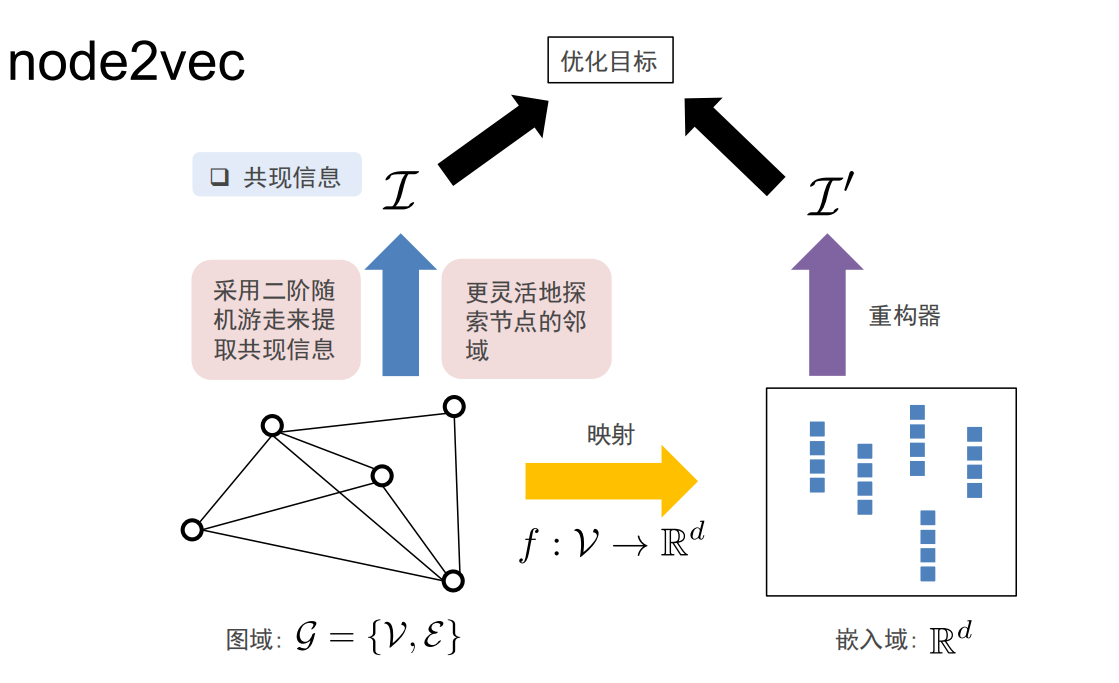
在这里插入图片描述
Node2Vec是有偏的随机游走：

超参数p控制从节点 $v^{(t-1)}$ 游走到 $v^{(t)}$ 之后立即重新访问 $v^{(t-1)}$ 的概率，p越小，越可能访问已访问的节点
超参数q允许随机游走区分“向内”和“向外”的节点，q越小，越可能访问到离已访问节点更远的节点。

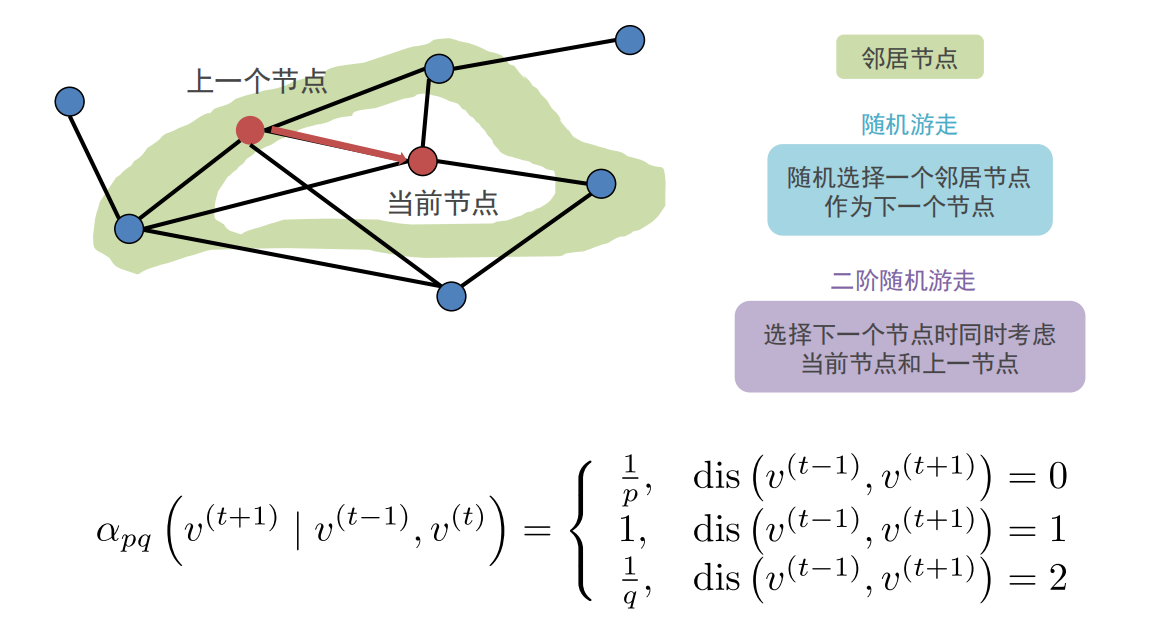
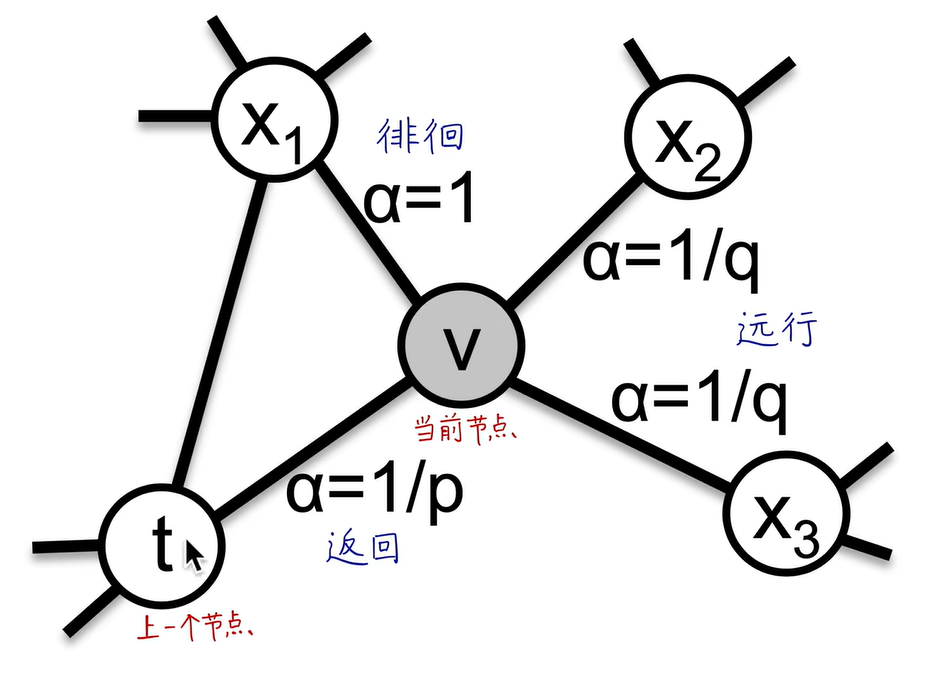
在这里插入图片描述

当p值很小时，属于广度优先搜索，反映微观的邻域
当q值很小时，属于深度优先搜索，反映宏观的视角

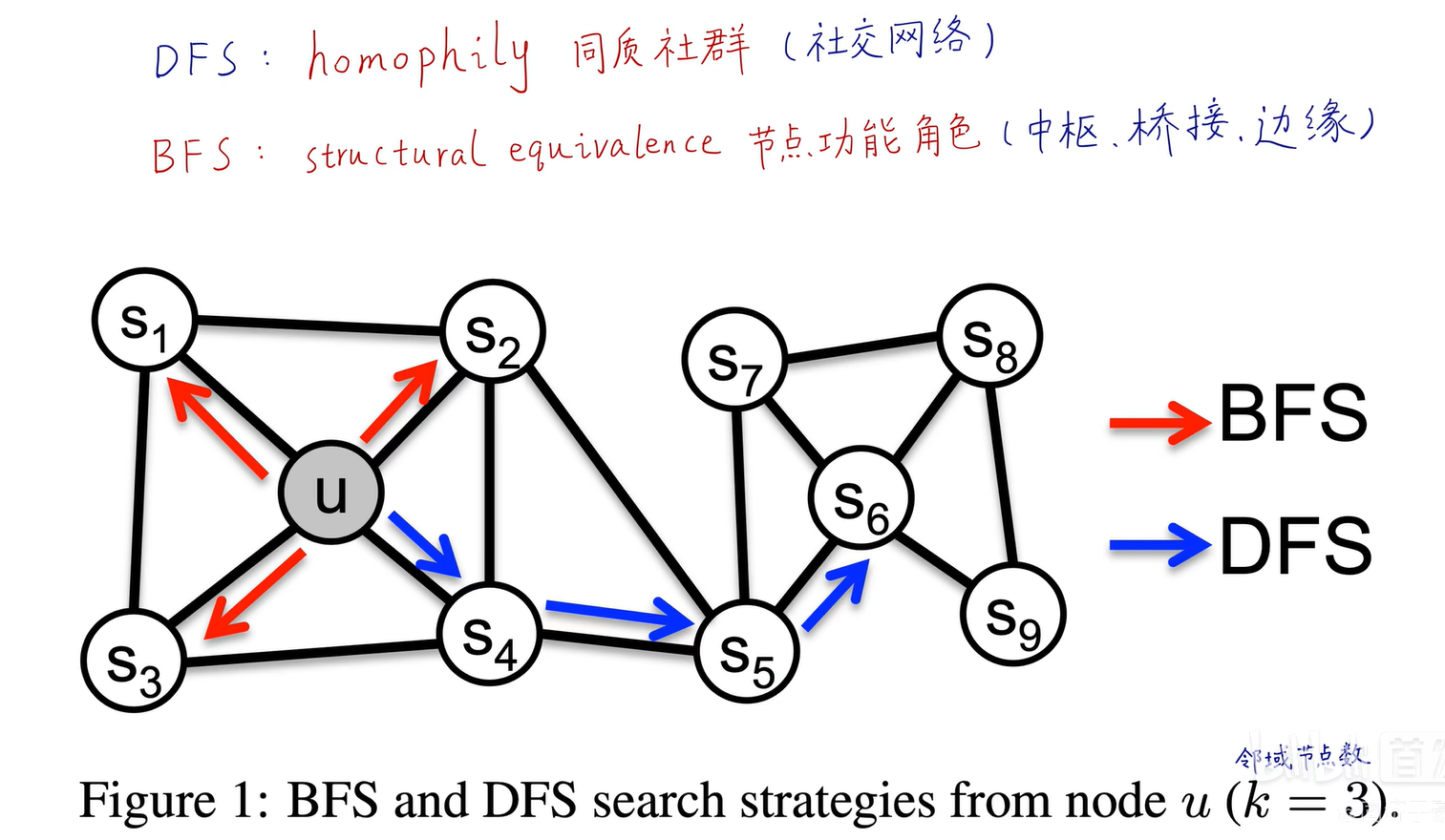
在这里插入图片描述
BFS和DFS只适合探索同质性和结构等价性的极端情况不同，现实世界中的网络常常同时表现出这两种等价性。
通过p、q参数控制的二阶随机游走，可以在BFS和DFS之间插值，从而反映不同的节点等价性概念。二阶是马尔可夫链的相关概念，表示下一节点是否被遍历不仅与**当前节点（第一阶）的拓扑结构有关，还与游走的上一个节点（第二阶）**相关
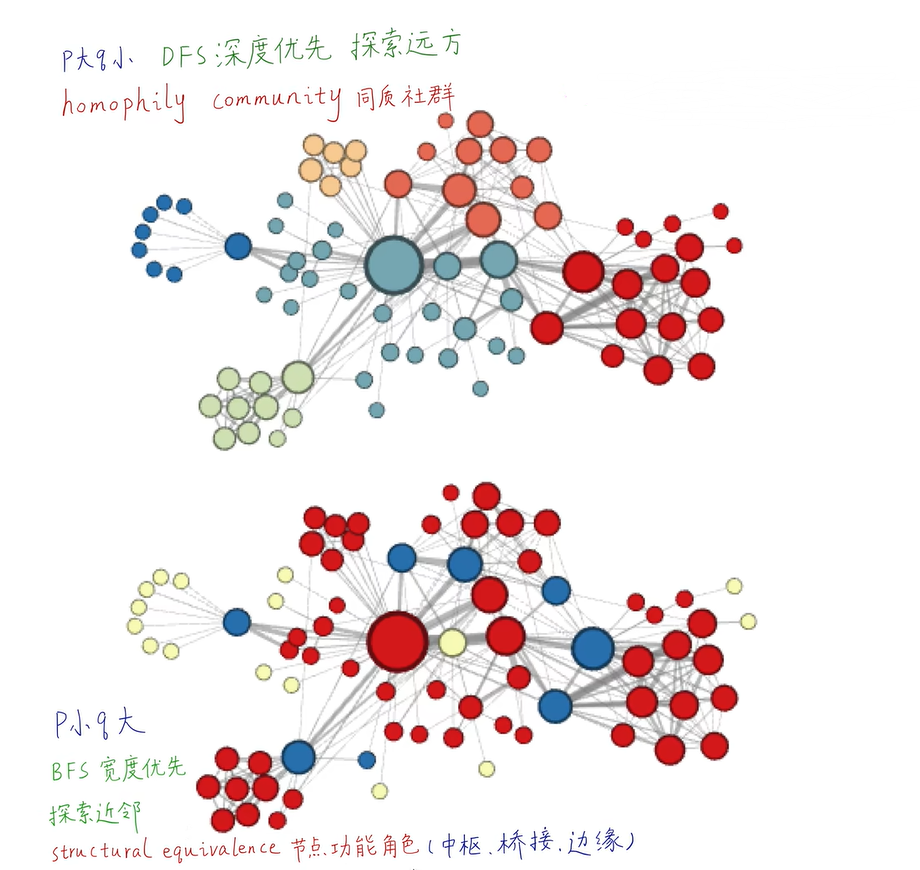
在这里插入图片描述
Node2Vec在空间和时间方面都具有较高的计算效率

空间复杂度为 $O (∣ E ∣)$
对于二阶随机游走，存储每个节点邻居之间的相互关系有助于提高采样速度，其空间复杂度为 $O(a^{2}|V|)$ ，其中 $a$ 是图的平均度数，对于实际网络来说通常很小。
时间复杂度 $O (l k (l - k))$
通过在样本生成过程中强制图的连通性，随机游走提供了一种方便的机制，通过在不同的源节点之间重复使用样本来增加有效采样率。

通过模拟长度为 $l$ 的随机游走，我们可以一次性为 $l - k$ 个节点生成 $k$ 个样本，因为随机游走具有马尔可夫性质。

关键技术

node2vecWalk
在这里插入图片描述
由于任何随机游走都有由起始节点 $u$ 选择所带来的隐含偏差，因此该算法从每个节点开始模拟 $r$ 次固定长度为 $l$ 的随机游走来消除这种偏差。

在每一步的游走过程中，节点采样是基于转移概率 $π vx$ 完成的，该概率可以预先计算。node2vec算法的三个阶段依次是：

预处理以计算转移概率，
模拟随机游走
使用SGD进行优化

每个阶段都可以并行执行，因此node2vec算法有很强的可扩展性。

Alias Sample
用于产生下一个随机游走节点，时间复杂度为 $O (1)$ ，用空间（预处理）换时间，适用于大量反复的抽样情况下，将离散分布抽样转化为均匀分布抽样
具体可以参考：https://www.cnblogs.com/Lee-yl/p/12749070.html

代码实战

import networkx as nx # 图数据挖掘
import numpy as np # 数据分析
import random # 随机数

# 数据可视化
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签  
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号

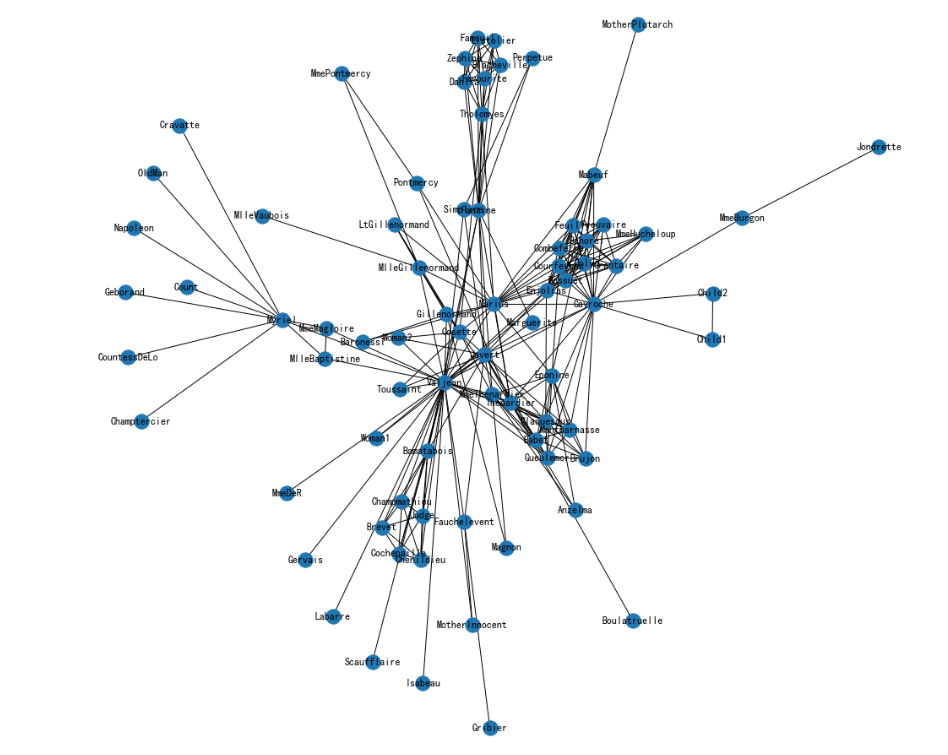
导入《悲惨世界》人物数据集并进行可视化

# 《悲惨世界》人物数据集
G = nx.les_miserables_graph()
# 可视化
plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, seed=5)
nx.draw(G, pos, with_labels=True)
plt.show()

在这里插入图片描述

构建Node2Vec模型

from node2vec import Node2Vec
# 设置node2vec参数
node2vec = Node2Vec(G, 
                    dimensions=32,  # 嵌入维度
                    p=1,            # 回家参数
                    q=3,          # 外出参数
                    walk_length=10, # 随机游走最大长度
                    num_walks=600,  # 每个节点作为起始节点生成的随机游走个数
                    workers=4       # 并行线程数
                   )

# p=1, q=0.5, n_clusters=6。DFS深度优先搜索，挖掘同质社群
# p=1, q=2, n_clusters=3。BFS宽度优先搜索，挖掘节点的结构功能。

# 训练Node2Vec，参数文档见 gensim.models.Word2Vec
model = node2vec.fit(window=3,    # Skip-Gram窗口大小
                     min_count=1,  # 忽略出现次数低于此阈值的节点（词）
                     batch_words=4 # 每个线程处理的数据量
                    )
X = model.wv.vectors

节点Embedding聚类可视化

# # DBSCAN聚类
# from sklearn.cluster import DBSCAN
# cluster_labels = DBSCAN(eps=0.5, min_samples=6).fit(X).labels_
# print(cluster_labels)

# KMeans聚类
from sklearn.cluster import KMeans
import numpy as np
cluster_labels = KMeans(n_clusters=3).fit(X).labels_
print(cluster_labels)

将networkx中的节点和词向量中的节点对应
将词汇表的节点顺序转为networkx中的节点顺序

colors = []
nodes = list(G.nodes)
for node in nodes: # 按 networkx 的顺序遍历每个节点
    idx = model.wv.key_to_index[str(node)] # 获取这个节点在 embedding 中的索引号
    colors.append(cluster_labels[idx]) # 获取这个节点的聚类结果

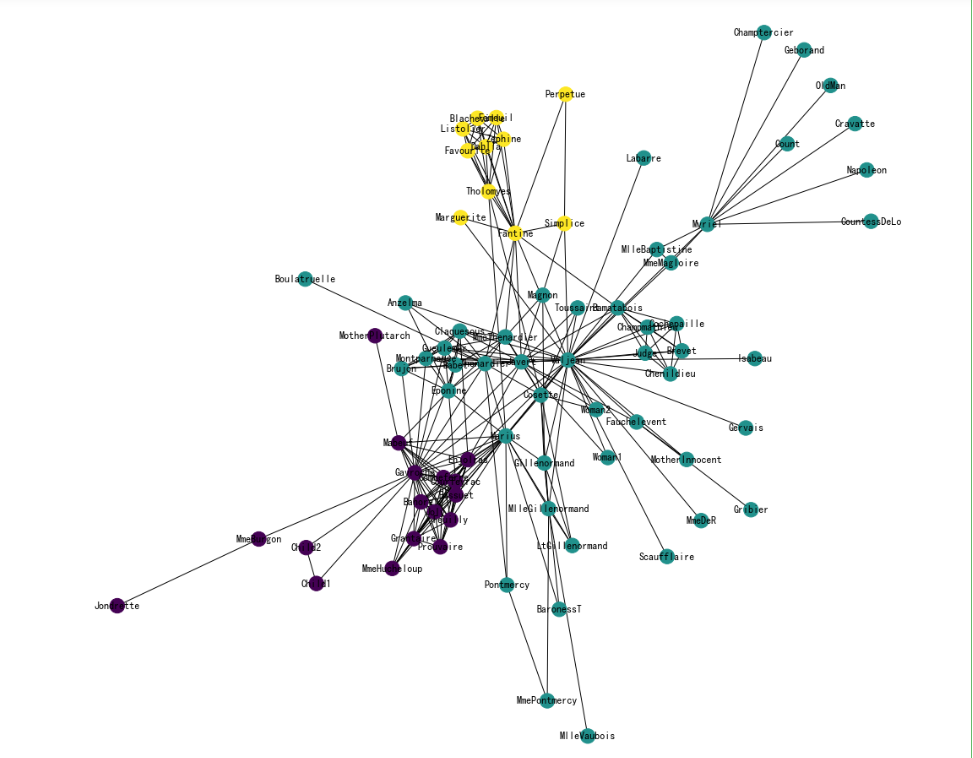
可视化聚类效果

plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos, node_color=colors, with_labels=True)
plt.show()

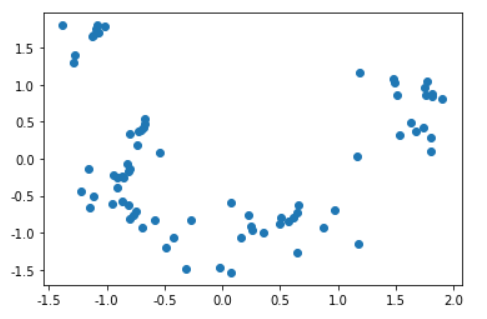
在这里插入图片描述

节点Embedding降维可视化

# 将Embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
embed_2d = pca.fit_transform(X)

# # 将Embedding用TSNE降维到2维
# from sklearn.manifold import TSNE
# tsne = TSNE(n_components=2, n_iter=5000)
# embed_2d = tsne.fit_transform(X)

# plt.figure(figsize=(14,14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

在这里插入图片描述
查看Embedding

# 查看某个节点的Embedding
model.wv.get_vector('Napoleon')
# 查找 Napoleon 节点的相似节点
model.wv.most_similar('Napoleon')
# 查看任意两个节点的相似度
model.wv.similarity('Napoleon', 'Champtercier')

对Edge（连接）做Embedding

from node2vec.edges import HadamardEmbedder
# Hadamard 二元操作符：两个 Embedding 对应元素相乘
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)

# 查看 任意两个节点连接 的 Embedding
edges_embs[('Napoleon', 'Champtercier')]

# 计算所有 Edge 的 Embedding
edges_kv = edges_embs.as_keyed_vectors()

# 查看 关系与 某两个节点 最相似的 节点对
edges_kv.most_similar(str(('Bossuet', 'Valjean')))

思考题

DeepWalk

DeepWalk本质上是在解决什么问题？
DeepWalk和Word2Vec有哪些异同？
DeepWalk和Node2Vec有哪些异同？
DeepWalk的随机游走生成过程有哪些缺点？如何改进？
DeepWalk是否包含节点的类别和自身特征信息？
除了非标度网络和自然语言外，还有哪些分布服从幂律分布？
非标度网络和随机网络有什么区别？
如果两个节点隔得非常远，DeepWalk能否捕捉这样的关系？
DeepWalk为什么在稀疏标注场景下表现地更好？
除了对节点编码，DeepWalk能否对连接、子图、全图做编码？
随机游走的序列最大长度应设置为多少合适？
DeepWalk论文中对原生DeepWalk做了哪两种改进？
DeepWalk能否解决link prediction问题？为什么？

Node2Vec

为什么DFS探索的是节点社群属性，BFS探索的是节点功能角色属性？
Node2Vec中的BFS和DFS，和大学计算机本科《数据结构与算法》课程中的BFS、DFS搜索有什么异同？
Node2Vec中的随机游走，是相对于上一个节点和当前节点，为什么不是相对于起始节点和当前节点？
论文实验结果中，为什么PPI蛋白质图数据集上，Node2Vec相比DeepWalk，性能没有显著提升？
连接如果带权重的话，如何影响有偏随机游走序列生成？
有向图和无向图，如何影响有偏随机游走序列生成？
为什么使用Alias Sampling？简述Alias Sampling的基本原理
Node2vec的BFS是否能用在分析自然语言中单词的角色（中枢单词、桥接单词）
除了DeepWalk和Node2Vec，还有哪些随机游走方法？
Node2Vec算法有哪些缺点？如何弥补？

总结

本篇文章主要讲解了DeepWalk算法和Node2Vec算法

DeepWalk算法能够通过随机游走序列（邻居信息和社群信息）学习网络的连接结构信息，将节点编码为连续地维的稠密的向量空间，新加入节点时不需要重新训练，只需要输入新节点和新连接关系，再进行增量训练，并且它可以进行并行计算。在代码实战部分，使用维基百科词条数据构建无向图，生成随机游走节点序列，训练Word2Vec模型，通过计算PageRank得到关键词条，并对embedding结果进行降维可视化。
Node2Vec通过调节p、q值，实现有偏随机游走，探索节点社群、功能等不同属性。首次把节点分类用于Link Prediction，可解释性、可扩展性好，性能卓越。但是需要大量随机游走序列训练，弱水三千取—瓢，管中窥豹，距离较远的两个节点无法直接相互影响，看不到全图信息。仅编码图的连接信息，没有利用节点的属性特征，没有真正用到神经网络和深度学习。