R-旋转操作
在量子计算中,RX, RY, RZ门是三种基本的单量子比特旋转门,它们分别绕X轴、Y轴、Z轴旋转量子比特的态矢量。
RX旋转门:绕X轴旋转角度为
θ
\theta
θ的RX门的矩阵表示为:
R
x
(
θ
)
(
c
o
s
θ
2
−
i
s
i
n
θ
2
−
i
s
i
n
θ
2
c
o
s
θ
2
)
R_x(\theta)\begin{pmatrix} cos\frac{\theta}{2}& & -isin\frac{\theta}{2} \\ -isin\frac{\theta}{2}& & cos\frac{\theta}{2} \end{pmatrix}
Rx(θ)(cos2θ−isin2θ−isin2θcos2θ)
RY旋转门:绕Y轴旋转角度为
θ
\theta
θ的RY门的矩阵表示为:
R
y
(
θ
)
(
c
o
s
θ
2
−
s
i
n
θ
2
s
i
n
θ
2
c
o
s
θ
2
)
R_y(\theta)\begin{pmatrix} cos\frac{\theta}{2}& & -sin\frac{\theta}{2} \\ sin\frac{\theta}{2}& & cos\frac{\theta}{2} \end{pmatrix}
Ry(θ)(cos2θsin2θ−sin2θcos2θ)
RZ旋转门:绕Z轴旋转角度为
θ
\theta
θ的RZ门的矩阵表示为:
R
z
(
θ
)
(
e
−
i
θ
2
0
0
e
i
θ
2
)
R_z(\theta)\begin{pmatrix} e^{-i\frac{\theta}{2}}& & 0 \\ 0& & e^{i\frac{\theta}{2}} \end{pmatrix}
Rz(θ)(e−i2θ00ei2θ)
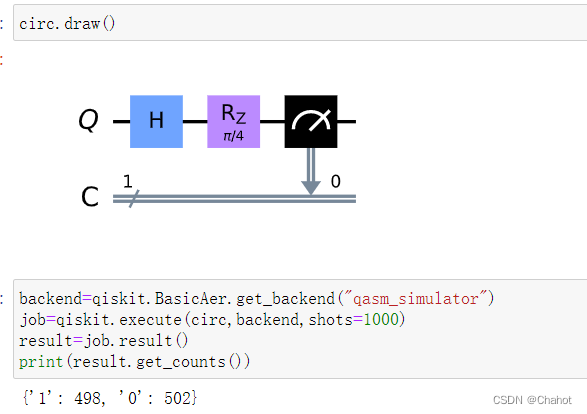
对量子态 ∣ 0 ⟩ |0\rangle ∣0⟩的 π π π旋转
对一个单量子比特进行R旋转门操作,旋转角度为
π
\pi
π,最终输出态表示如下:
RX旋转门:绕X轴旋转角度为
π
\pi
π的RX门的矩阵表示为:
R
x
(
π
)
(
c
o
s
π
2
−
i
s
i
n
π
2
−
i
s
i
n
π
2
c
o
s
π
2
)
=
1
2
(
1
−
i
−
i
1
)
R_x(\pi)\begin{pmatrix} cos\frac{\pi}{2}& & -isin\frac{\pi}{2} \\ -isin\frac{\pi}{2}& & cos\frac{\pi}{2} \end{pmatrix}=\frac{1}{\sqrt2}\begin{pmatrix} 1& & -i\\ -i& & 1 \end{pmatrix}
Rx(π)(cos2π−isin2π−isin2πcos2π)=21(1−i−i1)
1
2
(
1
−
i
−
i
1
)
∣
0
⟩
=
1
2
(
1
−
i
−
i
1
)
1
2
(
1
0
)
=
1
2
(
1
−
i
)
=
1
2
(
∣
0
⟩
−
i
∣
1
⟩
)
\frac{1}{\sqrt2}\begin{pmatrix} 1& & -i\\ -i& & 1 \end{pmatrix}|0\rangle=\frac{1}{\sqrt2}\begin{pmatrix} 1& & -i\\ -i& & 1 \end{pmatrix}\frac{1}{\sqrt2}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\frac{1}{\sqrt2}\begin{pmatrix} 1 \\ -i \end{pmatrix}=\frac{1}{\sqrt2}(|0\rangle-i|1\rangle)
21(1−i−i1)∣0⟩=21(1−i−i1)21(10)=21(1−i)=21(∣0⟩−i∣1⟩)
RY旋转门:绕Y轴旋转角度为
π
\pi
π的RY门的矩阵表示为:
R
y
(
π
)
∣
0
⟩
=
(
c
o
s
π
2
−
s
i
n
π
2
s
i
n
π
2
c
o
s
π
2
)
∣
0
⟩
=
(
0
−
1
1
0
)
(
1
0
)
=
(
0
1
)
=
∣
1
⟩
R_y(\pi)|0\rangle=\begin{pmatrix} cos\frac{\pi}{2}& & -sin\frac{\pi}{2} \\ sin\frac{\pi}{2}& & cos\frac{\pi}{2} \end{pmatrix}|0\rangle=\begin{pmatrix} 0& & -1 \\ 1& & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0\\ 1 \end{pmatrix}=|1\rangle
Ry(π)∣0⟩=(cos2πsin2π−sin2πcos2π)∣0⟩=(01−10)(10)=(01)=∣1⟩
RZ旋转门:绕Z轴旋转角度为
π
\pi
π的RZ门的矩阵表示为:
R
z
(
π
)
∣
0
⟩
=
(
e
−
i
π
2
0
0
e
i
π
2
)
(
1
0
)
=
(
0
e
i
π
2
)
=
e
i
π
2
∣
1
⟩
=
−
i
∣
1
⟩
R_z(\pi)|0\rangle=\begin{pmatrix} e^{-i\frac{\pi}{2}}& & 0 \\ 0& & e^{i\frac{\pi}{2}} \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ e^{i\frac{\pi}{2}} \end{pmatrix}=e^{i\frac{\pi}{2}}|1\rangle=-i|1\rangle
Rz(π)∣0⟩=(e−i2π00ei2π)(10)=(0ei2π)=ei2π∣1⟩=−i∣1⟩
根据欧拉公式
e
i
θ
=
c
o
s
θ
+
i
s
i
n
θ
e^{i\theta}=cos\theta+isin\theta
eiθ=cosθ+isinθ
代入对应公式可得
e
i
π
2
=
0
+
i
=
i
e^{i\frac{\pi}{2}}=0+i=i
ei2π=0+i=i
弧度(radians)和角度(degrees)是表示角度大小的两种不同的方式。它们之间的转换公式为:
从角度转换到弧度: θ r a d = θ d e g ⋅ π 180 \theta_{rad} = \theta_{deg} \cdot \frac{\pi}{180} θrad=θdeg⋅180π
从弧度转换到角度: θ d e g = θ r a d ⋅ 180 π \theta_{deg} = \theta_{rad} \cdot \frac{180}{\pi} θdeg=θrad⋅π180
其中, θ r a d \theta_{rad} θrad 表示弧度, θ d e g \theta_{deg} θdeg 表示角度。例如,如果要将 6 0 ∘ 60^\circ 60∘ 转换为弧度,可以使用上述公式进行计算:
θ r a d = 6 0 ∘ ⋅ π 180 = π 3 \theta_{rad} = 60^\circ \cdot \frac{\pi}{180} = \frac{\pi}{3} θrad=60∘⋅180π=3π
因此, 6 0 ∘ 60^\circ 60∘ 转换为弧度为 π 3 \frac{\pi}{3} 3π。同样地,如果要将 π 4 \frac{\pi}{4} 4π 转换为角度,可以使用上述公式进行计算:
θ d e g = π 4 ⋅ 180 π = 4 5 ∘ \theta_{deg} = \frac{\pi}{4} \cdot \frac{180}{\pi} = 45^\circ θdeg=4π⋅π180=45∘
因此, π 4 \frac{\pi}{4} 4π 转换为角度为 4 5 ∘ 45^\circ 45∘。
实战应用
ex)
初始态为
∣
+
⟩
=
1
2
(
∣
0
⟩
+
∣
1
⟩
)
|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
∣+⟩=21(∣0⟩+∣1⟩),对其分别进行 三态旋转门操作,旋转角度为
4
5
∘
45^\circ
45∘,即
π
4
\frac{\pi}{4}
4π 弧度,它们的输出态是?
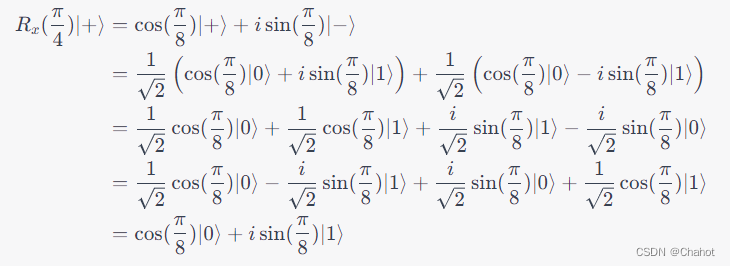
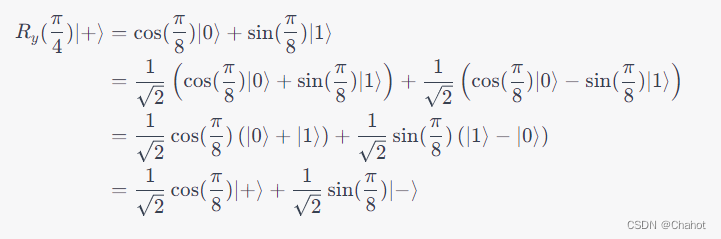
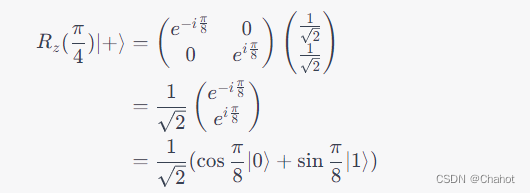
解析
假设旋转角度为 θ \theta θ,则 R z ( θ ) R_z(\theta) Rz(θ) 门的矩阵形式为:
R z ( θ ) = ( e − i θ 2 0 0 e i θ 2 ) R_z(\theta) = \begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{pmatrix} Rz(θ)=(e−i2θ00ei2θ)
初始态为 ∣ − ⟩ = 1 2 ( 1 − 1 ) |-\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix} ∣−⟩=21(1−1) 的量子比特经过一个 R z ( θ ) R_z(\theta) Rz(θ) 门后,其输出量子态为:
R z ( θ ) ∣ − ⟩ = ( e − i θ 2 0 0 e i θ 2 ) 1 2 ( 1 − 1 ) = 1 2 ( e − i θ 2 − e i θ 2 ) \begin{aligned} R_z(\theta)|-\rangle &= \begin{pmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \end{pmatrix} \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ -1 \end{pmatrix} \ &= \frac{1}{\sqrt{2}}\begin{pmatrix} e^{-i\frac{\theta}{2}} \\ -e^{i\frac{\theta}{2}} \end{pmatrix} \end{aligned} Rz(θ)∣−⟩=(e−i2θ00ei2θ)21(1−1) =21(e−i2θ−ei2θ)
因此,初始态为 ∣ − ⟩ |-\rangle ∣−⟩ 的量子比特经过一个 R z ( θ ) R_z(\theta) Rz(θ) 门后的输出量子态为 1 2 ( e − i θ 2 − e i θ 2 ) \frac{1}{\sqrt{2}}\begin{pmatrix} e^{-i\frac{\theta}{2}} \\ -e^{i\frac{\theta}{2}} \end{pmatrix} 21(e−i2θ−ei2θ)。
公式中的
R
z
(
45
°
)
R_z(45°)
Rz(45°)
e
i
θ
=
cos
θ
+
i
sin
θ
=
1
2
−
1
2
i
e^{i\theta} = \cos{\theta} + i\sin{\theta}=\frac{1}{\sqrt2}-\frac{1}{\sqrt2}i
eiθ=cosθ+isinθ=21−21i
e i θ = cos θ + i sin θ = 1 2 + 1 2 i e^{i\theta} = \cos{\theta} + i\sin{\theta}=\frac{1}{\sqrt2}+\frac{1}{\sqrt2}i eiθ=cosθ+isinθ=21+21i
R z ( θ ) ∣ − ⟩ = 1 2 ( 1 2 − 1 2 i ) ∣ 0 ⟩ − 1 2 ( 1 2 + 1 2 i ) ∣ 1 ⟩ = 1 2 ( 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) − 1 2 i ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ) = 1 2 ∣ − ⟩ − i 1 2 ∣ + ⟩ R_z(\theta)|-\rangle =\frac{1}{\sqrt2}(\frac{1}{\sqrt2}-\frac{1}{\sqrt2}i)|0\rangle-\frac{1}{\sqrt2}(\frac{1}{\sqrt2}+\frac{1}{\sqrt2}i)|1\rangle \\ =\frac{1}{\sqrt2}( \frac{1}{\sqrt2}(|0\rangle-|1\rangle)-\frac{1}{\sqrt2}i(|0\rangle+|1\rangle)) \\ =\frac{1}{\sqrt2}|-\rangle-i\frac{1}{\sqrt2}|+\rangle Rz(θ)∣−⟩=21(21−21i)∣0⟩−21(21+21i)∣1⟩=21(21(∣0⟩−∣1⟩)−21i(∣0⟩+∣1⟩))=21∣−⟩−i21∣+⟩
因此,当测量发生时,有二分之一的概率落到两种混合态上,而每种混合态还有两种不同的概率使测量得到0或者1。结果而言得到0和1的概率各为50%,但是其中同样是得到0状态,其来源可能来自于不同的混合态。