01：买卖股票的最佳时机

题目描述：
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

题解：

# 一次遍历
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        min_price = float('inf')
        max_profit = 0

        for price in prices:
            min_price = min(min_price, price)
            max_profit = max(max_profit, price - min_price)

        return max_profit

---

02：合并两个有序数组

题目描述：
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意： 最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例：
输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]

题解：

# 逆向双指针
class Solution:
    def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
        """
        Do not return anything, modify nums1 in-place instead.
        """
        p1, p2 = m - 1, n - 1
        tail = m + n - 1
        while p1 >= 0 or p2 >= 0:
            if p1 == -1:
                nums1[tail] = nums2[p2]
                p2 -= 1
            elif p2 == -1:
                nums1[tail] = nums1[p1]
                p1 -= 1
            elif nums1[p1] > nums2[p2]:
                nums1[tail] = nums1[p1]
                p1 -= 1
            else:
                nums1[tail] = nums2[p2]
                p2 -= 1
            tail -= 1

03：三数之和

题目描述：
给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

分析：
输入：
输出：
解释：

题解：

# 双指针
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        # 数组为空或者长度小于 3 退出
        if not nums or n < 3:
            return []

        nums.sort()
        # 升序排列
        res = []
        # 遍历每个元素
        for i in range(n):
            # 已经排序，最小的数一定小于 0
            if nums[i] > 0:
                break
            if i > 0 and nums[i] == nums[i-1]:
                continue

            # 双指针，对后面的元素进行搜索
            L = i + 1
            R = n - 1
            while L < R:
                # 满足条件
                if nums[i] + nums[L] + nums[R] == 0:
                    res.append([nums[i], nums[L], nums[R]])
                    while L < R and nums[L] == nums[L+1]:
                        L = L + 1
                    while L < R and nums[R] == nums[R-1]:
                        R = R - 1
                    L = L + 1
                    R = R - 1
                elif nums[i] + nums[L] + nums[R] > 0:
                    R = R - 1
                else:
                    L = L + 1

        return res

04：找出字符串中第一个匹配项的下标

题目描述：
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例：
输入：haystack = "sadbutsad", needle = "sad"
输出：0

题解：

# KMP
class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        n1 = len(needle)
        n2 = len(haystack)
        if n1 == 0:
            return 0

        next = self.getnext(n1, needle)
        p = -1
        for j in range(n2):
            while p >= 0 and needle[p + 1] != haystack[j]:
                p = next[p]
            if needle[p + 1] == haystack[j]:
                p += 1
            if p == n1 - 1:
                return j - n1 + 1

        return -1


    def getnext(self, n, needle):
        next = ['' for i in range(n)]
        k = -1
        next[0] = k
        for i in range(1, len(needle)):
            while k > -1 and needle[k + 1] != needle[i]:
                k = next[k]
            if needle[k + 1] == needle[i]:
                k += 1
            next[i] = k
        return next

05：全排列

题目描述：
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

题解：

# 回溯算法
class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        def backtrack(nums, tmp):
            if not nums:
                res.append(tmp)
                return
            for i in range(len(nums)):
                backtrack(nums[:i] + nums[i+1:], tmp + [nums[i]])

        backtrack(nums, [])
        return res

06：用队列实现栈

题目描述：
请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：
输入：
["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]
解释：

MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

题解：

import collections


class MyStack:

    def __init__(self):
        self.queue1 = collections.deque()
        self.queue2 = collections.deque()


    def push(self, x: int) -> None:
        self.queue2.append(x)
        while self.queue1:
            self.queue2.append(self.queue1.popleft())
        self.queue1, self.queue2 = self.queue2, self.queue1


    def pop(self) -> int:
        return self.queue1.popleft()


    def top(self) -> int:
        return self.queue1[0]


    def empty(self) -> bool:
        return not self.queue1



# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()

07：加一

题目描述：
给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储 单个 数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例：
输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

题解：

# 从后往前依次判断
class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        res = []
        while digits and digits[-1] == 9:
            digits.pop()
            res.append(0)
        if not digits:
            return [1] + res
        else:
            digits[-1] += 1
            return digits + res

08：电话号码的字母组合

题目描述：
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例：
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

题解：

# 递归
class Solution:
    def letterCombinations(self, digits: str) -> List[str]:

        if not digits:
            return []

        dic = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
               '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
        res = []

        def dfs(string, index):
            if index == len(digits):
                res.append(string)
                return

            num = digits[index]
            letters = dic[num]

            for i in letters:
                dfs(string + i, index + 1)

        dfs('', 0)
        
        return res

09：盛最多水的容器

题目描述：
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：

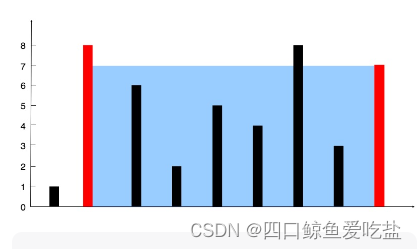
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

题解：

# 双指针
class Solution:
    def maxArea(self, height: List[int]) -> int:
        left, right = 0, len(height) - 1
        res = 0
        while left < right:
            area = min(height[left], height[right]) * (right - left)
            res = max(res, area)
            if height[left] <= height[right]:
                left += 1
            else:
                right -= 1

        return res

10：二叉树的最大深度

题目描述：
给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
输入：[3,9,20,null,null,15,7]
输出：3

题解：

# 深度优先搜索
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        else:
            left_height = self.maxDepth(root.left)
            right_height = self.maxDepth(root.right)
            return max(left_height, right_height) + 1