题目：
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：
1.首先找到需要删除的节点；
2.如果找到了，删除它。

大致思路：先用pre和T遍历分别找到要删除的结点的父结点和要删除的结点，遍历之后可分为以下几种情况：
1.要删除的结点是根节点
2.要删除的几点不是根节点
2.1要删除的结点是pre的右子树
2.1.1要删除的结点的右子树非空
2.1.2要删除的结点的右子树为空
2.2要删除的结点是pre的左子树
2.2.1要删除的结点的右子树非空
2.2.2要删除的结点的右子树为空

为什么会有这么多种情况呢？或者说为什么最后总要判断右子树为空呢？

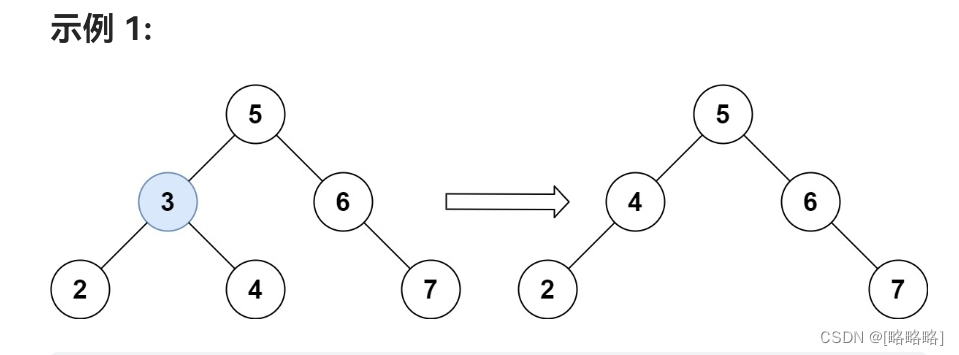
我们可以看一下题目给的例子。要删除3结点，那么pre就是5结点，此时3结点是5结点的左子树，即上面的2.2。
现在我们假设右子树为空，即如果现在没有这个4，那我们直接拿2这一子树作为pre（5）的左子树接上就可以了。
而现在有4这一子树，即右子树非空。由于右子树>根节点>左子树，所以肯定得把4这一子树作为5的左子树接上。至于2子树接在哪，我们得先遍历找到4子树最左下的结点（这一结点是4子树中值最小的结点，但由于右子树>根节点>左子树这一性质，作为曾经3的左右子树内的结点，4子树中值最小的结点的值也会比2子树中值最大的结点的值大），将2子树作为上面提到的最左下的结点的左子树接入。
至于2.1，则思路类似，只是左右需要作些更改，不再赘述。

struct TreeNode* deleteNode(struct TreeNode* root, int key){
    struct TreeNode* T=root;
    struct TreeNode* pre=NULL;
    if(root==NULL)
        return NULL;
    while(T!=NULL&&T->val!=key){
        if(T->val>key){
            pre=T;
            T=T->left;
        }
        else if(T->val<key){
            pre=T;
            T=T->right;
        }
    }
    //以上遍历找到要删除的结点T和该结点的前一个结点pre
    
    if(T!=NULL&&T->val==key){
        if(pre==NULL){//前一个结点为空，即要删除的是根节点
            if(T->right==NULL){//右子树为空
                root=T->left;
                free(T);
            }            
            else{//右子树非空
                root=T->right;
                struct TreeNode* l=root;
                while(l->left!=NULL)
                    l=l->left;
                l->left=T->left;
                free(T);   
            }
        }
     
        else{//要删除的不是根节点
            if(T->val>pre->val){//前一个结点的值小于要删除结点的值，即要删除的是pre的右子树
                if(T->right!=NULL){//T的右子树非空
                    struct TreeNode* l=T->right;
                    while(l->left!=NULL)//寻找T右子树的最左下结点
                        l=l->left;
                     l->left=T->left;//T的左子树接在右子树最左下结点上
                    pre->right=T->right;//将T的右子树接在pre的右子树位置上
                    free(T);
                }
                else{//右子树为空
                    pre->right=T->left;
                    free(T);
                }            
            }
            else{//要删除的是pre的左子树
                if(T->right!=NULL){//T的右子树非空
                    struct TreeNode* l=T->right;
                    while(l->left!=NULL)//遍历找到最左下结点
                        l=l->left;
                    l->left=T->left;//T的左子树接在T右子树的最左下结点
                    pre->left=T->right;//T的右子树接在pre的左子树位置上
                    free(T);
                 }
                else{//右子树为空
                    pre->left=T->left;
                    free(T);
                }      
            }
        }        
    }
    
    return root;
}