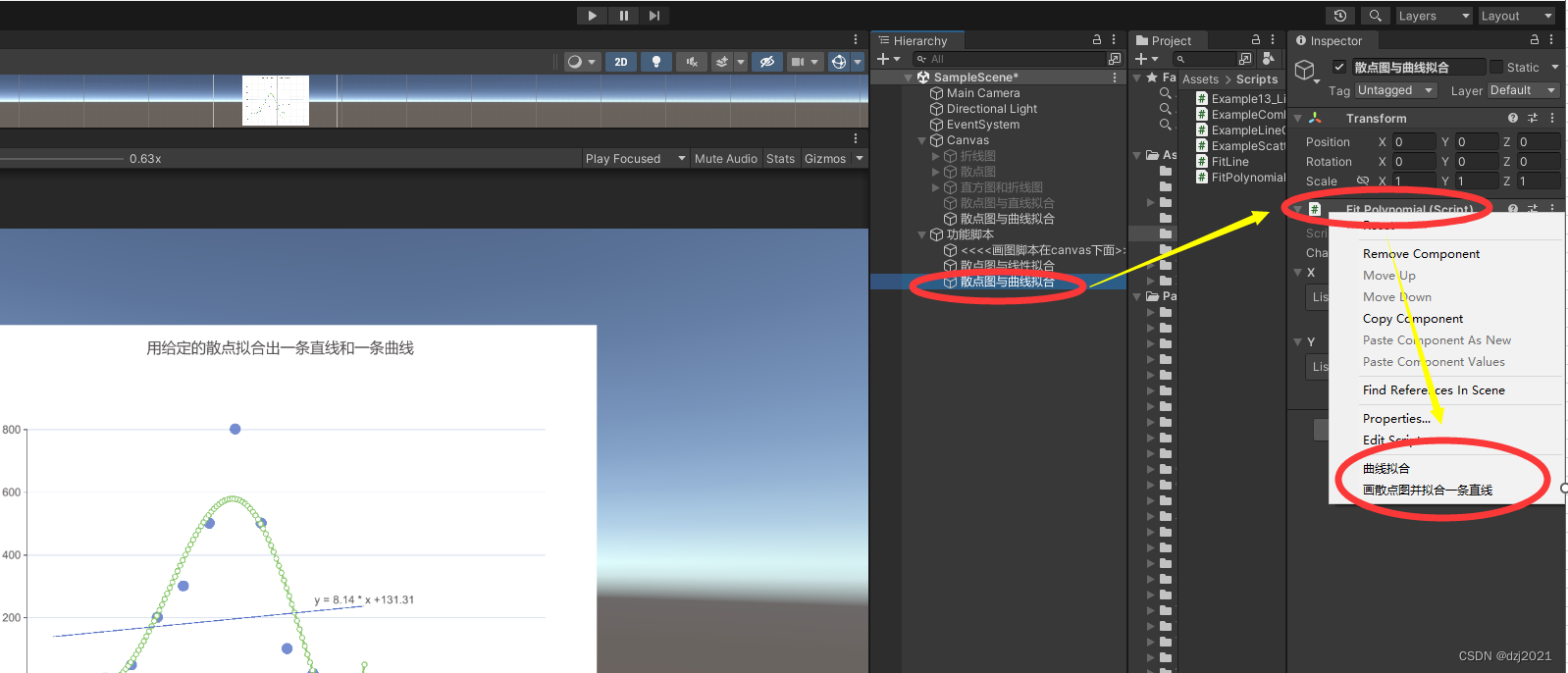
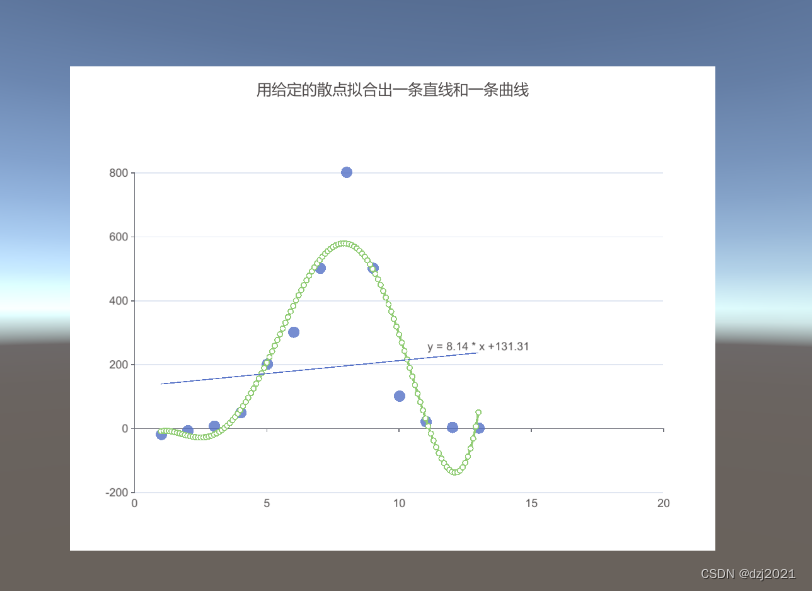
一、散点数据、拟合直线、拟合曲线
- 蓝色圆点是数据样本
- 直线为拟合的直线
- 曲线是拟合出来的曲线
二、C#中曲线拟合的实现
- 0、曲线拟合的一般步骤(以平面坐标XY为例)
【1】给定计算拟合的阶数k,k的取值最大为【样本个数-1】
【2】计算出拟合参数列表
【3】给定一个x值,用拟合参数计算对应的y值
【4】计算所有的y值
注意:拟合阶数是一个参数变量,根据值的不同,存在欠拟合和过拟合的情况
1、使用到的包——MathNet
using MathNet.Numerics;
2、曲线拟合的函数
Fit.Polynomial(X, Y, k)
X和Y是一个同型的double数组
k是阶数,为int类型
3、一个简单地测试例子
double[] X = Enumerable.Range(1, 7).Select(r => (double)r).ToArray();
double[] Y = new double[] { 1, 3, 90, 150, 7, 6, 4 };
double[] parameters = Fit.Polynomial(X, Y, 5); //此处拟合阶数为5(阶数能取的最大值为:【样本个数 - 1】 = 6),此时返回的参数列表长度为【阶数+1】= 6
- 此处拟合阶数为5(阶数能取的最大值为:【样本个数 - 1】 = 6)
- 参数列表长度为【阶数+1】= 6
4、如何通过给定的x坐标值和拟合参数,计算y值
以上图为例,参数组合parameters计算出来为:[913.28 , -1786.49 , 1156.04 , -317.26 , 38.92 , -1.76]
简要记录为[p0,p1,p2,p3,p4,p5]
给定一个x值,要计算对应的y值,公式为
y = f(x) = p0 * x^0 + p1 * x^1 + p2 * x^2 + … + p5 * x^5
/// <summary>
/// 根据拟合参数和给定的x值,计算对应的y值
/// y = f(x) = p0 * x^0 + p1 * x^1 + p2 * x^2 + .... + pk * x^k
/// </summary>
/// <param name="X">x的坐标系列</param>
/// <param name="paras">拟合参数数组</param>
/// <returns>拟合出来的Y系列值</returns>
public double[] getNewY(double[]X,double[]paras)
{
var newY = X.Select(x =>
paras
.Select((p, index) => p * math.pow(x, index)) //计算多项式的每一项
.Sum() //所有项求和
).ToArray();
return newY;
}
5、原有样本太少,中间插入更多的估值点
- 【1】生成更密的x系列
/// <summary>
/// 在x1和x2之间插值,步进为step,生成一个新的系列[x1...x2]
/// </summary>
/// <param name="x1">起始值</param>
/// <param name="x2">结束值</param>
/// <param name="step">步进值</param>
/// <returns>返回的系列</returns>
public double[] genNewX(double x1, double x2, double step)
{
List<double> newX = new();
newX.Add(x1);
double currentX = x1;
while (currentX <= x2)
{
currentX += step;
newX.Add(currentX);
}
if (!newX.Contains(x2)) newX.Add(x2);
return newX.ToArray();
}
- 【2】计算x新列对应的y系列值
double[] parameters = Fit.Polynomial(X.ToArray(), Y.ToArray(), 5);
double[] newX = genNewX(X.Min(), X.Max(), 0.1f);
Debug.Log("生成新的X坐标完成");
//计算新的拟合值
var newY = getNewY(newX, parameters).ToList();
Debug.Log("生成新的Y坐标完成");
三、代码清单
using MathNet.Numerics;
using System;
using System.Collections.Generic;
using UnityEngine;
using XCharts.Runtime;
using System.Linq;
using Cysharp.Threading.Tasks;
using Unity.Mathematics;
/// <summary>
/// 曲线拟合
/// </summary>
public class FitPolynomial : MonoBehaviour
{
public GameObject charRoot;
public List<double> X = new List<double>();
public List<double> Y = new List<double>();
// Start is called before the first frame update
#if UNITY_EDITOR
[ContextMenu("曲线拟合")]
#endif
void FitPolynomialTest()
{
/*
* 多项式拟合如何计算?
*/
double[] X = Enumerable.Range(1, 7).Select(r => (double)r).ToArray();
double[] Y = new double[] { 1, 3, 90, 150, 7, 6, 4 };
double[] parameters = Fit.Polynomial(X, Y, 5); //阶数最大为【样本个数 - 1】
Debug.Log($"参数数组的大小为:{parameters.Length}");
//拟合参数的数组:数组大小为【阶数 + 1】,阶数最大只能为【样本个数 - 1】
parameters.ToList().ForEach(x => Debug.Log(x)); //显示参数
//计算结果值
List<double> result = new List<double>();
for (int i = 1; i < 8; i++)
{
result.Add(parameters[0] * math.pow(i, 0) + parameters[1] * math.pow(i, 1) + parameters[2] * math.pow(i, 2) + parameters[3] * math.pow(i, 3) + parameters[4] * math.pow(i, 4) + parameters[5] * math.pow(i, 5));
}
List<double> result2 = getNewY(X, parameters).ToList();
//Debug.Log($"Pow(2,0) = {math.pow(2,0)} \n Pow(2,1) = {math.pow(2, 1)} \n Pow(2,2) = {math.pow(2, 2)} ");
for (int i = 0; i < X.Length; i++)
{
Debug.Log($"{X[i]} {Y[i]} {result[i]} {result2[i]}");
}
}
/// <summary>
/// 根据拟合参数和给定的x值,计算对应的y值
/// y = f(x) = p0 * x^0 + p1 * x^1 + p2 * x^2 + .... + pk * x^k
/// </summary>
/// <param name="X">x的坐标系列</param>
/// <param name="paras">拟合参数数组</param>
/// <returns>拟合出来的Y系列值</returns>
public double[] getNewY(double[]X,double[]paras)
{
var newY = X.Select(x =>
paras
.Select((p, index) => p * math.pow(x, index)) //计算多项式的每一项
.Sum() //所有项求和
).ToArray();
return newY;
}
/// <summary>
/// 在x1和x2之间插值,步进为step,生成一个新的系列[x1...x2]
/// </summary>
/// <param name="x1">起始值</param>
/// <param name="x2">结束值</param>
/// <param name="step">步进值</param>
/// <returns>返回的系列</returns>
public double[] genNewX(double x1, double x2, double step)
{
List<double> newX = new();
newX.Add(x1);
double currentX = x1;
while (currentX <= x2)
{
currentX += step;
newX.Add(currentX);
}
if (!newX.Contains(x2)) newX.Add(x2);
return newX.ToArray();
}
#if UNITY_EDITOR
[ContextMenu("画散点图并拟合一条直线")]
#endif
void DrawLine()
{
Flow();
}
private async UniTask Flow()
{
//【1】=============画散点图=============
var scatter = charRoot.AddComponent<ScatterChart>();
scatter.Init();//初始化极为重要,不然在running状态会报空
var title = scatter.GetOrAddChartComponent<Title>();
title.text = "用给定的散点拟合出一条直线和一条曲线"; //主标题
await UniTask.Delay(TimeSpan.FromSeconds(2.0f));
scatter.SetSize(1024, 768);
scatter.AddSerie<Serie>("数据分布图");
Debug.Log($"数据长度为:{scatter.series[0].data.Count}"); //默认自带10个数据,需要删除
scatter.series[0].data.Clear();
await UniTask.Delay(TimeSpan.FromSeconds(2.0f));
var X = new List<double> { 1, 2, 3, 4, 5, 6,7,8 ,9,10,11,12,13};
var Y = new List<double> { -20, -8, 6, 48,200,300,500, 800,500,100, 20,2,0 };
var test = X.Zip(Y, (x, y) => new List<double> { x, y }).ToList();
X.Zip(Y, (x, y) => new List<double> { x, y }).ToList().ForEach(t =>
{
//Debug.Log($"添加数据:{t[0]} => {t[1]}");
scatter.AddData(0, t);
});
scatter.series[0].symbol.size = 9;//设置大小
//【2】=============直线拟合计算=============
await UniTask.Delay(TimeSpan.FromSeconds(2.0f));
var s = Fit.Line(X.ToArray(), Y.ToArray());
double b = s.Item1; //截距
double k = s.Item2; //斜率
//【3】=============画拟合出来的直线=============
var line1 = scatter.AddChartComponent<MarkLine>(); //添加一根直线
line1.data.Clear();//清空默认值,添加组的时候,会默认包含一个item
//增加一个端点数据
await UniTask.Delay(TimeSpan.FromSeconds(2.0f));
var p1 = new MarkLineData();
p1.type = MarkLineType.None;
p1.group = 1;
p1.xPosition = 0;
p1.yPosition = 0;
p1.xValue = X.Min();
p1.yValue = X.Min() * k + b;
p1.zeroPosition = false;
//标注【直线方程式】
await UniTask.Delay(TimeSpan.FromSeconds(2.0f));
var op = b > 0 ? "+" : "-";
var kStr = Math.Round(k, 2, MidpointRounding.AwayFromZero).ToString();
var bStr = Math.Round(math.abs(b), 2, MidpointRounding.AwayFromZero).ToString();
p1.name = $"y = {kStr} * x {op}{bStr}";
p1.label.formatter = "{b}";
//直线的形状设置
p1.lineStyle.type = LineStyle.Type.Solid;
p1.startSymbol.type = SymbolType.None;
p1.endSymbol.type = SymbolType.None;
//添加第二个端点数据
var p2 = new MarkLineData();
p2.type = MarkLineType.None;
p2.group = 1;
p2.xPosition = 0;
p2.yPosition = 0;
p2.xValue = X.Max();
p2.yValue = X.Max() * k + b;
p2.zeroPosition = false;
p2.name = $"y = {kStr} * x {op}{bStr}"; ;//"y = 0 * x + 15";
p2.label.formatter = "{b}";
Debug.Log($"y = {kStr} * x {op}{bStr}");
//直线的形状设置
p2.lineStyle.type = LineStyle.Type.Solid;
p2.startSymbol.type = SymbolType.None;
p2.endSymbol.type = SymbolType.None;
//端点数据加入直线中
line1.data.Add(p1);
line1.data.Add(p2);
//【4】曲线拟合:拟合参数的计算
double[] parameters = Fit.Polynomial(X.ToArray(), Y.ToArray(), 5);
double[] newX = genNewX(X.Min(), X.Max(), 0.1f);
Debug.Log("生成新的X坐标完成");
//计算新的拟合值
var newY = getNewY(newX, parameters).ToList();
Debug.Log("生成新的Y坐标完成");
//画拟合曲线
var serie2 = scatter.AddSerie<Line>("拟合曲线");
newX.Zip(newY, (x, y) => new List<double> { x, y }).ToList().ForEach(t =>
{
scatter.AddData(1, t);
});
scatter.RefreshAllComponent();
}
}