QGIS作为一个开源的非常好用的本地GIS工具,这里不在赘述,这里说它的一个比较有意思的内容。通过DEM数据展示3D地形。
-
下载DEM(高程数据)
比如从官网下载,或者从别的地方获取,这里就不在赘述。我这里下载使用的是一景:N26E101.hgt。
![]()
在QGIS中查看:

-
数据格式转换
通常我们做分析等都是使用的是Tif格式的文件,所以这里我使用GDAL命令行将其转换为tif,指定其投影是EPSG:4326。
gdalwarp -of GTiff -co COMPRESS=LZW -co BIGTIFF=YES -t_srs EPSG:4326 N26E101.hgt N26E101.tif
输出结果:

-
使用QGIS打开文件设置显示样式
(1)文件上右键点击,打开属性面板
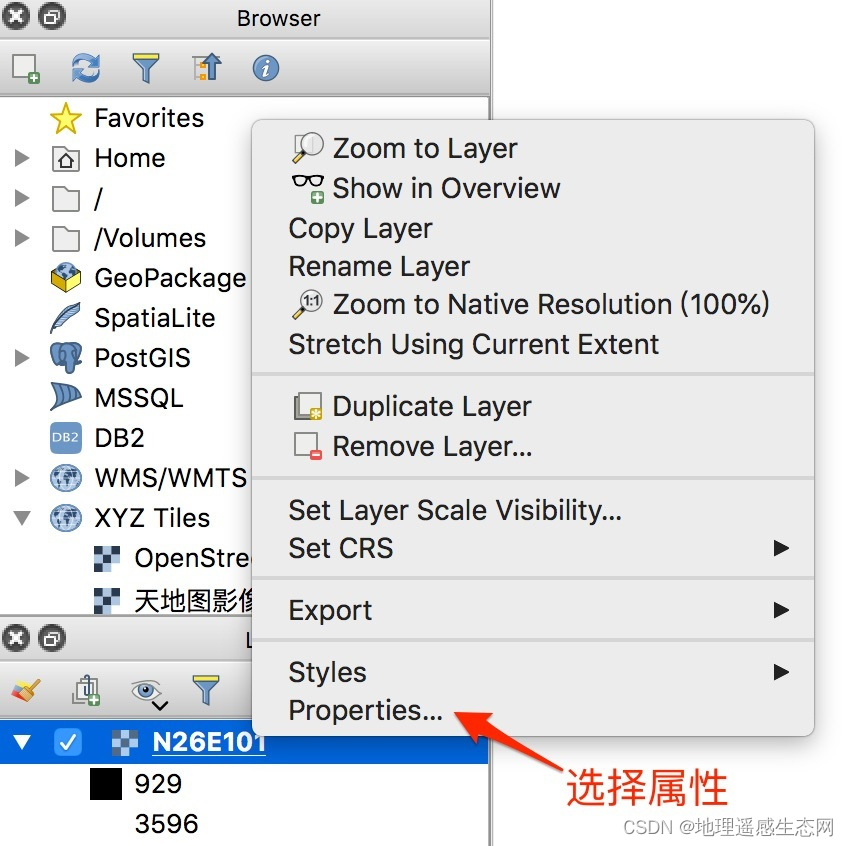
(2)设置渲染属性

渲染规则什么的填好后先点击Apply,然后点击 OK 确认。
(3)查看地图展示内容

-
点击QGIS中的新建3D Map View
(1)点击“View” -> “New 3D Map View”
(2)提示错误,我们需要重新制定投影信息。

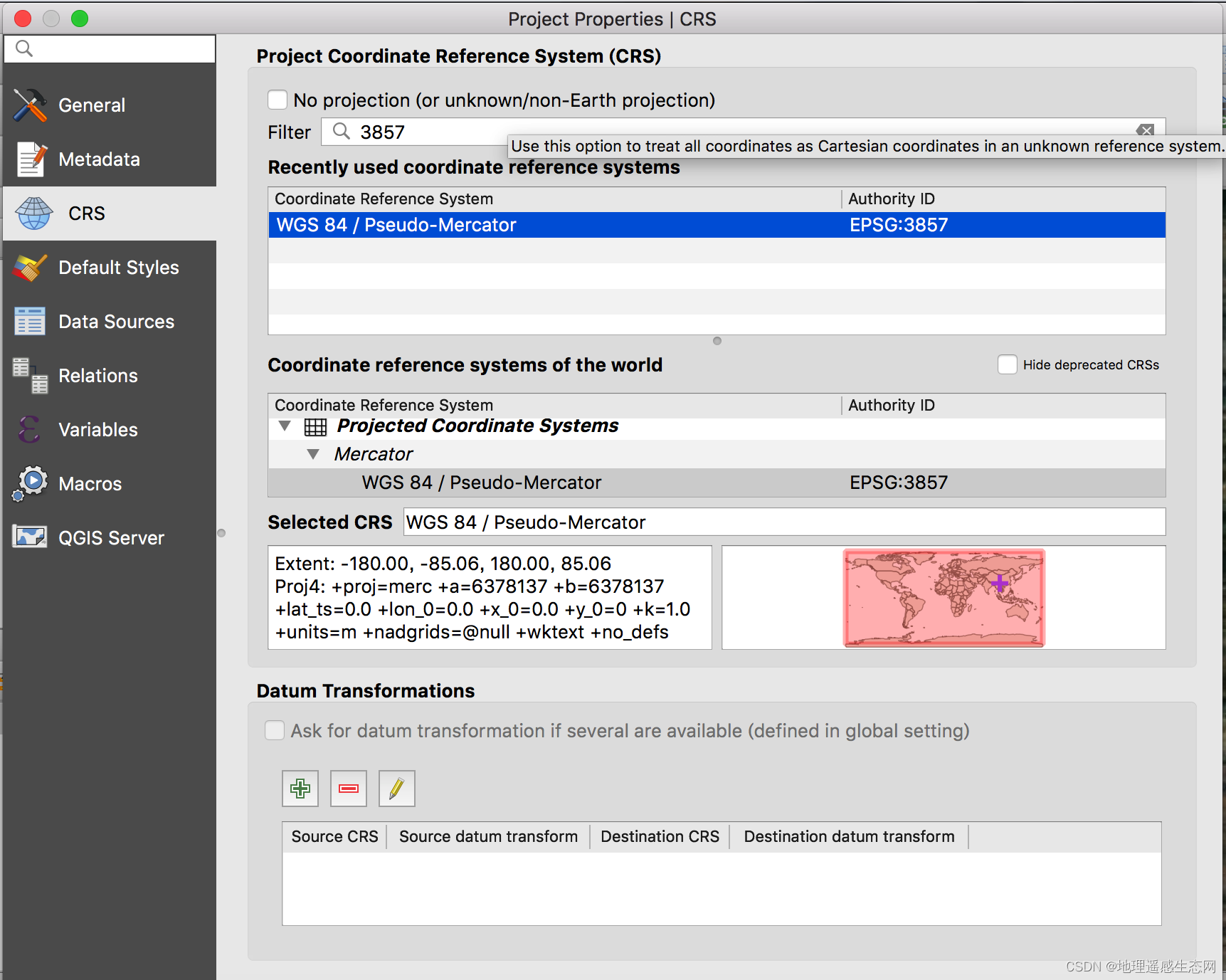
(3)修正投影信息
点击右下角

出现投影信息选择界面,这里我筛选EPSG:3857投影,然后选中投影信息在点击 apply,最后点击OK确认。
(4)重新新建3D Map View

-
设置3D Map的属性,显示3D的图像
(1)点击扳手出现属性设置界面,可以修改相关属性,修改完成后点击确认。
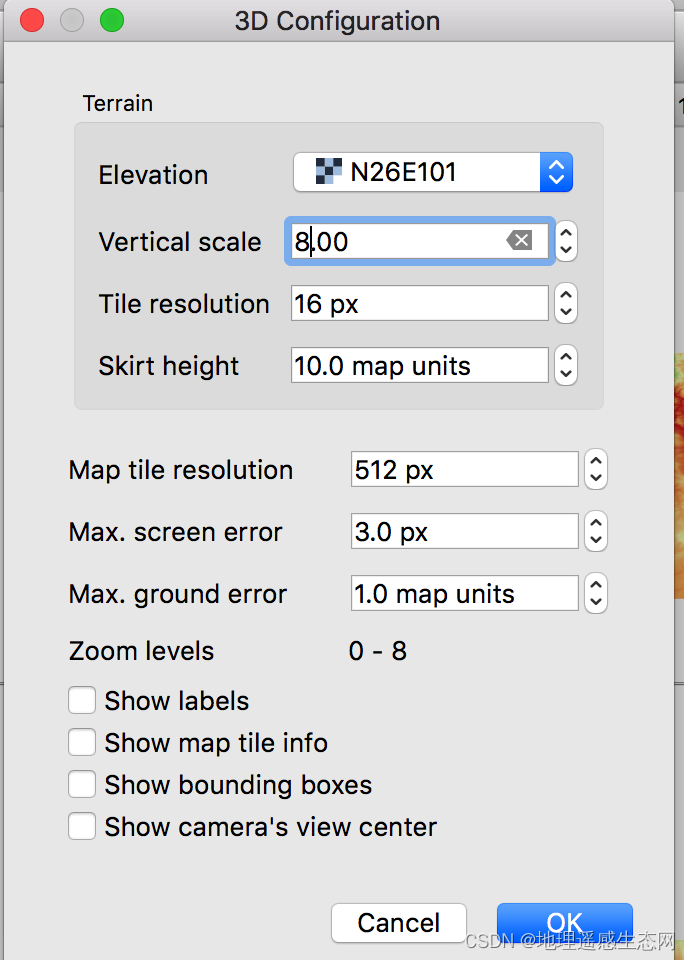
(2)设置属性后的图像

-
添加卫星影像,具体影像路径可以在网上查找

选择一张影像添加到QGIS图层中,如下图:
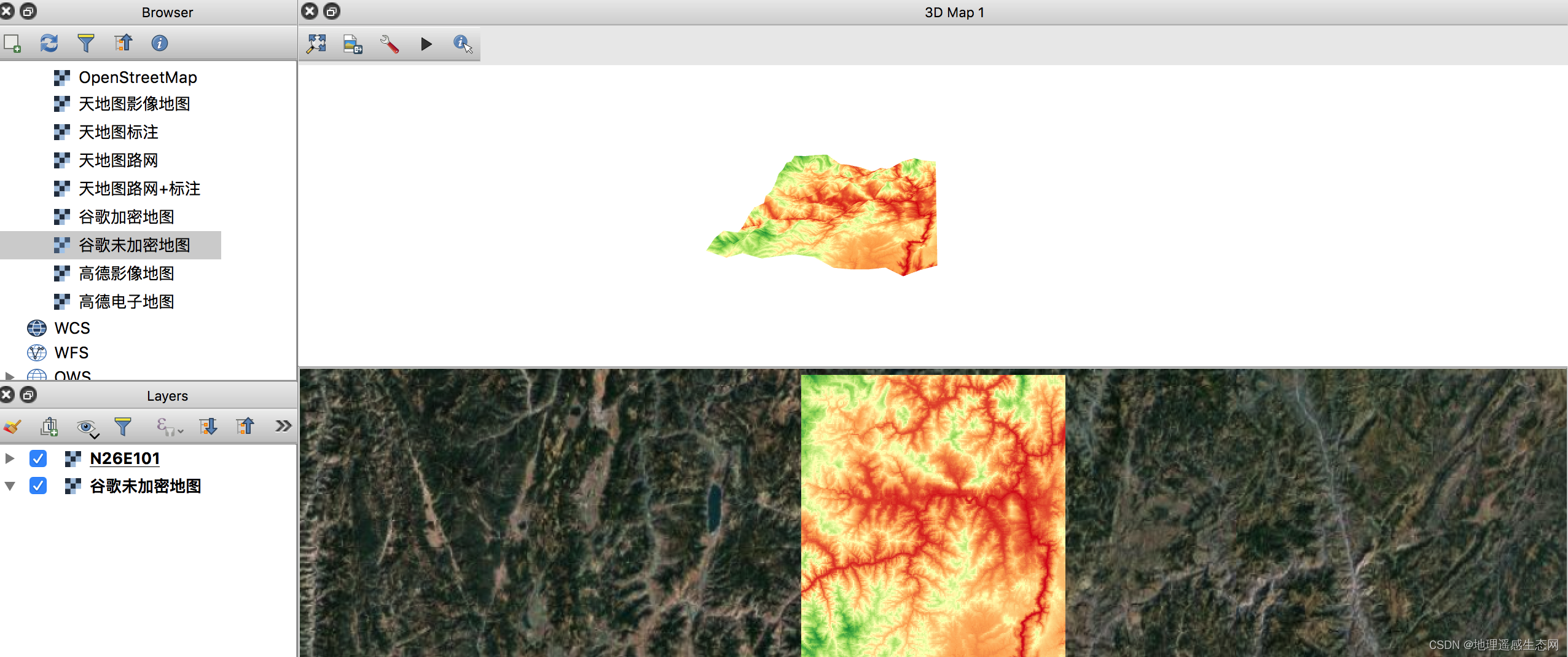
隐藏DEM图层

放大:

效果还可以。
来源请引用:地理遥感生态网科学数据注册与出版系统。