目录
- detrend函数去除基线
- 多项式拟合原函数
- BEADS 基线处理
- 小波算法
- 经验模态分解(EMD)
- 参考
detrend函数去除基线
detrend函数只能用于去除线性趋势,对于非线性的无能为力。
函数表达式:y = scipy.signal.detrend(x): 从信号中删除线性趋势:
x:含有基线干扰的信号;y:去除基线干扰后的信号。
detrend去基线代码显示:
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
t = np.linspace(0, 5, 100)
# normal是产生一个高斯分布
x = t + np.random.normal(size=100)
plt.subplot(2, 1, 1)
plt.plot(t, x, linewidth=3)
plt.subplot(2, 1, 2)
plt.plot(t, signal.detrend(x), linewidth=3)
plt.show()
结果展示:
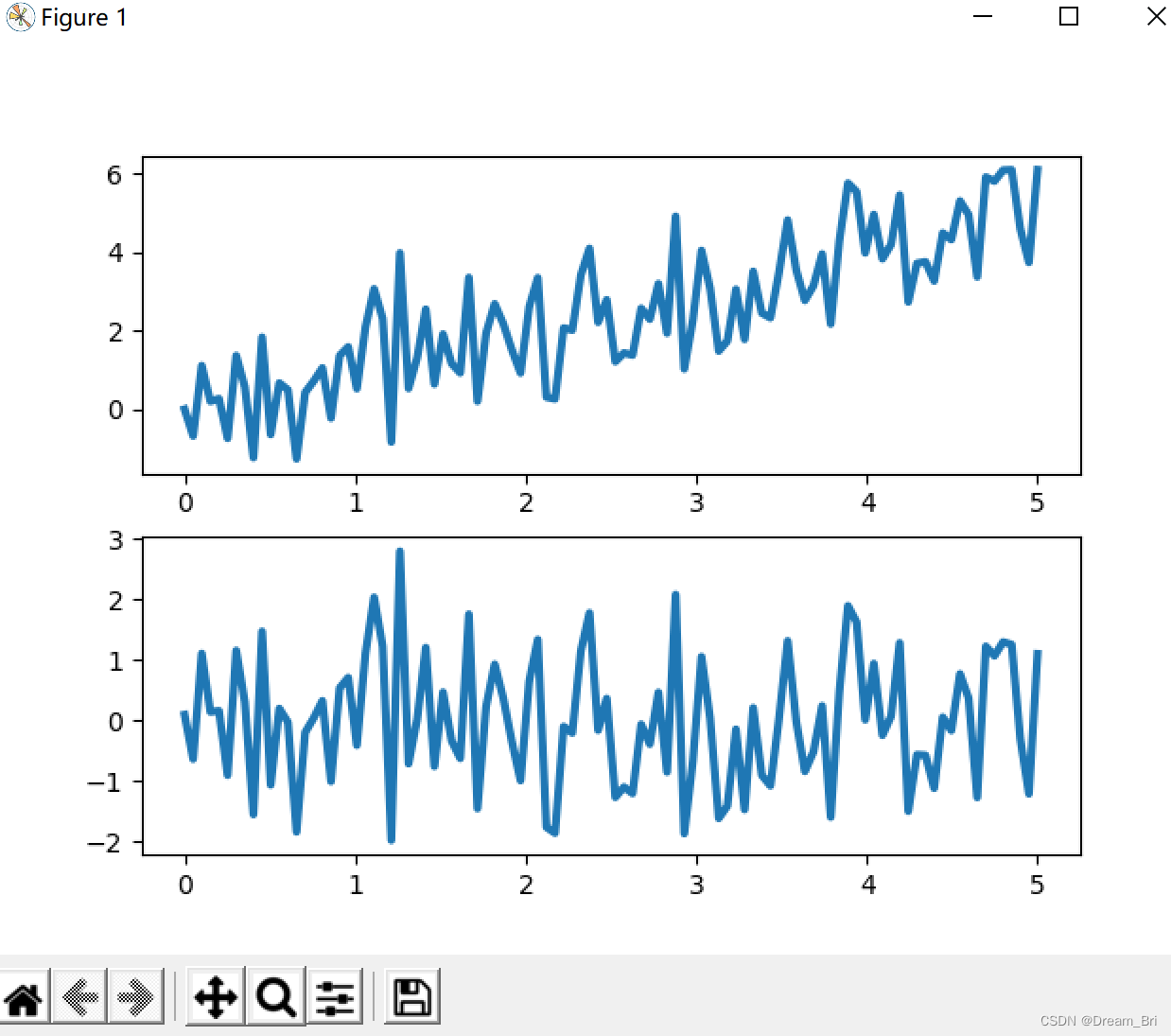
通过上图可以看到detrend去线性趋势效果很不错。
多项式拟合原函数
很容易理解,就是通过多项式拟合一个新的曲线,使拟合出来的曲线与原图像尽可能接近,同时又能去除图像中的噪声和基线等多余的因素。
代码显示为:
import os
import matplotlib.pyplot as plt
import scipy.signal
import numpy as np
def main():
# 项目目录
dir = "D:\\a_user_file\\8_data"
filename = 's1_run.csv'
path = os.path.join(dir, filename)
with open(path, "r") as fname:
data = fname.read()
lines = data.split("\n")
raw_data = []
for i in range(len(lines)):
line_i = lines[i].split(",")
raw_data.append(int(line_i[4]))
sig = raw_data
tmp_smooth1 = scipy.signal.savgol_filter(sig, 53, 9)
tmp_smooth2 = scipy.signal.savgol_filter(sig, 53, 3)
plt.subplot(3,1,1)
plt.plot(sig)
plt.subplot(3,1,2)
plt.plot(tmp_smooth1 * 0.5, label='mic'+ '拟合曲线-21', color='red')
plt.subplot(3,1,3)
plt.plot(tmp_smooth2 * 0.5, label='mic'+ '拟合曲线-53', color='green')
plt.show()
main()
显示结果如下:
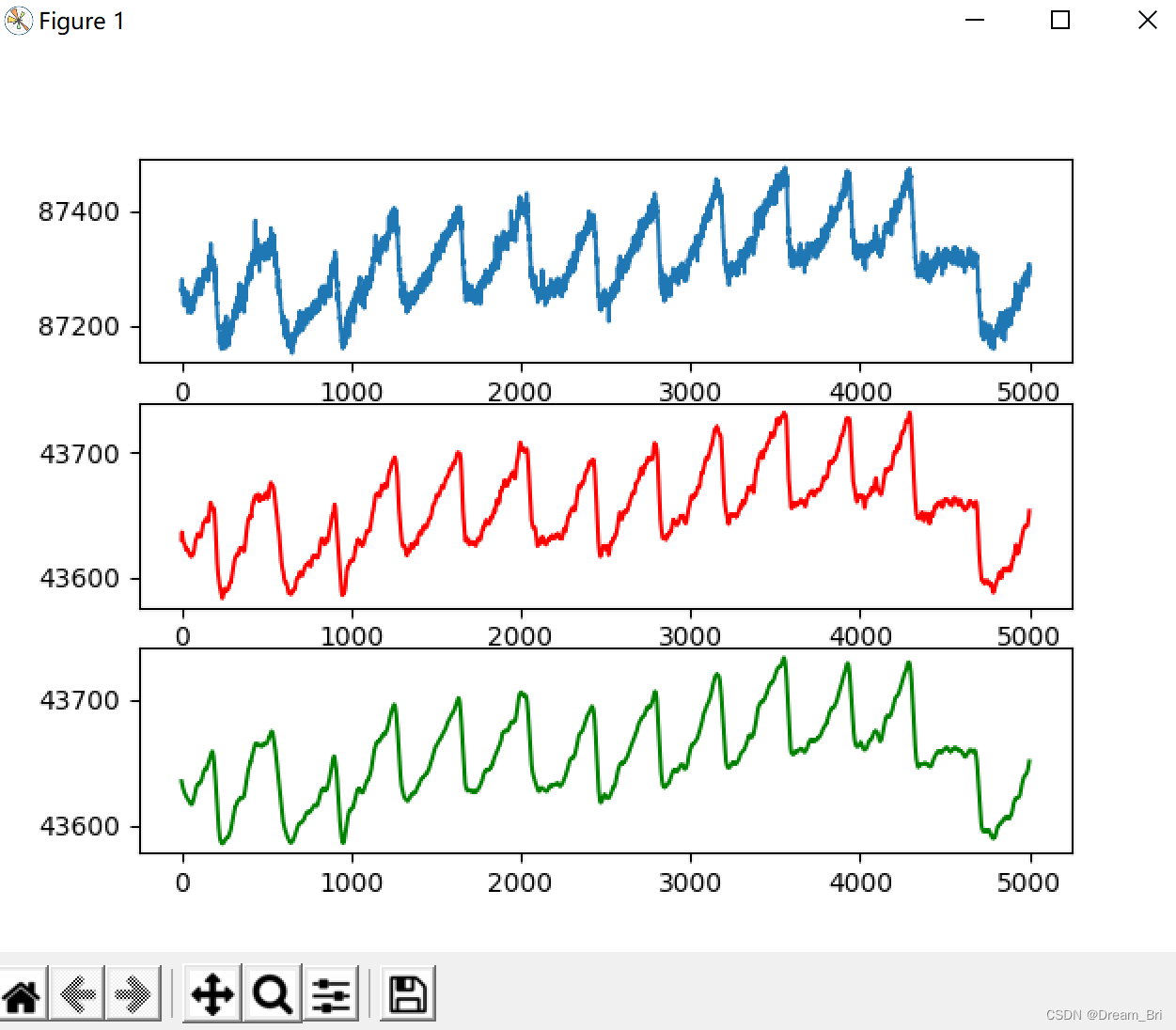
BEADS 基线处理
详细内容可参考:
https://ww2.mathworks.cn/matlabcentral/fileexchange/49974-beads-baseline-estimation-and-denoising-with-sparsity?s_tid=AO_FX_info
小波算法
小波算法去噪和去基线是先用滤波器对原始信号进行分解,经过下采样得到分解的高频系数D(细节部分)和低频系数A(近似部分),多层分解只需要对上一层分解出来的低频分量继续分解即可。这个过程就是小波分解。
从分解的最底层往上重构出信号,首先是上采样,一般采用隔值插零的方法,即增加数据量来达到与原始信号长度相同的数据,然后分别通过重构的高通滤波器g和低通滤波器h,最终重构出原始信号,如果代码编写的没问题,那么重构出的信号与原始信号完全一致。
而小波变换去噪的过程就是在分解后的各层系数中找出噪声所在的层,对该层的低频系数或者高频系数进行处理,比如软硬阈值处理,处理后再经过重构,即可重构出去除噪声的信号。
import numpy as np
import matplotlib.pyplot as plt
import pywt
import os
def signal():
# 项目目录
dir = "D:\\a_user_file\\8_data"
filename = '1.csv'
path = os.path.join(dir, filename)
with open(path, "r") as fname:
data = fname.read()
lines = data.split("\n")
raw_data = []
for i in range(len(lines)):
line_i = lines[i].split(",")
raw_data.append(int(line_i[0]))
return raw_data
data = signal()
x = range(0, len(data))
w = pywt.Wavelet('db8') # 选用Daubechies8小波
maxlev = pywt.dwt_max_level(len(data), w.dec_len)
print("maximum level is " + str(maxlev))
threshold = 0.5 # Threshold for filtering
# Decompose into wavelet components, to the level selected:
coeffs = pywt.wavedec(data, 'db8', level=maxlev) # 将信号进行小波分解
for i in range(1, len(coeffs)):
coeffs[i] = pywt.threshold(coeffs[i], threshold*max(coeffs[i])) # 将噪声滤波
datarec = pywt.waverec(coeffs, 'db8')
plt.subplot(2,1,1)
plt.plot(data, color="black", linewidth=2.0, linestyle="solid")
plt.subplot(2,1,2)
plt.plot(datarec, color="red", linewidth=2.0, linestyle="solid")
plt.show()
用小波变换去噪的关键是找到对应噪声、基线漂移所在的频率段,去掉对应的频率段,就可以生成新的去噪去基线信号了。
经验模态分解(EMD)
EMD方法认为任何信号都可以分解为若干个不同的本征模态函数,和一个残余量稳态量。其中各个本征模态函数反映了信号的局部特性,残余量反映了信号的趋势或均值。EMD法采用“筛”选的方法从原始信号中将残余量分离出来。
参考
https://ww2.mathworks.cn/matlabcentral/fileexchange/49974-beads-baseline-estimation-and-denoising-with-sparsity?s_tid=AO_FX_info
https://blog.csdn.net/qq_41620350/article/details/115981740
https://blog.csdn.net/u010565765/article/details/69397415