CNC三轴小线段路径规划
文章目录
- CNC三轴小线段路径规划
- 一、项目说明
- 二、具体实现
- 1、速度规划
- 2、小线段插补
- 3、运动学逆解刀轴插补点
- 4、差分处理得到实际的速度和加速度
- 5、加速度滑动平均
- 6、实现的效果如图所示
- 三、Reference
写在前面,本文是作为一个练手小项目的总结,方便以后自己查看,也欢迎大家批评指正。项目地址: GitHub
一、项目说明
参照论文《An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead 》给出的方法给五轴机床做速度规划。输入原始的刀心数据(x,y,z,i,j,k),对其进行速度规划和插补,获得插补后的数据(x,y,z,i,j,k),然后通过运动学逆解转化成刀轴数据(x,y,z,b,c)。通过差分计算实际的速度和加速度与规划的速度进行对比,最后观察平滑滤波后的实际加速度。
二、具体实现
1、速度规划
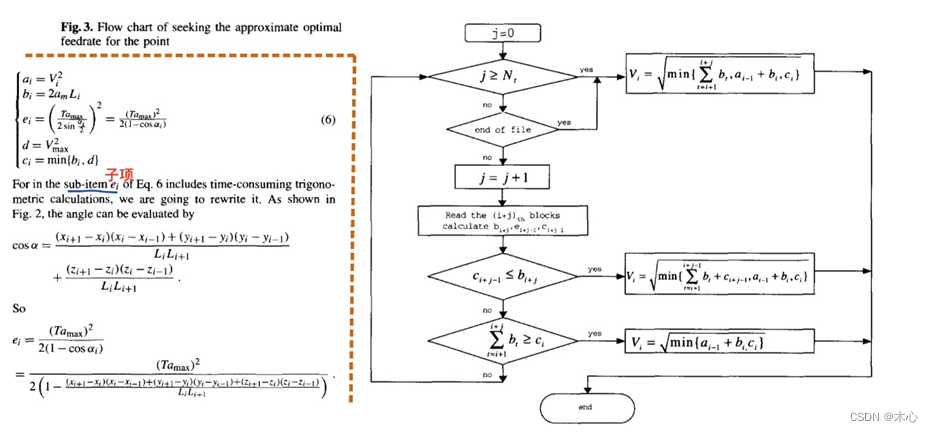
首先进行速度规划,按照如上的流程图(参考论文)对刀心的速度进行规划,计算得到每个刀心点对应的 ,具体的计算过程是先设定前瞻数,这里设定为4,然后通过判断上述循环条件,在

公式中选取对应的值作为当前的 ,具体的实现是代码中的speed_planning函数,函数的详细解释如下:
def speed_planning(traj_data, max_speed=MAX_SPEED, max_accel=MAX_ACCEL, corner_time=CORNER_TIME, period=PERIOD):
"""
:@func: 参考《An optimal feedrate model and solution algorithm for a
high-speed machine of small line blocks with look-ahead》给出的方法,进行速度规划
:param traj_data: 路径信息shape(num,3) (x,y,z)
:param max_speed=0.05: 最大合成速率 m/s
:param max_accel=0.5: 最大合成加速度 m/s^2
:param corner_time=0.003: 拐弯时间 s
:param period = 0.001: 插补周期 s
:return:
"""
# 定义常量
block_max = 4 # 最大前瞻数
num = len(traj_data)
# 开辟存储空间
a = np.zeros([num])
b = np.zeros([num])
e = np.zeros([num])
c = np.zeros([num])
d = np.power(max_speed,2)
Vs = np.zeros([num,1])
# 节点差分
dp = np.diff(traj_data, axis=0)
# 初始化
e[0] = d
b[0] = 0
b[1] = 2*max_accel*np.sqrt(np.power(dp[0],2).sum())
for i in range(1,num-1): # Vs中第一个速度和最后一个速度都为0
j = 0
if j < block_max:
if i+j <num:
j=j+1
b[i+j] = 2*max_accel*np.sqrt(np.power(dp,2).sum())
e[i+j-1] = corner_time*max_accel*max_accel / (2*(1-(dp[i+j-2,0]*dp[i+j-1,0]
+dp[i+j-2,1]*dp[i+j-1,1]
+dp[i+j-2,2]*dp[i+j-1,2])
/(np.sqrt(np.power(dp[i+j-2],2).sum())
*np.sqrt(np.power(dp[i+j-1],2).sum()))))
c[i+j-1] = np.min([e[i+j-1],d])
if c[i+j-1] > b[i+j]:
sum = 0
for k in range(i+1,i+j):
sum += b[k]
if sum >= c[i]:
Vs[i]=np.sqrt(np.min([Vs[i-1]*Vs[i-1]+b[i], e[i]]))
elif c[i+j-1] <= b[i+j]:
sum = 0
for k in range(i+1,i+j):
sum += b[k]
Vs[i] = np.sqrt(np.min([sum+c[i+j-1], Vs[i-1]*Vs[i-1]+b[i], e[i]]))
elif i+j >= num:
sum = 0
for k in range(i+1,i+j):
sum += b[k]
Vs[i] = np.sqrt(np.min([sum, Vs[i-1]*Vs[i-1]+b[i], e[i]]))
elif j>= block_max:
sum = 0
for k in range(i+1,i+j):
sum += b[k]
Vs[i] = np.sqrt(np.min([sum, Vs[i-1]*Vs[i-1]+b[i], e[i]]))
return Vs
2、小线段插补
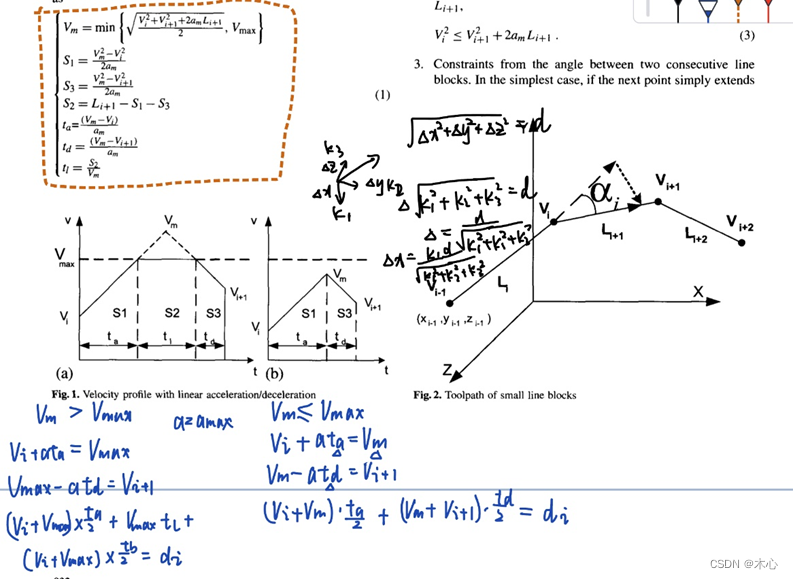
然后再按照上图的方法计算每一段插值时所需要的信息

具体实现函数是calc_lines_info
def calc_lines_info(path_data, plan_vels, max_speed=MAX_SPEED, max_accel=MAX_ACCEL):
"""
:@func: 三轴小线段计算中间信息函数
:param path_data: 初始路径信息 shape(n,6) (x,y,z,i,j,k)
:param plan_vels: 初始路径点的合成规划速度 shape(n,1)
:param max_speed = 0.05: 三轴最大合成速度 m/s
:param max_accel = 0.5: 三轴最大合成加速度 m/s^2
:return :
"""
num = path_data.shape[0]
# distances = np.zeros([num -1, 1]) #插值点间的距离shape(n-1, 3)
dp = np.diff(path_data[:,0:3],axis=0)
# 开辟存储空间
vels_m = np.zeros([num -1])
s1 = np.zeros([num -1])
s2 = np.zeros([num -1])
s3 = np.zeros([num -1])
ta = np.zeros([num -1])
td = np.zeros([num -1])
tl = np.zeros([num -1])
for i in range(num -1):
# 计算距离
# distances[i] = np.sqrt(np.power(path_data[i+1,0:3] - path_data[i,0:3],2).sum())
dis_i = np.sqrt(np.power(dp[i],2).sum())
# 计算合成速度
vi = plan_vels[i]
vi_1 = plan_vels[i+1]
# vels_m[i] = min(np.sqrt((np.power(vi,2) + np.power(vi_1,2) + 2*max_accel*distances[i])/2), max_speed)
vels_m[i] = min(np.sqrt((np.power(vi,2) + np.power(vi_1,2) + 2*max_accel*dis_i)/2), max_speed)
s1[i] = (np.power(vels_m[i],2) - np.power(vi,2))/2
s3[i] = (np.power(vels_m[i],2) - np.power(vi_1,2))/2
s2[i] = dis_i - s1[i] -s3[i]
ta[i] = (vels_m[i] - vi) / max_accel
td[i] = (vels_m[i] - vi_1) / max_accel
tl[i] = s2[i] / vels_m[i]
return vels_m, ta, td, tl
然后我们进行单条线段的插补,函数实现是calc_axis_point
def calc_axis_point(start, end, Vi, Vi_1, Vm, timea, timed, timel, max_accel=MAX_ACCEL, period=PERIOD):
"""
:@func: 计算一段的插补点
:param start: shape(6,)
:param end: shape(6,)
:param Vm: 该段的最大速度
:param Vi: 起始速度
:param Vi_1: 终点速度
:param timea: 加速时间
:param timed: 匀速时间
:param timel: 减速时间
:return: 返回给定两点之间的插补点,shape(n,6)
"""
dist = np.sqrt(np.power(end[0:3]-start[0:3],2).sum())
# 计算三轴x,y,z分别所占的比例
k1 = (end[0:3]-start[0:3])[0] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())
k2 = (end[0:3]-start[0:3])[1] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())
k3 = (end[0:3]-start[0:3])[2] / np.sqrt(np.power(end[0:3]-start[0:3],2).sum())
# 计算法向量的比例
delta = (end[3:]-start[3:]) / (timea+timed+timel)
# 插值周期数
t_count = 1
V1 = Vi #起始点速度
V2 = Vi_1 #终点速度
# 开辟存储空间
line_points = np.zeros([1,6])
dis = 0
while(t_count*period <= timea+timed+timel and dis<=dist):
# 计算加速时间内的插值点
if t_count*period <= timea:
dis += V1*period + 0.5*max_accel*period*period
V1 += max_accel*period
if V1 > Vm:
V1 = Vm
t_count += 1
delta_vec = delta * t_count * period
delta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)
dp = np.concatenate([delta_xyz, delta_vec], axis=0)
p = start + dp
line_points = np.vstack([line_points, p])
# 计算匀速时间内的插值点
elif timea < t_count*period <= timea+timel and timel!=0:
dis += V1 * period
t_count += 1
delta_vec = delta * t_count * period
delta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)
dp = np.concatenate([delta_xyz, delta_vec], axis=0)
p = start + dp
line_points = np.vstack([line_points, p])
# 计算减速时间内的插值点
elif timea+timel < t_count*period <= timea+timel+timed:
dis += V1*period - 0.5*max_accel*period*period
V1 = V1 - max_accel*period
if V1 < V2:
V1 = V2
t_count += 1
delta_vec = delta * t_count * period
delta_xyz = np.concatenate([k1*dis, k2*dis, k3*dis], axis=0)
dp = np.concatenate([delta_xyz, delta_vec], axis=0)
p = start + dp
line_points = np.vstack([line_points, p])
return line_points[1:]
再进行多条线段插补,函数实现是calc_axis_points
def calc_axis_points(path_data, plan_vels, max_speed=MAX_SPEED, max_accel=MAX_ACCEL, corner_time=CORNER_TIME, period=PERIOD):
"""
:@func: 计算所有的插补点
:param path_data: shape(num,6)
:param plan_vels: shape(num,)
:param max_speed = 0.05: 三轴最大合成速度 m/s
:param max_accel = 0.5: 三轴最大合成加速度 m/s^2
:param corner_time = 0.003: 拐弯时间 s
:param period = 0.001: 固定插补周期 s
:return: 所有的插补点,shape(n,6)
"""
vels_m, ta, td, tl = calc_lines_info(path_data, plan_vels, max_speed, max_accel)
# 开辟存储空间
axis_points = np.zeros([1,6])
num = len(path_data) - 1
for i in range(num):
line_points = calc_axis_point(path_data[i], path_data[i+1], plan_vels[i], plan_vels[i+1], vels_m[i], ta[i], td[i], tl[i], max_accel, period)
axis_points = np.vstack([axis_points, line_points])
return axis_points[1:]
3、运动学逆解刀轴插补点
然后使用运动学逆解,求出刀轴的坐标,函数实现是inv_kinema
def inv_kinema(path_data):
"""
:@func: 求解逆运动学
:param path_data: 刀心路径点信息 shape(num,6) (x,y,z,i,j,k)
:return : 求解的刀轴信息 shape(num,5) (x,y,z,b,c)
"""
#加载数据
points = read_path_data(DATA_PATH)
curve_points = points[:,0:3] # 路径
normal_vectors = points[:,3:] # 法向量
# 旋转轴初始方向
wc = sympy.Matrix([[0], [0], [1]])
wb = sympy.Matrix([[0], [0.5 * sympy.sqrt(2)], [0.5 * sympy.sqrt(2)]])
theta_b, theta_c ,x,y,z= sympy.symbols('theta_b theta_c x y z')
# 对C旋转
cRodrigues = Rodrigues(wc, theta_c)
# 对B旋转
bRodrigues = Rodrigues(wb, theta_b)
# print(bRodrigues)
zero=np.zeros((3,1))
# 生成旋转矩阵
ec=np.append(cRodrigues,zero,axis=1)
e_bu=np.array([0,0,0,1]).reshape(1,4)
e_c=np.append(ec,e_bu,axis=0).reshape(4,4)
eb=np.append(bRodrigues,zero,axis=1)
e_b=np.append(eb,e_bu,axis=0).reshape(4,4)
# print(eb,e_b)
e_x=np.array([1,0,0,x,0,1,0,0,0,0,1,0,0,0,0,1]).reshape(4,4)
e_y=np.array([1,0,0,0,0,1,0,y,0,0,1,0,0,0,0,1]).reshape(4,4)
e_z=np.array([1,0,0,0,0,1,0,0,0,0,1,z,0,0,0,1]).reshape(4,4)
# 初始位型
mt0 = np.array([1,0,0,10,0,1,0,20,0,0,1,100,0,0,0,1]).reshape(4,4)
gmw=np.eye(4)
gmt1=np.dot(e_x,e_y)
gmt2= np.dot(gmt1,e_z)
gmt3=np.dot(e_c,e_b)
gmt4=np.dot(gmt3,mt0)
gmt=np.dot(gmt2,gmt4)
# 转移矩阵
gm=np.dot(gmw,gmt)
# 带入解析式,求解
bx = normal_vectors[:,0]/np.linalg.norm(normal_vectors[:,0])#归一化
by = normal_vectors[:,1]/np.linalg.norm(normal_vectors[:,1])
bz = normal_vectors[:,2]/np.linalg.norm(normal_vectors[:,2])
x = curve_points[:,0]
y = curve_points[:,1]
z = curve_points[:,2]
print(2*bz-1)
theta_b = np.arccos(2*bz-1)
theta_c = np.arcsin(((bz-1)*bx+np.sqrt(2)*np.sqrt(bz-bz**2)*by)/(1-bz**2))
# 存数据
myfile = open("path_interpolation_xyzbc.txt", "w")
myfile.write('x y z b c\n')
for i in range(0, normal_vectors.__len__()):
myfile.write('{:>6.3f} '.format(x[i]))
myfile.write('{:>6.3f} '.format(y[i]))
myfile.write('{:>6.3f} '.format(z[i]))
myfile.write('{:>6.3f} '.format(theta_b[i]))
myfile.write('{:>6.3f}\n'.format(theta_c[i]))
myfile.close()
4、差分处理得到实际的速度和加速度
接着用速度差分查看实际的速度,函数实现是diff_vel_accel
def diff_vel_accel(axis_points, period=PERIOD):
"""
:@func: 通过五轴插补点计算实际速度和实际加速度
:param axis_points: 实际插补点
:param period: 插补周期
:return: 实际速度, 实际加速度
"""
delta_d = np.diff(axis_points[:,0:3], axis=0)
dv = delta_d / period
real_vels = np.sqrt(np.power(dv,2).sum(axis=1))
delta_v = np.diff(dv, axis=0)
da = delta_v / period
real_accels = np.sqrt(np.power(da,2).sum(axis=1))
# print(real_vels[0:5])
# print(real_accels[0:5])
# 将实际速度写入到文件real_velocities.txt中
write2file('real_velocities.txt', real_vels, string = "real velocities")
# 将实际加速度写入到文件real_accelerations.txt中
write2file('real_accelerations.txt', real_accels, string="real accelerations")
return real_vels, real_accels
5、加速度滑动平均
最后对实际的加速度进行滑动平均,与设定值进行比较,函数实现是sliding_average
def sliding_average(data, window_size):
"""
:@func: 实现滑动平均滤波
:param data: 滑动滤波的数据
:param window_size: 滑动窗口大小
"""
filtered_data = []
for i in range(len(data)):
if i < window_size:
filtered_data.append(sum(data[:i+1]) / (i+1))
else:
filtered_data.append(sum(data[i-window_size+1:i+1]) / window_size)
write2file("filtered_accelerations.txt", filtered_data, string = "filtered accelerations")
return filtered_data
6、实现的效果如图所示
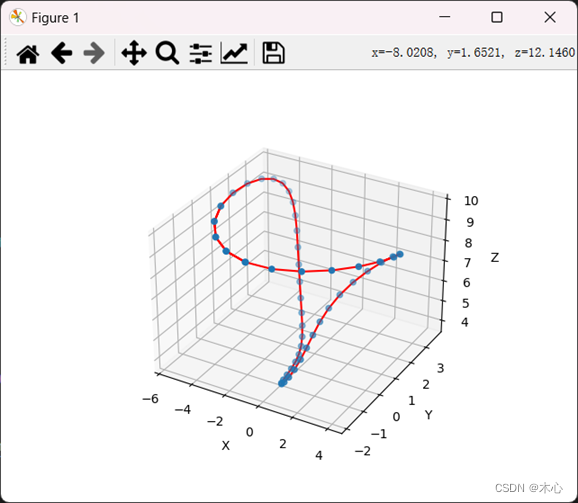
其中,蓝色的点是原始路径点,红色的线是由插补点绘制的小线段轨迹。
三、Reference
1、《An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead 》








![[HarekazeCTF2019]Easy Notes](https://img-blog.csdnimg.cn/88656c0b54b943c6b24a99e40e33ba17.png)