随机游走

基本思想
从一个或一系列顶点开始遍历一张图。在任意一个顶点，遍历者将以概率1-a游走到这个顶点的邻居顶点，以概率a随机跳跃到图中的任何一个顶点，称a为跳转发生概率，每次游走后得出一个概率分布，该概率分布刻画了图中每一个顶点被访问到的概率。用这个概率分布作为下一次游走的输入并反复迭代这一过程。当满足一定前提条件时，这个概率分布会趋于收敛。收敛后，即可以得到一个平稳的概率分布。

最经典的一维随机游走问题有赌徒输光问题和酒鬼失足问题。

（1）赌徒在赌场赌博，赢的概率是p，输的概率1-p，每次的赌注为1元，假设赌徒最开始时有赌金1元，赢了赌金加1元，输了赌金减1元。问赌徒输光的概率是多少？
（2）一个醉鬼行走在一头是悬崖的道路上，酒鬼从距离悬崖仅一步之遥的位置出发，向前一步或向后退一步的概率皆为1/2，问酒鬼失足掉入悬崖的概率是多少？

图的随机游走

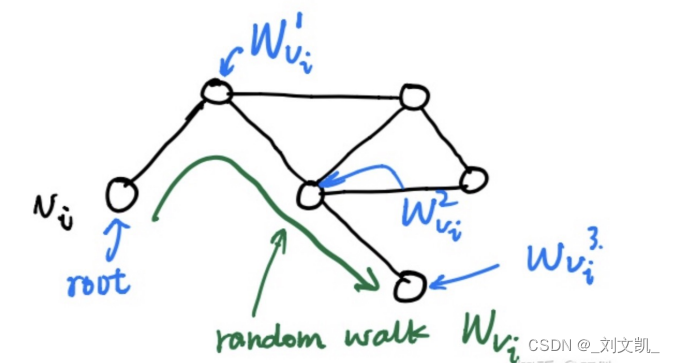
上图中的random walk 就是形成了一条随机游走链（N1,N2,N3,N4)，其中N1的又有本身的编码，N1=(a1, a2, a3)，即一个3维的embedding.

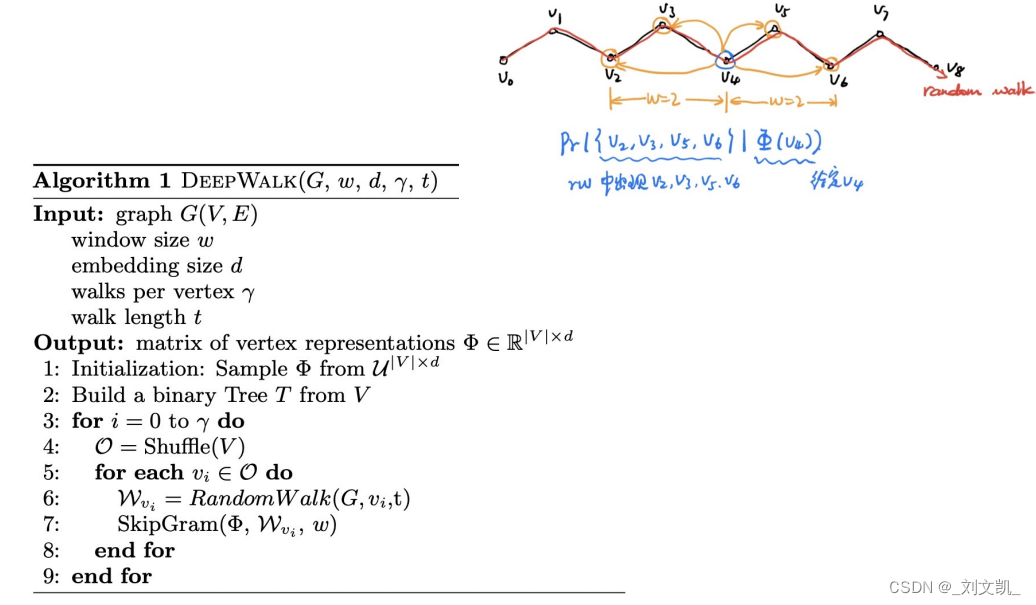
在上图中发Φ表示embedding， |V|xd即v个节点乘以d维编码，例如，上文提到的N1节点 N1=(a1, a2, a3)就是3维编码。

SkipGram
SkipGram就是给定一个中心词，去预测它的上下文
假设在我们的文本序列中有5个词，[“the”，“man”，“loves”，“his”，“son”]。

假设我们的窗口大小skip-window=2，中心词为“loves”，那么上下文的词即为：“the”、“man”、“his”、“son”。这里的上下文词又被称作“背景词”，对应的窗口称作“背景窗口”。

跳字模型能帮我们做的就是，通过中心词（target word）“loves”，生成与它距离不超过2的背景词（context）“the”、“man”、“his”、“son”的条件概率，用公式表示即：

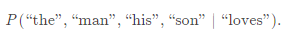
进一步，假设给定中心词的情况下，背景词之间是相互独立的，公式可以进一步得到

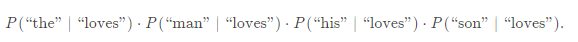
用概率图表示为：

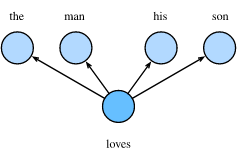
可以看得出来，这里是一个一对多的情景，根据一个词来推测2m个词，（m表示背景窗口的大小），上图窗口大小为2.