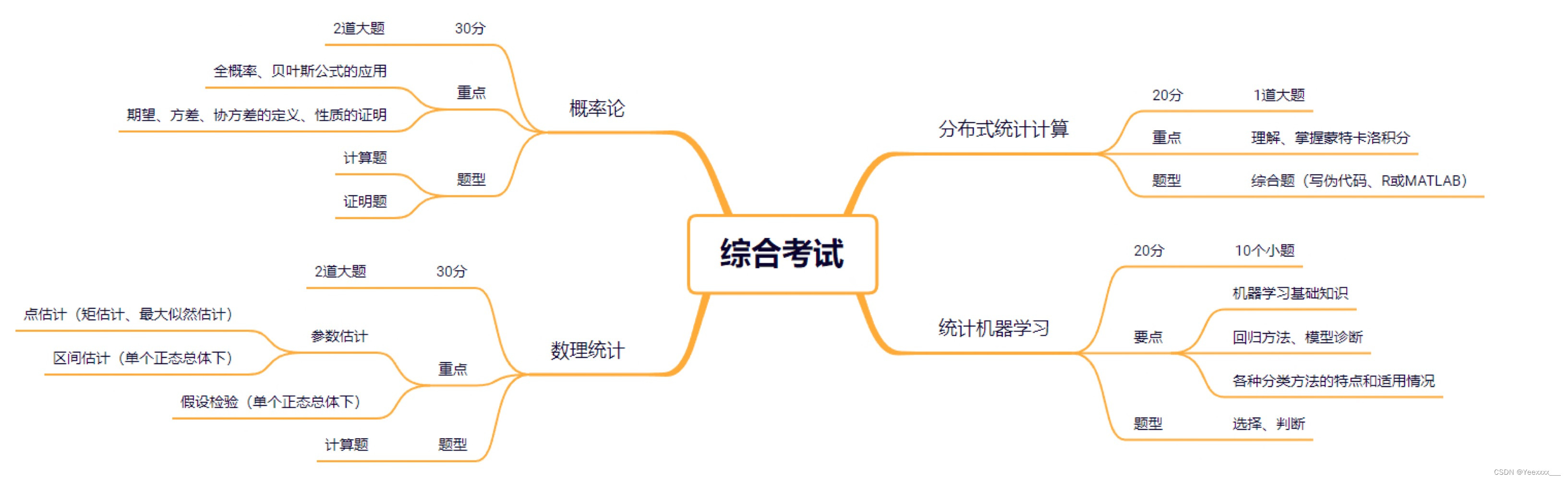
- 一、概率论
- 1、全概率公式、贝叶斯公式应用
- 2、期望、方差、协方差的定义以及性质证明
- (1) 期望
- (2) 方差
- (3) 协方差
- 二、数理统计
- 1、参数估计
- (1) 矩估计
- (2) 最大似然估计
- (3) 综合例题
一、概率论
1、全概率公式、贝叶斯公式应用

记住标黄的两段,上考场直接套数据,公式都不用写

2、期望、方差、协方差的定义以及性质证明
(1) 期望

(2) 方差
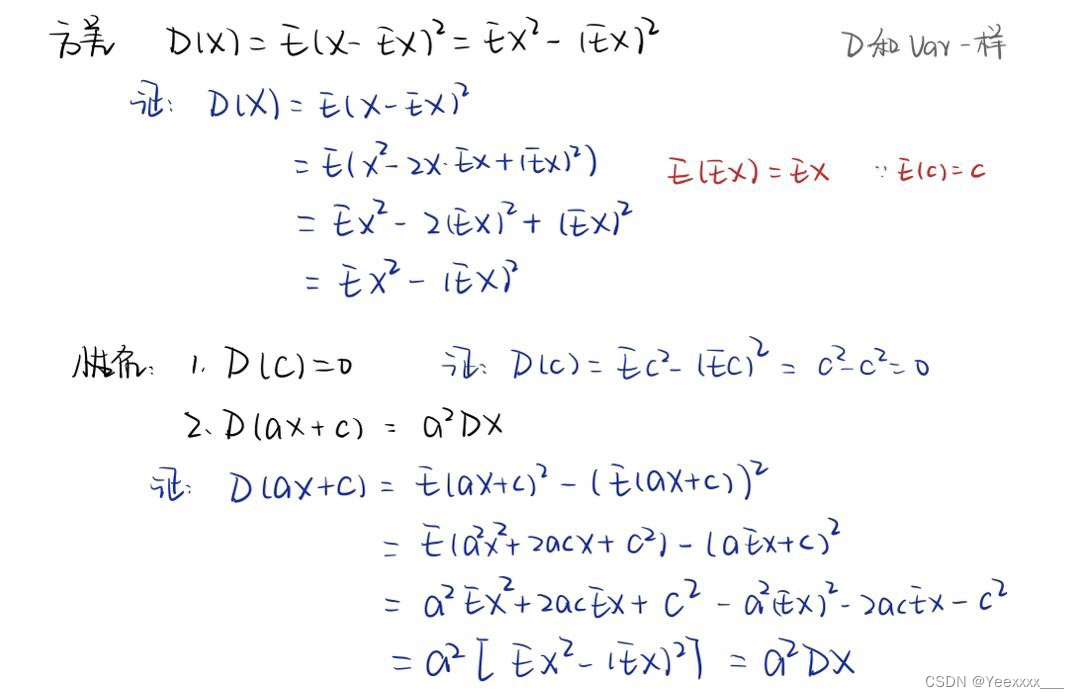
(3) 协方差

二、数理统计
1、参数估计
(1) 矩估计
令总体期望等于样本均值 ,即
E
X
=
X
‾
EX=\overline{X}
EX=X
(2) 最大似然估计
定义:使似然函数取得最大值的
θ
\theta
θ
三步走:
① 写出似然函数
L
(
θ
)
L(\theta)
L(θ),即概率密度的乘积;
② 取对数,求导数;
③ 令导数为0,得
θ
\theta
θ的最大似然估计量。
极大似然估计的特殊情况,即
L
(
θ
)
L(\theta)
L(θ)去除所有常数后,剩余与
θ
\theta
θ 有关的部分是个幂函数,取对数、求导数后的结果应大于0,此时需要用极大似然估计的定义求解。具体分析可见综合例题第三小问。
(3) 综合例题