Image super-resolution with an enhanced group convolutional neural network

（基于增强型分组卷积神经网络的图像超分辨率）

具有较强学习能力的神经网络被广泛应用于超分辨率问题的求解。然而，CNNs依赖于更深层次的网络结构来提高图像超分辨率的性能，这通常会增加计算成本。本文提出了一种浅层结构的增强型超分辨率神经网络（ESRGCNN），充分融合深宽通道特征，利用单幅图像超分辨率（SISR）中不同通道间的相关性提取更准确的低频信息。此外，ESRGCNN中的信号增强操作对于继承更多的远距离上下文信息以解决长期依赖性是有用的。将自适应上采样操作汇聚到CNN中，得到不同尺寸低分辨率图像的图像超分辨率模型。

介绍

图像超分辨率（SR）技术致力于通过经典方程y = x_↓s从不清晰的观测中恢复出更清晰的图像，其中x是高清晰度（也称为高分辨率，HR）图像，y表示不清晰（也称为低分辨率，LR）图像，s表示给定的比例因子。具体地，根据上述等式，可以通过下采样操作从多个HR图像获得相同的LR图像。即SISR问题不存在唯一解，可称为不适定反问题。为了解决这一问题，学者们提出了许多单幅图像随机共振（SISR）方法。例如，Hong等人将LR-HR对的斑块划分为不同的聚类，然后根据这些聚类在图像超分辨率中制定模糊规则。Liu等人改进了图像超分辨率中带旋转的加权随机森林模型。图像超分辨率方法中有一些比较有效的方法，基于插值的技术、基于稀疏的字典学习技术、近邻嵌入技术和贝叶斯技术。虽然这些方法都获得了优异的图像超分辨率性能，但其中一些方法可能会丢失细节信息，从而限制了SISR性能的效果。而且，由于手动调谐，这些方法中的大多数不灵活。此外，它们通常依赖于复杂的优化算法来提高SISR的性能，这将降低SISR的效率。
近来，由于插件式网络架构和灵活的训练机制，深度网络具有强大的自学习能力，从而获得更好的恢复性能。例如，Cui等人在图像超分辨率中使用了具有非局部自相似性的多个堆叠自动编码器。Dong等人提出了一种称为SRCNN的3层CNN模型，通过像素映射策略恢复高质量图像。SRCNN虽然比传统超分辨率方法获得了更有效的超分辨率结果，但收敛速度慢，训练代价大。为了克服这一问题，设计了更深层次的网络架构以追求优异的SR效果。例如，Kim等人通过堆叠一系列卷积层、残差学习（RL）技术和梯度裁剪操作来加速SR模型的训练，设计了更深层次的网络架构VDSR。因斯，通过多次使用RL技术来增强来自不同层的本地信息的效果成为流行，以进一步减轻训练难度并提升SR性能。深度递归残差网络（DRRN）融合了RL和递归学习策略，以提高SR方法的泛化能力。具体而言，RL技术可以降低SR模型的训练难度，递归学习技术可以在网络深度和参数之间进行权衡。或者，残差编码器-解码器网络（RED）通过利用RL技术连接卷积和去卷积层，以构建用于预测HR图像的对称CNN。此外，更深记忆网络（MemNet）使用RL技术挖掘不同层次的特征，以增强SISR中前一层的影响。使用信号处理思想（即，小波变换）转换为CNN可以实现SISR的突出性能。深度CNN和小波思想的结合可以获得更详细的信息，以提高预测图像的质量。虽然这些方法可以恢复高清晰度图像，但是它们使用双三次运算来构造SR网络的输入，从而具有高计算成本。为了克服上述缺点，学者们直接使用LR图像作为SR网络的输入来预测从给定的不清晰图像到高清晰图像的关系。Dong，Loy，and Tang等人率先使用上采样操作来放大所获得的低频特征的分辨率，这可以在降低视觉效果的同时加快训练速度。
充分利用不同网络层的层次特征，增强低频特征的鲁棒性，提高预测SR图像的分辨率。例如，Lim等人提出了一种增强型深度网络，称为增强型深度SR网络（EDSR），通过利用多尺度技术融合不同的低频特征来改善视觉效果。此外，Zhang等人利用不同的过滤器大小来挖掘不同的特征，然后融合这些特征以生成SR中更准确的特征。虽然这些方法取得了很好的SR结果，但是它们的更深层次的网络结构遭受了更大的计算代价。此外，这些随机共振模型只能通过一个模型处理单个尺度，不能满足真实的应用的需要。本文提出了一种增强型超分辨率分组CNN（ESRGCNN），主要通过堆叠6个分组增强卷积块（GEB），将卷积和激活函数的组合、自适应上采样机制和单个卷积层连接起来。具体地，GEB使用群卷积和RL技术来增强所获得的低频信息在不同信道的相关性方面的表达能力，以平衡SISR性能和复杂度。此外，该组合可以防止所获得的低频信息的过度增强。GEB中的信号增强操作可以通过跳跃连接操作从浅层继承长距离上下文信息，为深层提供补充信息，这有助于处理长期依赖能力。同时，利用自适应上采样机制，得到不同尺度下LR频率特征到HR频率特征的超分辨率特征映射，满足了SR技术对数字设备的要求。另外，最终卷积层用于构造HR图像。

贡献

1）提出的40层ESRGCNN利用群卷积和残差运算来增强不同信道的深度和广度相关性，从而实现高效的SR网络。
2）采用自适应上采样机制得到灵活的随机共振模型，有利于真实的应用。
3）Shallow ESRGCNN仅使用了134层RDN的5.6%和384层CSFM的9.6%的参数就获得了良好的视觉效果，在恢复1024 × 1024的HR图像时，其运行时间仅为常用RDN和CSFM的3%。

相关工作

Deep CNNs based group convolutions for SISR

许多深刻的学习方法有较强的自主学习能力被用于SISR。因为大多数的这些方法都是平等对待跨渠道加强SISR分层特性的影响，阻碍了表达能力的CNN。为了解决这个问题，SISR中发展了基于深CNN的群卷积。大致包括两种类型，如基于关注渠道和特征融合的通道。
第一类是利用注意技术强化关键通道的作用，提高SISR的性能和速度。例如，Hu等人将通道注意力和空间注意力合并到更深的网络中，以提取显著的低频信息，从而提高SISR性能。此外，Dai等人利用二阶特征统计量来获得SISR的更准确特征和更具区分性的表示。
第二类通过RL或级联操作融合分层信道特征，为SISR提供丰富的低频信息。例如，Jain等人通过群卷积去除无用连接，以加快SR模型的训练速度。此后，为了获得更稳健的特征，Zhao等人依靠两个基于信道的子网络来扩展多样性，以在SISR中提供互补特征。为了进一步降低SR模型的复杂性，提出了通过组卷积的基于特征融合的通道。例如，Yang等人利用softmax特征融合机制和spindle块来减少用于构建轻量级盲SR网络的参数。或者，级联具有多个卷积的多个群卷积网络可以降低SR网络的复杂度。为了解决复杂场景，多模态深度学习技术将同一场景的多模态图像使用到两个子网络中以提取互补特征，从而提高图像处理任务的性能。此外，为了提取谱特征的序列属性，提出了一种基于变换的序列透视图来学习谱局部序列信息。而且，跨层跳跃连接用于增强所设计的网络的存储能力，以提高图像分类的性能。以上两种方法对图像超分辨率的实现具有重要的参考价值。
所有这些方法都说明了SISR算法在性能和复杂度方面的有效性。因此，本文将群卷积用于SISR。与其他分组卷积随机共振方法不同，该方法通过相邻两层增强不同信道的相关性，而不是将当前层作为后续层的输入，从而提取出更准确的低频特征，降低了SISR的复杂度。

Multilevel feature fusion for SISR

根据前面的说明，已知单个特征学习方法不能保证复杂屏幕的学习特征的鲁棒性。受此启发，开发了特征融合方法。由于其良好的性能，该方法在高级计算机视觉任务中很受欢迎。此外，已知具有大深度的网络可能保持较浅层的较差记忆能力。为了克服这一挑战，提出了CNNs中的多级特征融合方法，以扩大局部特征对SR任务的影响。一般包括两种：低频特征融合和高频特征融合。
第一类采用双三次插值方法放大LR图像作为深层网络的输入，充分利用层次高频特征得到SR模型。例如，深度递归卷积网络（DRCN）结合了递归监督和跳跃连接操作，以增强所获得的分层信息的效果，从而减轻训练难度。此外，MemNet利用递归单元和门单元来增强当前层的能力，以提高SISR中深度网络的表达能力。这些方法虽然能获得高质量的图像，但复杂度较高。
第二类直接利用LR图像作为深度网络的输入，充分利用层次低频特征，以较快的处理速度获得更准确的信息。最后，该方法利用网络深层的上采样操作，将获得的信息放大，构造出HR图像。级联残差网络（cascading residual network，CRAN）利用级联分块和RL运算来增强局部特征，以提取SISR中更丰富的信息。或者，增强SR CNN（LESRCNN）将RL技术融合到异构卷积结构中，以从深层增强低频特征，从而实现显著的SR性能和快速。
通过以上的研究，可以看出多级特征融合方法可以有效地获得更清晰的图像。由于第一类方法复杂度较高，本文采用第二类方法的思想，如图1所示。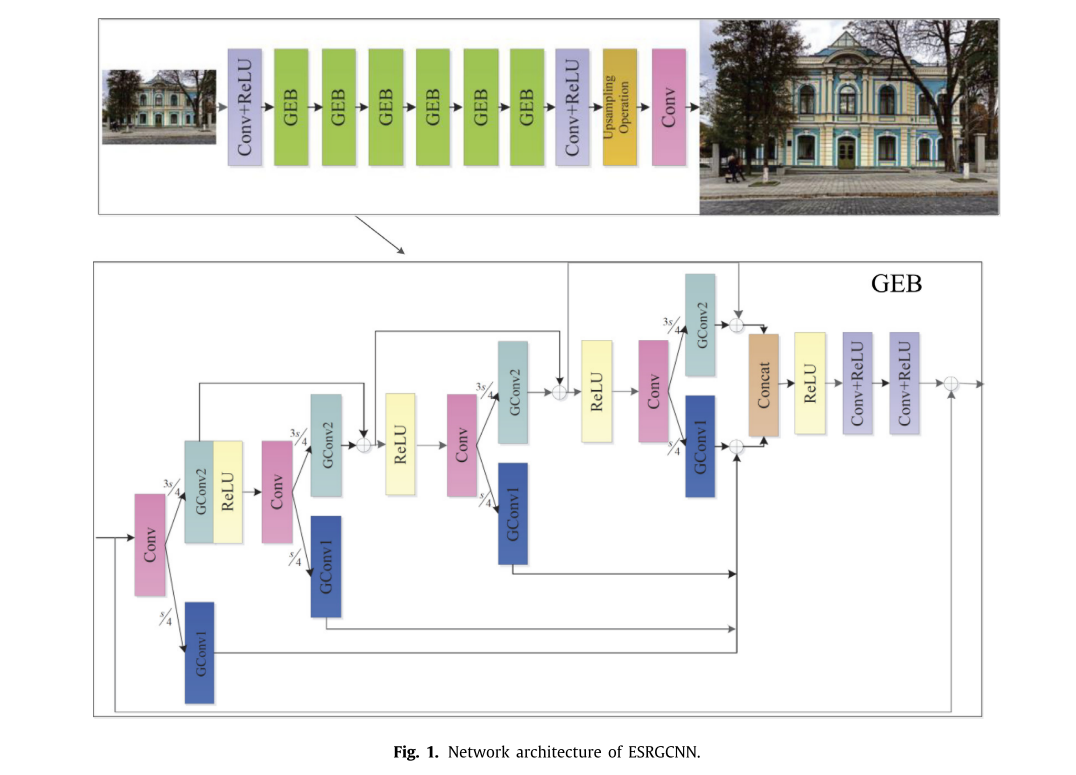

方法

我们提出的ESRGCNN包含三个卷积层、六个已知GEB的组卷积块和自适应上采样机制，如图1所示。具体地，基于GEB的群卷积和RL技术根据不同信道的相关性，融合宽和深信道特征以增强低频特征的表示能力，从而提高SISR性能并降低复杂度。此外，在每个GEB中的信号增强可以获得长距离的上下文信息，以解决ESRGCNN的长期依赖问题。由于ESRGCNN的体系结构较浅，因此它对SISR具有较快的执行速度。此外，自适应上采样机制利用一个灵活的阀来处理不同尺度的LR图像，以实现灵活的SR模型。因此，所提出的ESRGCNN可以更好地应用于真实的的数字设备。

Network architecture

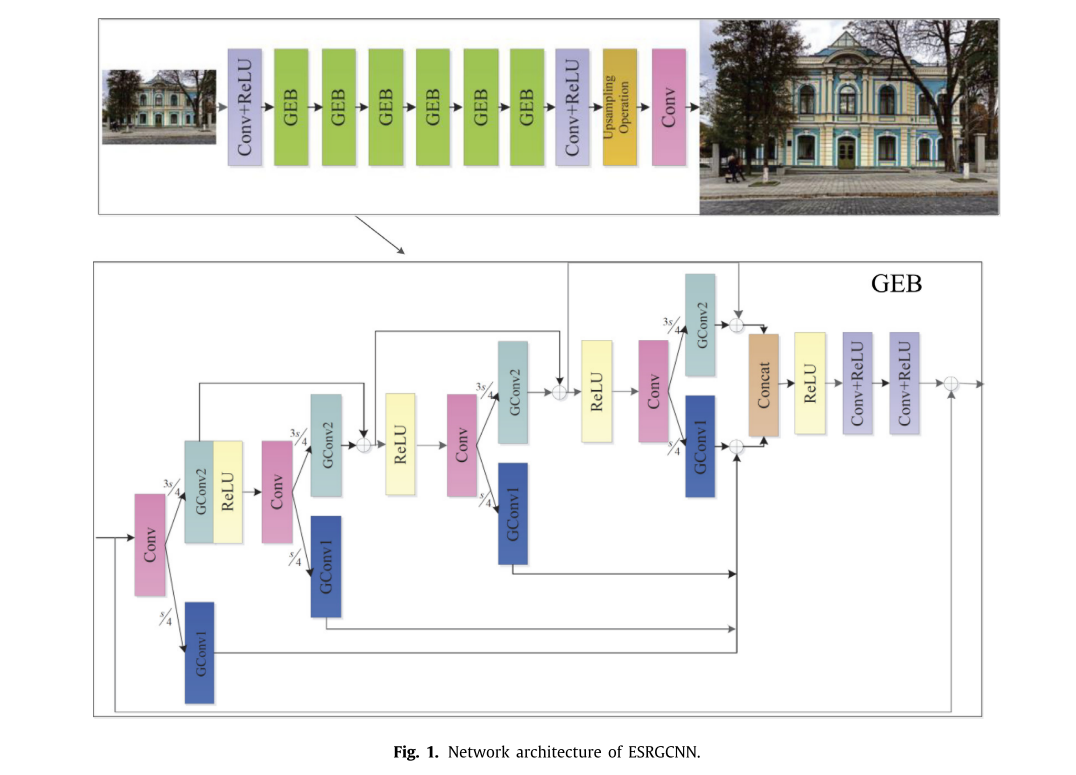
如图1所示，一个40层的ESRGCNN主要包括四个部分：卷积层和ReLU的2层组合（Krizhevsky，Sutskever，&欣顿，2012），36层GEB，1层上采样机制和单个卷积层。卷积层和ReLU的每个组合是卷积层连接ReLU，ReLU分别充当整个ESRGCNN的头部和中间。它们在图1中用Conv+ReLU表示。具体来说，第一个Conv+ReLU使用卷积层来获得给定的不清晰图像的关键信息，然后它连接激活函数ReLU（Krizhevsky等人）将获得的线性特征转化为非线性，其输入通道数、输出通道数和滤波器尺寸分别为3、64和3 × 3。此后，为了获得令人印象深刻的结果和具有竞争力的SISR复杂度，使用了6个GEB，每个GEB的输入通道数、输出通道数和滤波器大小分别为64、64和3 × 3，通过不同通道的相关性来增强低频特征的表达能力。同时，对每个GEB进行信号增强操作，提取长距离上下文信息，解决深度SR网络的长时间依赖问题。接下来，卷积层和ReLU的第二组合用于防止从上述操作获得的特征点像素的过度增强。具体地说，其通道号、输出通道号和滤波器大小与每个GEB相同。然后，该自适应上采样操作使用灵活的阈值来将提取的低频信息转换为高频信息，以实现灵活的SR模型。最后，ESRGCNN的最后一层为单卷积层，其通道数为64，输出通道数为3，滤波器大小为3 × 3，利用所获得的高频特征构造预测SR图像。为了直观地表示所述过程，我们定义一些符号如下。我们假设给定的I_LR和I_SR分别表示ESRGCNN的输入和输出。设C和R分别是卷积函数和ReLU函数。6GEB代表六组增强卷积块的函数。并且UP表示上采样操作。因此，上述用公式可表示为

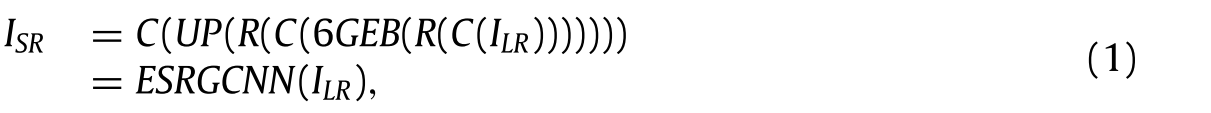
其中ESRGCNN代表ESRGCNN的函数

Loss function

本文选择公共均方误差（MSE）作为损失函数来确定用于预测SR图像的ESRGCNN的最佳参数。也就是说，将训练数据集的一组对{$I^k$_LR，$I^k$_HR}T_k=1用于MSE中以训练SR模型，其中$I^k$_LR和$I^k$_HR分别表示来自训练数据集的第k个低分辨率图像块和第k个高分辨率图像块。T表示训练图像块的总数。该过程如公式(2)所示：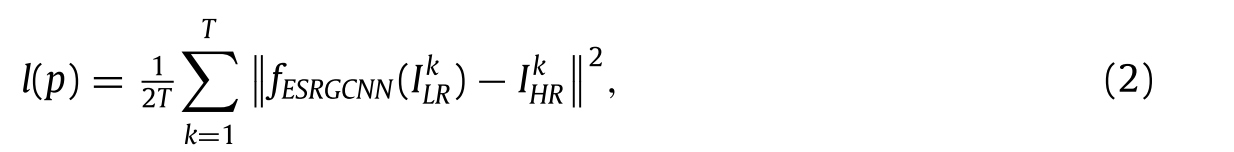
其中l用于表示损失函数MSE。p表示ESRGCNN模型中的参数集。

Group enhanced convolutional block

根据不同信道的相关性，采用6层分组增强卷积块增强低频特征的表示能力，提高SISR的性能和速度。同时考虑到网络设计原则，采用信号增强的思想继承长距离特征，解决深层网络浅层记忆能力较差的问题。GEB的详细信息如下所示。
已知现有的SR网络中有些直接增强深层特征，而没有充分利用不同信道的相关信息来提高SISR性能，计算代价较高。考虑到上述因素，我们使用组卷积将从每个GEB中的前四个卷积层获得的特征分成两组：GConv1为提取部分（当前卷积层获取特征的通道数的四分之一），GConv2为剩余部分（当前卷积层获取特征的通道数的四分之三），如图1所示。GConv1是输入通道数为16、输出通道数为16、滤波器尺寸为3 × 3的群卷积。GConv2是输入通道数为48、输出通道数为48、滤波器大小为3 × 3的群卷积。具体地说，只选择剩余部分作为主网络中下一卷积层的输入来提取更深层的特征，这可以提高SR模型的训练效率。与大多数随机共振方法不同的是，只有融合GEB中相邻的两个GConv2才能增强深邻域信息的作用，从而提高低频特征的表达能力。此外，除第一提取部分外的提取部分间接依赖于先前的剩余部分，融合这些提取的特征可以为深层的剩余部分提供互补的宽信息，从而提高SISR性能。为了生动地描述每个GConv1和GConv2的上述实现，我们将上述过程公式化如下。
同时学习各组的这些特征，并将它们融合，以加强它们之间的联系，从而提高低频特征的表达能力，具体步骤如下：
第一步融合通过RL技术获得的两个相邻GConv2的特征作为下一个卷积层的输入，以便在增强SISR中相邻层的特征方面促进来自不同通道的更准确的深度特征。具体地，来自不同GEB的第一GConv2的输出可以表示为

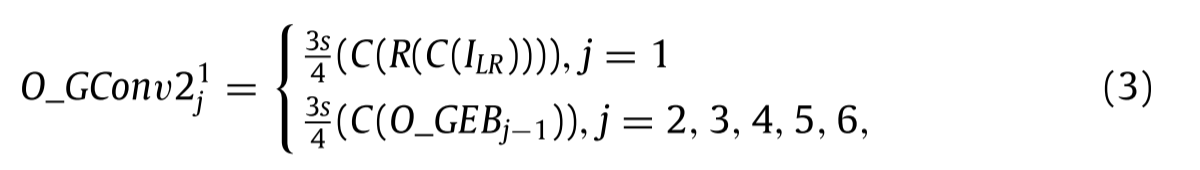
其中O_GEB~j − 1~表示第j − 1个GEB的输出。此外，O_GConv$2^1$_j是来自第j个GEB的第一个GConv2的输出。3s/4表示卷积层的剩余信道号，其中s是64。此外，来自不同GEB的其他GConv2的输出可以表示为：

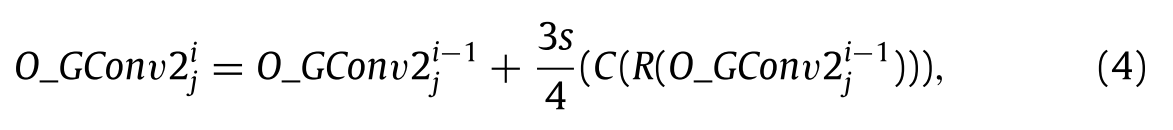
其中，O_GConv$2^i$_j表示第i个GConv2在第j个GEB中的输出。此外，i = 2、3、4，并且j = 1、2、3、4、5、6。具体来说，加号表示RL操作，在图1中也表示为⊕。
与GConv2不同，GEB中的第一个GConv1的输出可以通过来自第一卷积层的输出信道的最后四分之一获得。GEB中其他GConv1的输出由上层GConv2获得。即，上部GConv2连接ReLU以将线性特征转换为非线性。然后，将非线性作为卷积层进一步学习低频特征。从所述卷积层获得的特征的输出信息的最后四分之一信道作为GConv1的输入。这可以表示为方程(5)和(6):
第二步使用RL技术来合并从所有GConv1获得的特征，以如下加强不同蒸馏部分的连接: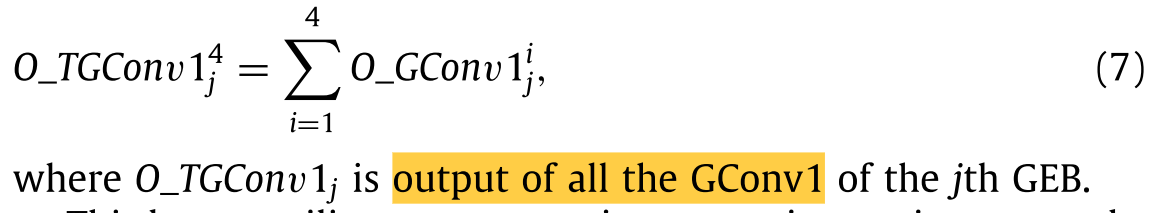
第三步骤利用级联操作来根据信道对从最后的GConv1和GConv2获得的特征进行积分，以获得更多的互补特征，其使用等式(8)以表达上述过程: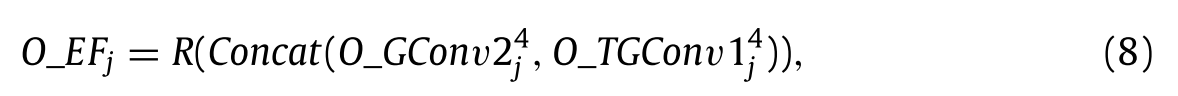
其中O_EF_j是来自第j个GEB的增强特征的输出。其输出通道数为64。此外，Concat表示式(8)和图1中的级联运算。此外，O_EF_j充当Conv+ReLU的两层，Conv+ReLU表示连接ReLU激活函数的卷积层。每层的输入通道数、输出通道数和滤波器尺寸分别为64、64和3 × 3。可以表示为
由于网络结构较深，浅层对深层的影响可能会减弱。受此启发，我们采用信号增强的思想来继承长距离特征，以解决整个网络浅层的记忆能力问题。也就是说，通过RL技术将获得的浅层的特征叠加在获得的深层的特征上，以提高SISR中浅层的重要性。上述课用公式表示为等式(10):
其中O_GEB_j代表第j个GEB的输出，j = 2，3，4，5，6。具体地，O_GEB₁ =O_DF₁ + R(C(I_LR))。此外，O_GEB₆充当Conv + ReLU，如公式(11)，用于防止方程（10）:

其中，OCR表示最后一个Conv+ReLU的输出，是上采样层的输入。

Adaptive upsampling mechanism

众所周知，一些流行的随机共振方法使用单个特定尺度的模型。然而，LR图像实际上是未知的损坏。受此启发，我们使用具有柔性阀的自适应上采样机制以从不同尺度的LR图像获得高质量图像，从而实现灵活的SR模型，如下所述：
自适应上采样机制由来自不同尺度的三种模式组成（即，×2、×3和×4）。这三种模式包括一个Conv+Shuffle ×2（称为×2模式）、一个Conv+Shuffle ×3（称为×3模式）和两个Conv+Shuffle ×2（称为×4模式），其中Conv+Shuffle ×2和Conv+Shuffle ×3分别表示3 × 3的卷积和Shuffle ×2和Shuffle ×3。×4模由两个叠加的×2模组成。此外，来自这些卷积的输入和输出的输入信道数是64。具体地，这些模式依赖于阀来实现盲SR模式。当阀值设置为0时，三种模式并行工作，训练出一个×2、×3和×4的SR模型，如图2所示。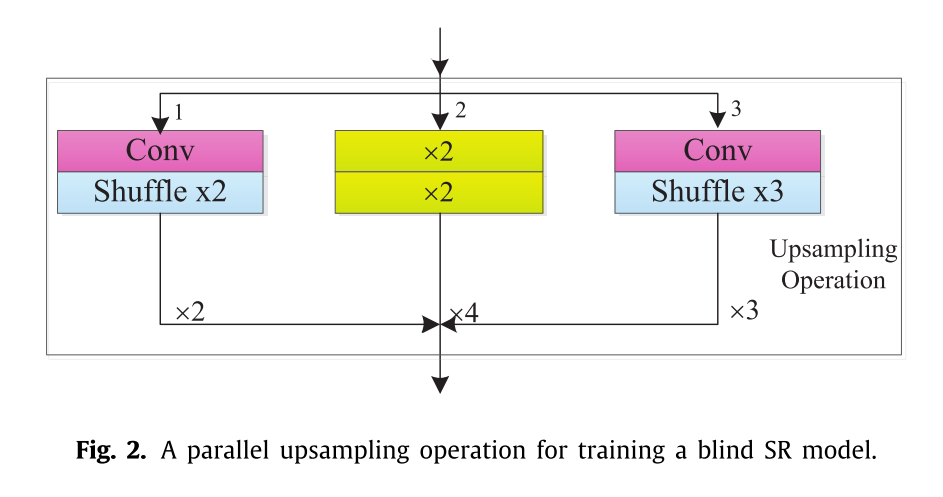
当阀门仅设置为2、3、4中的一种时，选择三种模式中的一种来测试图3中的blind SR模型。

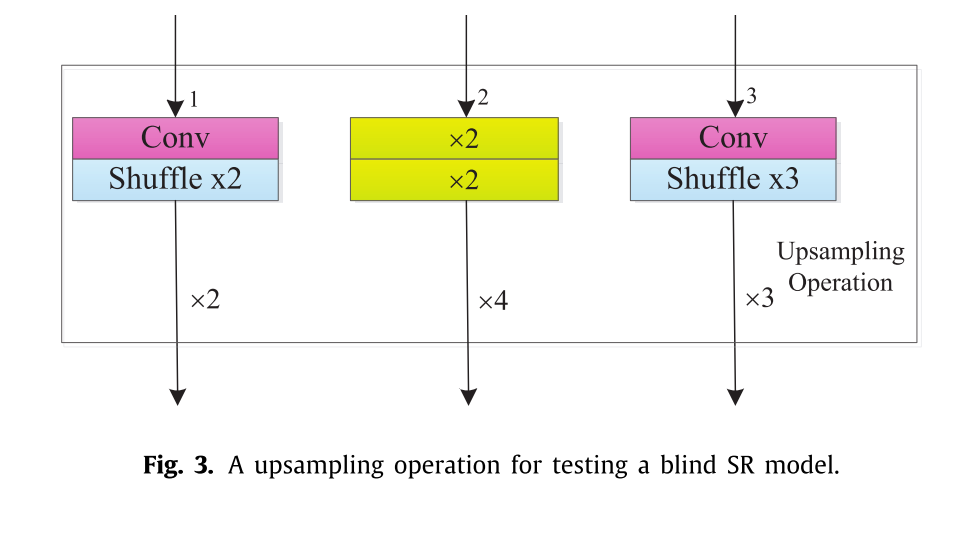
此外，上采样技术的函数可以使用等式(12)以代表所提及的过程：

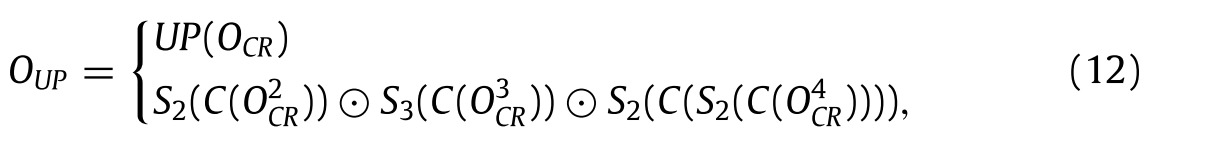
其中O_UP表示上采样层的输出。S₂、S₃和S₄分别表示混洗×2、混洗×3和混洗×4的函数。$O^2$_CR、$O^3$_CR和$O^4$_CR分别是从×2、×3和×4获得的低频信息的输出。此外，令⊙表示Pytorch中张量的拼接运算。此外，OUP是等式1中的最后卷积层的输入。(13)，其用于构造预测的SR图像。其输入数为64，输出数为3，滤波器尺寸为3 × 3。