提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

一、消失的数字
二、旋转数组

---

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、消失的数字

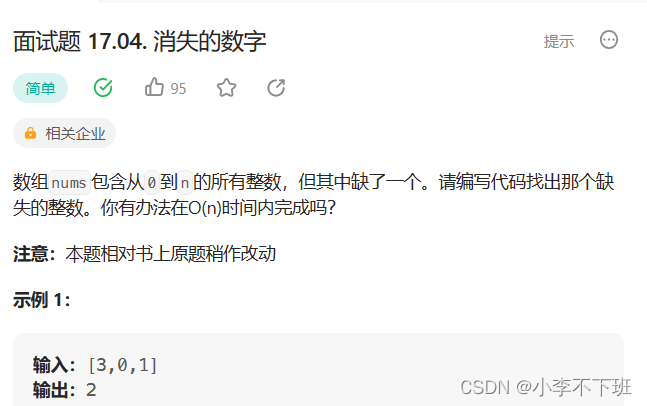
这题找出消失的一个数字，俗称找单身狗，要求时间复杂度为O(n)
这题我有两种题解
（1）用按位异或 ^ 操作
^ :两个数的二进制位异或，二进制位相同为0，相异为1如：
x = 1, y = 2
x 的二进制位表示为00000000 00000000 00000000 00000001
y的二进制位表示为00000000 00000000 00000000 00000010
x^y = 00000000 00000000 00000000 00000011 表示为十进制为 x^y=3
而这道题可以用按位异或来求解，先创建一个常量tmp = 0,tmp与nums数组中第一个元素异或得到的结果再依次与下一个异或，直到异或完数组中全部内容，将得出的结果再与从0~n中每一个整数异或，最后得出那个单身狗。

int missingNumber(int* nums, int numsSize)
{
    int tmp = 0;
    for (int i = 0; i < numsSize; i++)
    {

        tmp ^= nums[i];
    }
    for (int i = 0; i <=numsSize; i++)//由于数组内容从0~n消失了一个，那么在从0~n的整数中就要多一个
    {
        tmp ^= i;
    }

    return tmp;
}

第二种方法是将从0~n内的所有整数加起来再减去原数组之和，最后得出消失的那个数字

```c
int missingNumber(int* nums, int numsSize)
{
    int i = 0;
    
    int sum1 = 0;
    int sum = 0;
    for (i = 0; i <= numsSize; i++)//先求出0~n之和
    {

        sum1 = sum1 + i;
    }
    
    for (i = 0; i < numsSize; i++)
    {
        sum1 = sum1 - *(nums + i);//0~n整数和依次减去数组每一位最后结果返回
    }

    return sum1;
}

二、轮转数组

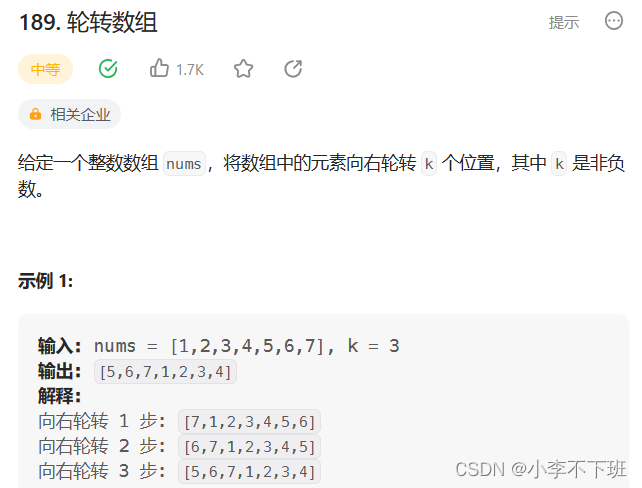
给定一个数字k，将数组轮转k次，在这里轮转的时候切记不可重复轮转，也就是k <= n，当k>n时要做取模运算
这题可以一个个旋转，就是创建一个变量将数组最后一个数存储起来，然后数组每一个元素向后挪，空出第一个位置，将存储起来的值赋给空出来的那个位置，循环k次，但是这样时间复杂度达到O(n^2)不可取题中要求时间复杂度为O（N),还有一种是再开一个数组，将要轮转的数依次取到新开的数组中，然后再将源数组从0~numsSize-k-1取到新数组中，最后将新数组中的元素更换到源数组中，但是这样就以空间换取时间，不是最优的，下面分区间逆置，然后再总体逆置，达到轮转数组的效果
上代码

void reserve(int* nums, int left, int right)
{
    while(left<right)
    {

    int tmp = nums[left];
    nums[left] = nums[right];
    nums[right] = tmp;
    left++;
    right--;

    }

}

void rotate(int *nums, int numsSize, int k)
{
    if(k>numsSize)
    {
        k=k%numsSize;
    }
//分区间逆置
    reserve(nums, numsSize-k, numsSize-1);
    reserve(nums, 0, numsSize-k-1);
    reserve(nums, 0, numsSize-1);

}

数组整体是这样的
分区间逆置numsSize-k~numsSize-1后变为

然后区间逆置0~numsSize-k-1后变为

然后再总体逆置

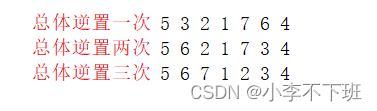
一下是逆置函数

```c
void reserve(int* nums, int left, int right)
{
    while(left<right)//控制逆置次数
    {
     //交换
    int tmp = nums[left];
    nums[left] = nums[right];
    nums[right] = tmp;
    left++;
    right--;

    }

}

---

# 总结
我的题解也许有诸多不足，请各位大佬帮忙指正