目录

一.B树概念

二.B树插入思路

二.B树分部实现

1.树节点类

2.B树成员结构

3.查找函数

4.插入函数（核心）

5.插入关键值

6.中序遍历（有序）

三.B树实现总代码

四.B树性能分析

五.B+树和B*树

1.B+树

2.B*树

3.总结

六.B树应用

1.索引

2.MySQL索引简介

（1）MyISAM

（2）InnoDB

---

        前言：之前学过AVL树、红黑树、哈希表等，这些都是用作内查找（内存数据查找）的，而B树系列则是用于外查找（磁盘数据查找）的。B树的结构要更为复杂一些。

一.B树概念

        B树是一种平衡的多叉树，适合外查找。一棵m阶（m > 2）的B树，是一棵平衡的M路平衡搜索树（也可以是空树）。

        性质：
① 根结点至少有两个孩子

② 每个分支结点都包含k-1个关键字和k个孩子，其中m/2 <= k <= m

③ 每个叶子结点都包含k-1个关键字，其中m/2 <= k <= m

④ 所有的叶子结点都在同一层

⑤ 每个结点中的关键字从小到大排列，结点当中k-1个元素正好是k个孩子包含的元素的值域划分

⑥ 每个结点的结构为：n，A0，K1，A1，K2，A2，... ，Kn，An。其中，Ki(1≤i≤n)为关键字，且Ki < Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数，满足m/2-1 ≤ n ≤ m-1。

二.B树插入思路

1. 如果树为空，直接插入新节点中，使该节点为树的根节点

2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)

3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)

4. 按照插入排序的思想将该元素插入到找到的节点中

5. 检测该节点是否满足B树的性质：即该节点中的元素个数是否小于M，如果小于则满足

6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：

分裂方法：

① 申请新节点
② 找到该节点的中间位置
③ 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
④ 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续步骤4

7. 如果向上已经分裂到根节点的位置，插入结束

 

二.B树分部实现

1.树节点类

        模板中K是存的数据类型，M是阶数（chu），这里创建一个存孩子的数组指针变量，一个存孩子的指针变量，这里为了方便插入以后分裂，要多开一个空间，

template<class K, size_t M>
struct BTreeNode
{
	// 为了方便插入以后再分裂，多给一个空间
	K _keys[M];
	BTreeNode<K, M>* _subs[M + 1];
	BTreeNode<K, M>* _parent;

	size_t _n; // 记录实际存储的多个关键字

	BTreeNode()
	{
		for (size_t i = 0; i < M; ++i)
		{
			_keys[i] = K();
			_subs[i] = nullptr;
		}

		_subs[M] = nullptr;
		_parent = nullptr;
		_n = 0;
	}
};

2.B树成员结构

template<class K, size_t M>
class BTree
{
	typedef BTreeNode<K, M> Node;
public:

private:
	Node* _root = nullptr;
};

3.查找函数

        查找函数利用B树的特定，如果要查找的值比当前值小，就要走到它的左孩子，这里是通过break跳出在后面跳到左孩子；如果要查找的值比当前值大，就先向右走，后面循环就可能遇到比要查找的值还大的值，这就要到上面的if中然后break出，从而往左孩子跳了。最后即使没找到，也要带回叶子结点，为了方便插入函数进行插入。

pair<Node*, int> Find(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)
	{
		// 在一个结点查找
		size_t i = 0;
		while (i < cur->_n)
		{
			// key比该值小，要走到它的左孩子，break后在外面跳到它的左孩子
			if (key < cur->_keys[i])
			{
				break;
			}
			// key比该值大，先向右走
			// 后面可能会循环到上面的if中往左孩子跳或者找到了
			else if (key > cur->_keys[i])
			{
				++i;
			}
			else
			{
				return make_pair(cur, i);
			}
		}

		// 往孩子那去跳
		parent = cur;
		cur = cur->_subs[i];
	}

	// 没找到，带回叶子结点
	return make_pair(parent, -1);
}

4.插入函数（核心）

        这里插入函数就需要考虑空树，插入后满了需要分裂的情况。

        首先空树，插入第一个结点，并作为根。

        非空树，就先查找要插入的key是否已经存在，如果存在就不允许插入，如果不存在，那么这里因为调用了Find函数，Find带回了要插入的那个叶子结点，然后进行插入操作。

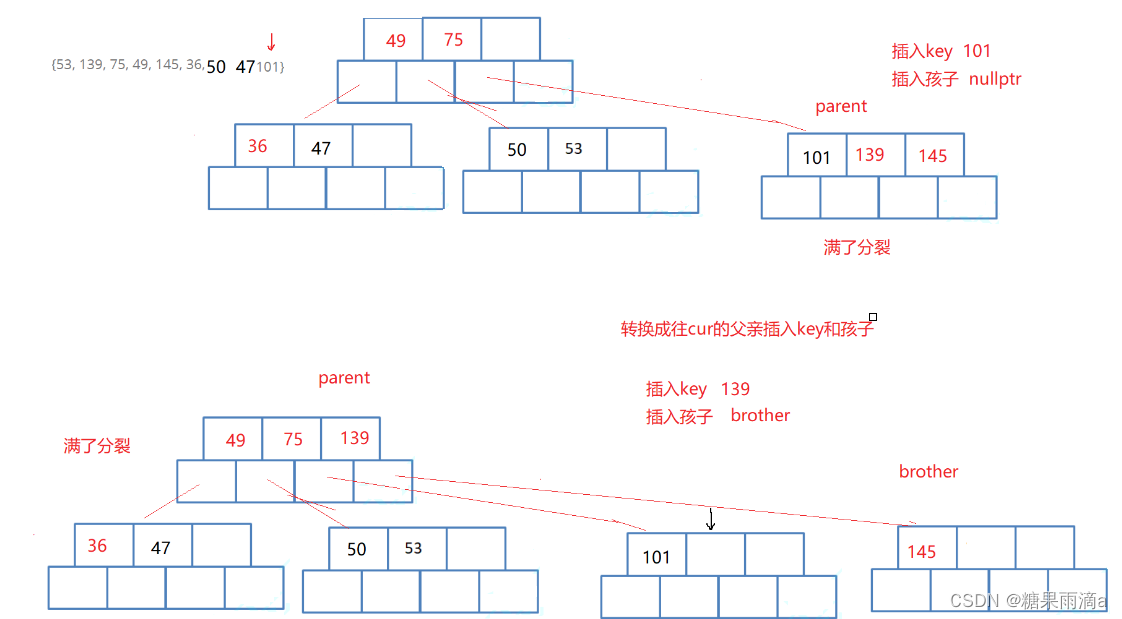
        这里我们不确定要进行几次分裂，因此写一个循环，然后先根据插入值函数把该key插入到对应的位置上。接下来去判断是否满了，如果没满，就直接结束；如果满了，就要进行分裂操作。

        分裂是要把这个满了的分裂一半给新创建的兄弟，这里再分裂时要拷贝key和key的左孩子，同时完成相对应的链接操作，再把拷贝走的重置掉。这时剩的最后一个右孩子也要拷走，并进行链接。之后再完成相对应的更新，更新存储的关键值等。这时要注意，我们要保存刚刚分裂的中间的那个结点，因为这个结点是要往上走，插入到上面的。这里也要进行判断，如果刚刚分裂的时根结点，那么这个分裂的中间结点就会变成新的根结点；如果不是，就先保存，然后往上走，在下一个循环中就会通过InsertKey函数插入到上面了。

bool Insert(const K& key)
{
	// B树为空时，插入第一个结点
	if (_root == nullptr)
	{
		_root = new Node;
		_root->_keys[0] = key;
		_root->_n++;

		return true;
	}

	// key已经存在，不允许插入
	pair<Node*, int> ret = Find(key);
	// 只要不为-1，就找到了
	if (ret.second >= 0)
	{
		return false;
	}

	// 如果没有找到，find带回了要插入的那个叶子结点

	// 循环每次往cur插入newkey和child
	Node* parent = ret.first;
	K newKey = key;
	Node* child = nullptr;
	while (1)
	{
		InsertKey(parent, newKey, child);
		// 插入后满了就要分裂
		// 没有满，插入就结束
		if (parent->_n < M)
		{
			return true;
		}
		else
		{
			size_t mid = M / 2;
			// 分裂一半给兄弟
			Node* brother = new Node;
			size_t j = 0;
			size_t i = mid + 1;
			for (; i <= M - 1; ++i)
			{
				// 分裂拷贝key和key的左孩子
				// 分裂时不仅要带走key，也要把其对应的左孩子带走
				brother->_keys[j] = parent->_keys[i];
				brother->_subs[j] = parent->_subs[i];
				// 有带走的孩子时，就要将带走的孩子重新链接到新的的brother中
				if (parent->_subs[i])
				{
					parent->_subs[i]->_parent = brother;
				}
				++j;

				// 拷走的就重置一下，方便观察
				parent->_keys[i] = K();
				parent->_subs[i] = nullptr;
			}
				
			// 还有最后一个右孩子也要拷走
			brother->_subs[j] = parent->_subs[i];
			// 有带走的孩子时，就要将带走的孩子重新链接到新的的brother中
			if (parent->_subs[i])
			{
				praent->subs[i]->_parent = brother;
			}
			parent->_subs[i] = nullptr;

			// 更新brother和parent实际存储的关键字_n
			brother->_n = j;
			parent->_n -= (brother->_n + 1);

			// 保存分裂的中间结点，并将中间结点重置
			// 为接下来将该中间结点往上走做准备
			K midKey = parent->_keys[mid];
			parent->_keys[mid] = K();

			// 刚刚分裂的是根结点，分裂的中间结点变成新的根结点
			if (parent->_parent == nullptr)
			{
				_root = new Node;
				_root->_keys[0] = midKey;
				_root->_subs[0] = parent;
				_root->_subs[1] = brother;
				_root->_n = 1;

				parent->_parent = _root;
				brother->_parent = _root;
				break;
			}
			// 刚刚分裂的不是根结点
			else
			{
				// 先保存，往上走，在下一次循环中，通过InsertKey插入到上面
				newKey = midKey;

				child = brother;
				parent = parent->_parent;
			}
		}
	}

	return true;
}

5.插入关键值

        这个就是把值插入进去，不进行分裂等其它操作的一个子函数。这里如果要插入的值比下一个小，就挪动key和它的右孩子，如果不一起挪会导致链接出错。挪动好之后，就在对应的位置插入key，并链接上新的孩子，也让孩子链接上新的key。

void InsertKey(Node* node, const K& key, Node* child)
{
	int end = node->_n - 1;
	while (end >= 0)
	{
		if (key < node->_keys[end])
		{
			// 挪动key和它的右孩子
			// 注意key和右孩子要一起挪，否则连接就出错了
			node->_keys[end + 1] = node->_keys[end];
			node->_subs[end + 2] = node->_subs[end + 1];
			--end;
		}
		else
		{
			break;
		}
	}

	// 前面挪动好之后，在正确的位置插入key
	node->_keys[end + 1] = key;
	node->_subs[end + 2] = child;
	if (child)
	{
		child->_parent = node;
	}

	node->_n++;
}

6.中序遍历（有序）

        左根 左根 ... 右的利用递归进行遍历。

void _InOrder(Node* cur)
{
    if (cur == nullptr)
		return;

	size_t i = 0;
	for (; i < cur->_n; ++i)
	{
		_InOrder(cur->_subs[i]); // 左子树
		cout << cur->_keys[i] << " "; // 根
	}

	_InOrder(cur->_subs[i]); // 最后的那个右子树
}

void InOrder()
{
	_InOrder(_root);
}

三.B树实现总代码

#pragma once

template<class K, size_t M>
struct BTreeNode
{
	// 为了方便插入以后再分裂，多给一个空间
	K _keys[M];
	BTreeNode<K, M>* _subs[M + 1];
	BTreeNode<K, M>* _parent;

	size_t _n; // 记录实际存储的多个关键字

	BTreeNode()
	{
		for (size_t i = 0; i < M; ++i)
		{
			_keys[i] = K();
			_subs[i] = nullptr;
		}

		_subs[M] = nullptr;
		_parent = nullptr;
		_n = 0;
	}
};

// 数据是存在磁盘的，K是磁盘地址
template<class K, size_t M>
class BTree
{
	typedef BTreeNode<K, M> Node;
public:
	pair<Node*, int> Find(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			// 在一个结点查找
			size_t i = 0;
			while (i < cur->_n)
			{
				// key比该值小，要走到它的左孩子，break后在外面跳到它的左孩子
				if (key < cur->_keys[i])
				{
					break;
				}
				// key比该值大，先向右走
				// 后面可能会循环到上面的if中往左孩子跳或者找到了
				else if (key > cur->_keys[i])
				{
					++i;
				}
				else
				{
					return make_pair(cur, i);
				}
			}

			// 往孩子那去跳
			parent = cur;
			cur = cur->_subs[i];
		}

		// 没找到，带回叶子结点
		return make_pair(parent, -1);
	}

	void InsertKey(Node* node, const K& key, Node* child)
	{
		int end = node->_n - 1;
		while (end >= 0)
		{
			if (key < node->_keys[end])
			{
				// 挪动key和它的右孩子
				// 注意key和右孩子要一起挪，否则连接就出错了
				node->_keys[end + 1] = node->_keys[end];
				node->_subs[end + 2] = node->_subs[end + 1];
				--end;
			}
			else
			{
				break;
			}
		}

		// 前面挪动好之后，在正确的位置插入key
		node->_keys[end + 1] = key;
		node->_subs[end + 2] = child;
		if (child)
		{
			child->_parent = node;
		}

		node->_n++;
	}

	bool Insert(const K& key)
	{
		// B树为空时，插入第一个结点
		if (_root == nullptr)
		{
			_root = new Node;
			_root->_keys[0] = key;
			_root->_n++;

			return true;
		}

		// key已经存在，不允许插入
		pair<Node*, int> ret = Find(key);
		// 只要不为-1，就找到了
		if (ret.second >= 0)
		{
			return false;
		}

		// 如果没有找到，find带回了要插入的那个叶子结点

		// 循环每次往cur插入newkey和child
		Node* parent = ret.first;
		K newKey = key;
		Node* child = nullptr;
		while (1)
		{
			InsertKey(parent, newKey, child);
			// 插入后满了就要分裂
			// 没有满，插入就结束
			if (parent->_n < M)
			{
				return true;
			}
			else
			{
				size_t mid = M / 2;
				// 分裂一半给兄弟
				Node* brother = new Node;
				size_t j = 0;
				size_t i = mid + 1;
				for (; i <= M - 1; ++i)
				{
					// 分裂拷贝key和key的左孩子
					// 分裂时不仅要带走key，也要把其对应的左孩子带走
					brother->_keys[j] = parent->_keys[i];
					brother->_subs[j] = parent->_subs[i];
					// 有带走的孩子时，就要将带走的孩子重新链接到新的的brother中
					if (parent->_subs[i])
					{
						parent->_subs[i]->_parent = brother;
					}
					++j;

					// 拷走的就重置一下，方便观察
					parent->_keys[i] = K();
					parent->_subs[i] = nullptr;
				}
				
				// 还有最后一个右孩子也要拷走
				brother->_subs[j] = parent->_subs[i];
				// 有带走的孩子时，就要将带走的孩子重新链接到新的的brother中
				if (parent->_subs[i])
				{
					praent->subs[i]->_parent = brother;
				}
				parent->_subs[i] = nullptr;

				// 更新brother和parent实际存储的关键字_n
				brother->_n = j;
				parent->_n -= (brother->_n + 1);

				// 保存分裂的中间结点，并将中间结点重置
				// 为接下来将该中间结点往上走做准备
				K midKey = parent->_keys[mid];
				parent->_keys[mid] = K();

				// 刚刚分裂的是根结点，分裂的中间结点变成新的根结点
				if (parent->_parent == nullptr)
				{
					_root = new Node;
					_root->_keys[0] = midKey;
					_root->_subs[0] = parent;
					_root->_subs[1] = brother;
					_root->_n = 1;

					parent->_parent = _root;
					brother->_parent = _root;
					break;
				}
				// 刚刚分裂的不是根结点
				else
				{
					// 先保存，往上走，在下一次循环中，通过InsertKey插入到上面
					newKey = midKey;

					child = brother;
					parent = parent->_parent;
				}
			}
		}

		return true;
	}

	void _InOrder(Node* cur)
	{
		if (cur == nullptr)
			return;

		size_t i = 0;
		for (; i < cur->_n; ++i)
		{
			_InOrder(cur->_subs[i]); // 左子树
			cout << cur->_keys[i] << " "; // 根
		}

		_InOrder(cur->_subs[i]); // 最后的那个右子树
	}

	void InOrder()
	{
		_InOrder(_root);
	}
private:
	Node* _root = nullptr;
};

四.B树性能分析

        对于一棵节点为N度为M的B树，查找和插入需要$log{M-1}N$~$log{M/2}N$次比较，这个很好证明：对于度为M的B树，每一个节点的子节点个数为M/2 ~(M-1)之间，因此树的高度应该在要log{M-1}N和log{M/2}N之间，在定位到该节点后，再采用二分查找的方式可以很快的定位到该元素。
        B树的效率是很高的，对于N = 62*1000000000个节点，如果度M为1024，log_{M/2}N <=4，即在620亿个元素中，如果这棵树的度为1024，则需要小于4次即可定位到该节点，然后利用二分查找可以快速定位到该元素，大大减少了读取磁盘的次数。

        B树一般四层就够了，可以读取到足够多的数据了。

五.B+树和B*树

1.B+树

        B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又在B树的基础上做了以下几点改进优化：

① 分支节点的子树指针与关键字个数相同

② 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间

③ 所有叶子节点增加一个链接指针链接在一起

④ 所有关键字及其映射数据都在叶子节点出现

        B+树特性：

① 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的

② 不可能在分支节点中命中

③ 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。
 

2.B*树

        B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

        所以，与B+树比较，B*树分配新结点的概率比B+树要低，空间使用率更高。

3.总结

B树：有序数组+平衡多叉树；
B+树：有序数组链表+平衡多叉树；
B*树：一棵更丰满的，空间利用率更高的B+树。

在实际使用中，B+的使用是最多的。

六.B树应用

1.索引

        B树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物，比如：书籍目录可以让读者快速找到相关信息；网页的导航网站，为了让用户能够快速的找到有价值的分类网站。本质上就是互联网页面中的索引结构。

        MySQL官方对索引的定义为：索引(index)是帮助MySQL高效获取数据的数据结构，简单来说：索引就是数据结构。

        当数据量很大时，为了能够方便管理数据，提高数据查询的效率，一般都会选择将数据保存到数据库，因此数据库不仅仅是帮助用户管理数据，而且数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用数据，这样就可以在这些数据结构上实现高级查找算法，该数据结构就是索引。

2.MySQL索引简介

        MySQL是目前非常流行的开源关系型数据库，不仅是免费的，可靠性高，速度也比较快，而且拥有灵活的插件式存储引擎

        MySQL中索引属于存储引擎级别的概念，不同存储引擎对索引的实现方式是不同的。

（1）MyISAM

        MyISAM引擎是MySQL5.5.8版本之前默认的存储引擎，不支持事务，支持全文检索，使用B+Tree作为索引结构，叶节点的data域存放的是数据记录的地址，其结构如下：

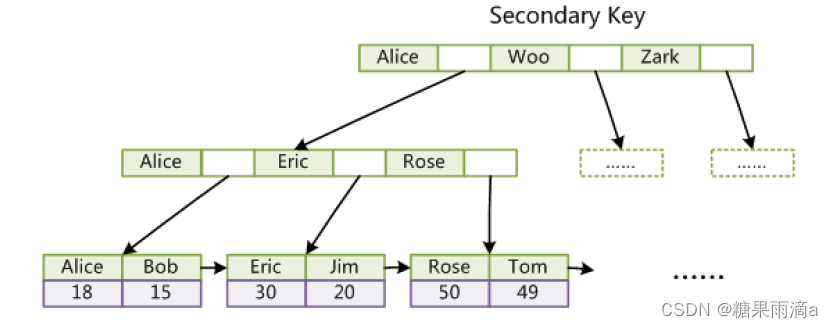
        上图是以以Col1为主键，MyISAM的示意图，可以看出MyISAM的索引文件仅仅保存数据记录的地址。在MyISAM中，主索引和辅助索引（Secondary key）在结构上没有任何区别，只是主索引要求key是唯一的，而辅助索引的key可以重复。如果想在Col2上建立一个辅助索引，则此索引的结构如下图所示：

        同样也是一棵B+Tree，data域保存数据记录的地址。因此，MyISAM中索引检索的算法为首先按照B+Tree搜索算法搜索索引，如果指定的Key存在，则取出其data域的值，然后以data域的值为地址，读取相应数据记录。MyISAM的索引方式也叫做“非聚集索引”的

（2）InnoDB

        InnoDB存储引擎支持事务，其设计目标主要面向在线事务处理的应用，从MySQL数据库5.5.8版本开始，InnoDB存储引擎是默认的存储引擎。InnoDB支持B+树索引、全文索引、哈希索引。但InnoDB使用B+Tree作为索引结构时，具体实现方式却与MyISAM截然不同。

        第一个区别是InnoDB的数据文件本身就是索引文件。MyISAM索引文件和数据文件是分离的，索引文件仅保存数据记录的地址。而InnoDB索引，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键，因此，InnoDB表数据文件本身就是主索引。

        上图是InnoDB主索引（同时也是数据文件）的示意图，可以看到叶节点包含了完整的数据记录，这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集，所以InnoDB要求表必须有主键（MyISAM可以没有），如果没有显式指定，则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键，如果不存在这种列，则MySQL自动为InnoDB表生成一个隐含字段作为主键，这个字段长度为6个字节，类型为长整型。

        第二个区别是InnoDB的辅助索引data域存储相应记录主键的值而不是地址，所有辅助索引都引用主键作为data域。

        聚集索引这种实现方式使得按主键的搜索十分高效，但是辅助索引搜索需要检索两遍索引：首先检索辅助索引获得主键，然后用主键到主索引中检索获得记录。