目录
T1:迷宫 - 暴力dfs+标注
T2:跳蚱蜢 - 9数算式 全排列 + 枚举乘号位置
T3:魔方状态 - 模拟 + 判重 (高手入*****)
T4:方格分割 - dfs + 从中心点去切割
T5:字母组串 - 递归思维-搞清楚参数的含义和参数变化的方向
T6:最大公共子串 - 经典的dp问题
T7:正则问题 - 不规则递归
T8:包子凑数 - 扩展欧几里得+完全背包-dp 不定方程--递归 **
T9:分巧克力-暴力枚举/二分枚举 ——基本功
T10:油漆面积- 暴力打点法/线段树+扫描线+矩形面积
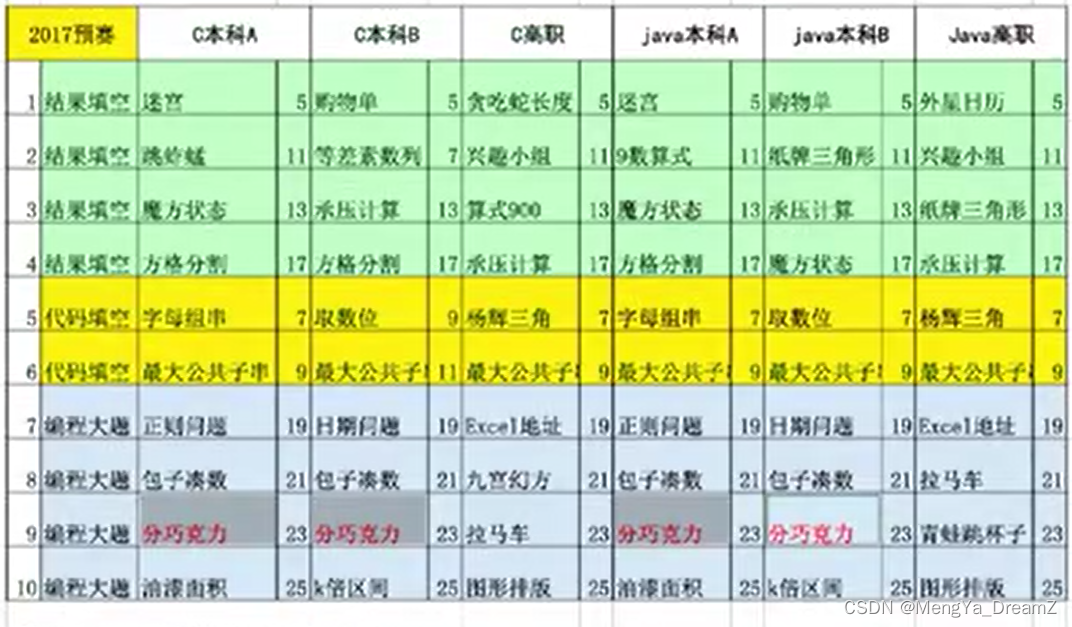
T1:迷宫 - 暴力dfs+标注
X星球的一处迷宫游乐场建在某个小山坡上。它是由10x10相互连通的小房间组成的。房间的地板上写着一个很大的字母。我们假设玩家是面朝上坡的方向站立,则:L表示走到左边的房间,R表示走到右边的房间,U表示走到上坡方向的房间,D表示走到下坡方向的房间。
X星球的居民有点懒,不愿意费力思考。他们更喜欢玩运气类的游戏。这个游戏也是如此!开始的时候,直升机把100名玩家放入一个个小房间内。
玩家一定要按照地上的字母移动。迷宫地图如下:
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR请你计算一下,最后,有多少玩家会走出迷宫? 而不是在里边兜圈子。 答案:31
考点:dfs+标注
标注:走出迷宫
小白重点:
- dfs 暴力伸收
- memset:
- 头文件 #include <string.h>
- memset(a,0,sizeof(a));
- 括号中分别是(数组名,要初始化的数,sizeof求数组的长度)
- 但是要注意,初始化不可以初始任何值,是因为memset初始化方式是是按字节
#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
string data[10];
int ans;
int vis[10][10];
bool solve(int i, int j){
//表明已不再区域中,走出迷宫
if(i<0||i>9||j<0||j>9)
return true;
//表明已经来过这个位置
if(vis[i][j]==1)
return false;
vis[i][j] =1;
//判断
switch(data[i][j]){
case 'U':
return solve(i-1,j);
case 'D':
return solve(i+1,j);
case 'L':
return solve(i,j-1);
case 'R':
return solve(i,j+1);
default:
return false;
}
}
int main(int argc, const char *argv[]){
data[0]= "UDDLUULRUL";
data[1]= "UURLLLRRRU";
data[2]= "RRUURLDLRD";
data[3]= "RUDDDDUUUU";
data[4]= "URUDLLRRUU";
data[5]= "DURLRLDLRL";
data[6]= "ULLURLLRDU";
data[7]= "RDLULLRDDD";
data[8]= "UUDDUDUDLL";
data[9]= "ULRDLUURRR";
for (int i=0; i<10; i++){
for(int j=0; j<10; j++){
//注意每一次深搜后都要重新将vis数组清零
memset(vis, 0, sizeof(vis));
bool res = solve(i, j);
if(res)
ans++;
}
}
cout << ans << endl;
return 0;
}#include<bits/stdc++.h>
using namespace std;
int vis[10][10];
int s[10][10];
int sum=0;
bool judge(int x,int y) {
if(x>=0&&x<10&&y>=0&&y<10) {
return false;
}
return true; //表明已经不再区域内,即成功走出迷宫
}
void dfs(int x,int y) {
if(judge(x,y)) { //走出迷宫
sum++;
return;
}
if(!vis[x][y]) {
vis[x][y]=1;
if(s[x][y]=='U'){
dfs(x-1,y);
}else if(s[x][y]=='D') {
dfs(x+1,y);
}else if(s[x][y]=='R') {
dfs(x,y+1);
}else if(s[x][y]=='L') {
dfs(x,y-1);
}
}
}
int main() {
int ct=0;
string str="UDDLUULRULUURLLLRRRURRUURLDLRDRUDDDDUUUUURUDLLRRUUDURLRLDLRLULLURLLRDURDLULLRDDDUUDDUDUDLLULRDLUURRR";
for(int i=0;i<10;i++) { //先分成而二维数组
for(int j=0;j<10;j++) {
s[i][j]=str[ct];
ct++;
}
}
for(int i=0;i<10;i++) {
for(int j=0;j<10;j++) {
memset(vis,0,sizeof(vis)); //注意每一次深搜后都要重新将vis数组清零
dfs(i,j);
}
}
cout<<sum;
return 0;
}
T2:跳蚱蜢 - 9数算式 全排列 + 枚举乘号位置
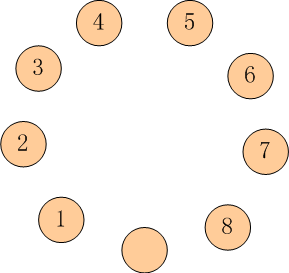
有9只盘子,排成1个圆圈。其中8只盘子内装着8只蚱蜢,有一个是空盘。
我们把这些蚱蜢顺时针编号为 1~8,每只蚱蜢都可以跳到相邻的空盘中,也可以再用点力,越过一个相邻的蚱蜢跳到空盘中。请你计算一下,如果要使得蚱蜢们的队形改为按照逆时针排列,并且保持空盘的位置不变(也就是1-8换位,2-7换位,…),至少要经过多少次跳跃?
注意:要求提交的是一个整数,请不要填写任何多余内容或说明文字。
考点:bfs
小白重点:
- 从一个状态到另一个状态需要多少步,BFS问题!
- BFS算法和DFS算法(含图解:简单易懂)
- 先将字符串012345678入队列,然后出队列,按照规则产生新的字符串,如果该字符串就是目标字符串那么就终止,如果不是且以前没有出现过,那么就入队列,重复上述操作即可。
- 【跳蚱蜢】2017年第八届蓝桥杯【C/C++省赛A组】
#include<bits/stdc++.h>
using namespace std;
struct state {
int pos,cnt; //pos记录当前空盘位置,cnt记数,表示走了几步
char *s; //当前字符串
state(int pos,char *s,int cnt):pos(pos),s(s),cnt(cnt){} //构造函数
};
struct cmp {
bool operator()(char *a,char *b) {
return strcmp(a,b)>0;
}
};
int change[4]={-1,-2,1,2},cnt=1; //change表示四个位置,左1左2,右1右2
char *start="012345678",*end="087654321";
queue<state> q;
set<char *,cmp> check;
void swap(char *s,int a,int b) {
char t=s[a];
s[a]=s[b];
s[b]=t;
}
int bfs() {
q.push(state(0,start,0)); //初始状态入队
while(!q.empty()) {
state temp=q.front(); //获取当前队头结点
int pos=temp.pos;
int cnt=temp.cnt;
char *s=temp.s;
check.insert(s);
if(strcmp(s,end)==0) { //已经找到就结束
cout<<cnt;
return 0;
}
q.pop();
//产生新字符串入队
for(int i=0;i<4;i++) {
char *t=(char*)malloc(9*sizeof(char));
strcpy(t,s);
int newpos=(pos+change[i]+9)%9; //交换后新的空盘位置
swap(t,pos,newpos); //交换
if(check.find(t)==check.end()) {
check.insert(t);
q.push(state(newpos,t,cnt+1)); //新结点入队
}
}
}
}
int main() {
bfs();
return 0;
}
T3:魔方状态 - 模拟 + 判重 (高手入*****)
二阶魔方就是只有2层的魔方,只由8个小块组成。如下所示:
小明很淘气,他只喜欢3种颜色,所有把家里的二阶魔方重新涂了颜色,如下:
前面:橙色
右面:绿色
上面:黄色
左面:绿色
下面:橙色
后面:黄色请你计算一下,这样的魔方被打乱后,一共有多少种不同的状态。
如果两个状态经过魔方的整体旋转后,各个面的颜色都一致,则认为是同一状态。
请提交表示状态数的整数,不要填写任何多余内容或说明文字。
T4:方格分割 - dfs + 从中心点去切割
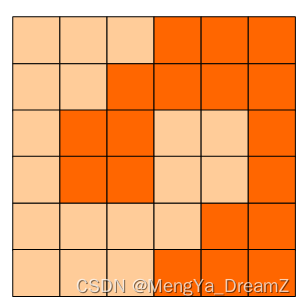
6x6的方格,沿着格子的边线剪开成两部分,要求这两部分的形状完全相同。如图:p1.png, p2.png就是可行的分割法。
试计算:包括这2种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。请提交该整数,不要填写任何多余的内容或说明文字。
思路延展:剪格子、剪邮票
考点:dfs + 标注
标注:剪到边了
关注切割线,延中心点
#include<iostream>
#include<string.h>
#include <stdio.h>
using namespace std;
int ans = 0;
int dire[][2]={ {-1,0},
{1,0},
{0,-1},
{0,1}};
int vis[7][7]; //记录点已访问
void dfs(int x, int y){
if(x==0||y==0||x==6||y==6){
ans++;
return;
}
//当前位置点标注为已访问
vis[x][y] = 1;
vis[6-x][6-y] = 1;
for(int k=0; k<4; ++k){
int nx = x + dire[k][0];
int ny = y + dire[k][1];
//新坐标,在范围内
if(nx<0||ny<0||nx>6||ny>6)continue;
if(!vis[nx][ny]){
dfs(nx,ny);
}
}
vis[x][y]=0;
vis[6-x][6-y]=0;
}
int main(int argc, const char *argv[]){
dfs(3,3);
cout << ans/4 <<endl;
return 0;
}T5:字母组串 - 递归思维-搞清楚参数的含义和参数变化的方向
由 A,B,C 这3个字母就可以组成许多串。比如:“A”,“AB”,“ABC”,“ABA”,“AACBB” …
现在,小明正在思考一个问题:如果每个字母的个数有限定,能组成多少个已知长度的串呢?
他请好朋友来帮忙,很快得到了代码,解决方案超级简单,然而最重要的部分却语焉不详。请仔细分析源码,填写划线部分缺少的内容。
考点:递归
#include<stdio.h>
using namespace std;
// a个A,b个B,c个C 字母,能组成多少个不同的长度为n的串。
int f(int a, int b, int c, int n)
{
if(a<0 || b<0 || c<0) return 0;
if(n==0) return 1;
return f(a,b,c-1,n-1)+f(a-1,b,c,n-1)+f(a,b-1,c,n-1); // 填空
}
int main()
{
printf("%d\n", f(1,1,1,2));
printf("%d\n", f(1,2,3,3));
return 0;
}
T6:最大公共子串 - 经典的dp问题
最大公共子串长度问题就是:求两个串的所有子串中能够匹配上的最大长度是多少。
比如:“abcdkkk” 和 “baabcdadabc”,可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
下面的程序是采用矩阵法进行求解的,这对串的规模不大的情况还是比较有效的解法。
请分析该解法的思路,并补全划线部分缺失的代码。
#include <stdio.h>
#include <string.h>
#define N 256
int f(const char* s1, const char* s2) {
int a[N][N];
int len1 = strlen(s1);
int len2 = strlen(s2);
int i,j;
memset(a,0,sizeof(int)*N*N);
int max = 0;
for(i=1; i<=len1; i++){
for(j=1; j<=len2; j++){
if(s1[i-1]==s2[j-1]) {
a[i][j] = a[i-1][j-1]+1; //填空
if(a[i][j] > max) max = a[i][j];
}
}
}
return max;
}
int main() {
printf("%d\n", f("abcdkkk", "acbdchd"));
return 0;
}
T7:正则问题 - 不规则递归
考虑一种简单的正则表达式:只由 x ( ) | 组成的正则表达式。
小明想求出这个正则表达式能接受的最长字符串的长度。
例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是6。
输入:一个由x()|组成的正则表达式。输入长度不超过100,保证合法。
输出:这个正则表达式能接受的最长字符串的长度。
例如,输入:((xx|xxx)x|(x|xx))xx ,程序应该输出:xxxxxx
考点:正则表达 - 递归

符号 意义 ^ 匹配行的开头 $ 匹配行的结尾 . 匹配任意单个字符 […] 匹配[]中的任意一个字符 (…) 设定分组 \ 转义字符 \d 匹配数字[0-9] \D \d 取反 \w 匹配字母[a-z],数字,下划线 \W \w 取反 \s 匹配空格 \S \s 取反 + 前面的元素重复1次或多次 * 前面的元素重复任意次 ? 前面的元素重复0次或1次 前面的元素重复n次 前面的元素重复至少n次 前面的元素重复至少n次,至多m次 | 逻辑或
#include<bits/stdc++.h>
using namespace std;
char s[105];
int index=0;
int f(){
int maxn=0; //结果
int temp=0; //中间过渡
while(index<strlen(s)) {
if(s[index]=='('){
index++;
temp+=f(); //统计一对括号中X的最大值返回之后将他记录到当前括号中
}
else if(s[index]==')'){
index++;
break;
}
else if(s[index]=='|'){
index++;
if(temp>maxn){
maxn=temp; //做出选择
}
temp=0; //重新计数
}
else{
temp++;
index++;
}
}
if(temp>maxn) maxn=temp;
return maxn;
}
int main(){
scanf("%s",s);
cout<<f()<<endl;
return 0;
}
T8:包子凑数 - 扩展欧几里得+完全背包-dp 不定方程--递归 **
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。例如,输入:
2
4
5程序应该输出:
6再例如,输入:
2
4
6程序应该输出:
INF
考点:不定方程-完全背包问题 dp - 递推公式
#include <iostream>
#include <bits/stdc++.h>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
using namespace std;
int n, g;
int a[101];
bool f[10000]; //开表 100*100-200 不能开出的极限
//求最大公约数
int gcd(int a, int b){
if(b==0) return a;
return gcd(b, a%b); // %表示求余
}
int main(int argc, char** argv) {
scanf("%d", &n);
f[0]=true;
for(int i=1; i<=n; ++i){
scanf("%d", &a[i]);
if(i==1) g=a[i]; //初始化最大公约数
else g=gcd(a[i],g);
for(int j=0; j<10000; ++j){
if(f[j]) f[j+a[i]]=true; //每输入新的数据,更新表;对于已经存在的数据,加上新数据的数是可以成立的
}
}
if(g!=1){
printf("INF\n");
return 0;
}
//统计个数
int ans =0;
for(int i=0; i<10000; ++i) {
if(!f[i]){
ans++;
//cout << i << endl; //看看是哪些数
}
}
printf("%d\n", ans);
return 0;
}T9:分巧克力-暴力枚举/二分枚举 ——基本功
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第 i 块是 Hi x Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:形状是正方形,边长是整数,大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?输入:
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。输出:
输出切出的正方形巧克力最大可能的边长。样例输入:
2 10
6 5
5 6样例输出:
2
考点:暴力枚举从高往低枚举/
优化:二分搜索
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int w[maxn], h[maxn];
int n, k;
int Enum(int l, int r) { //枚举边长为1到上限
int low = l, high = r;
while(low <= high) {
int mid = (low + high) / 2; //当前枚举的边长
int cnt = 0;
for(int i = 0; i < n; i++) {
cnt += (w[i] / mid) * (h[i] / mid); //看看能不能至少分成k块
if(cnt >= k) break; //满足条件
}
if(cnt >= k) {
low = mid + 1;
}
else {
high = mid -1;
}
}
return low - 1;
}
int main() {
cin>>n>>k;
int res = 0;
for(int i = 0; i < n; i++) {
cin>>w[i]>>h[i];
res = max(res, min(w[i], h[i]));//找到所有巧克力中较小边的最大值,作为枚举上限
}
cout<<Enum(1, res);
return 0;
}
T10:油漆面积- 暴力打点法/线段树+扫描线+矩形面积
X星球的一批考古机器人正在一片废墟上考古。该区域的地面坚硬如石、平整如镜。管理人员为方便,建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
经过各种测量,每个机器人都会报告一个或多个矩形区域,作为优先考古的区域。
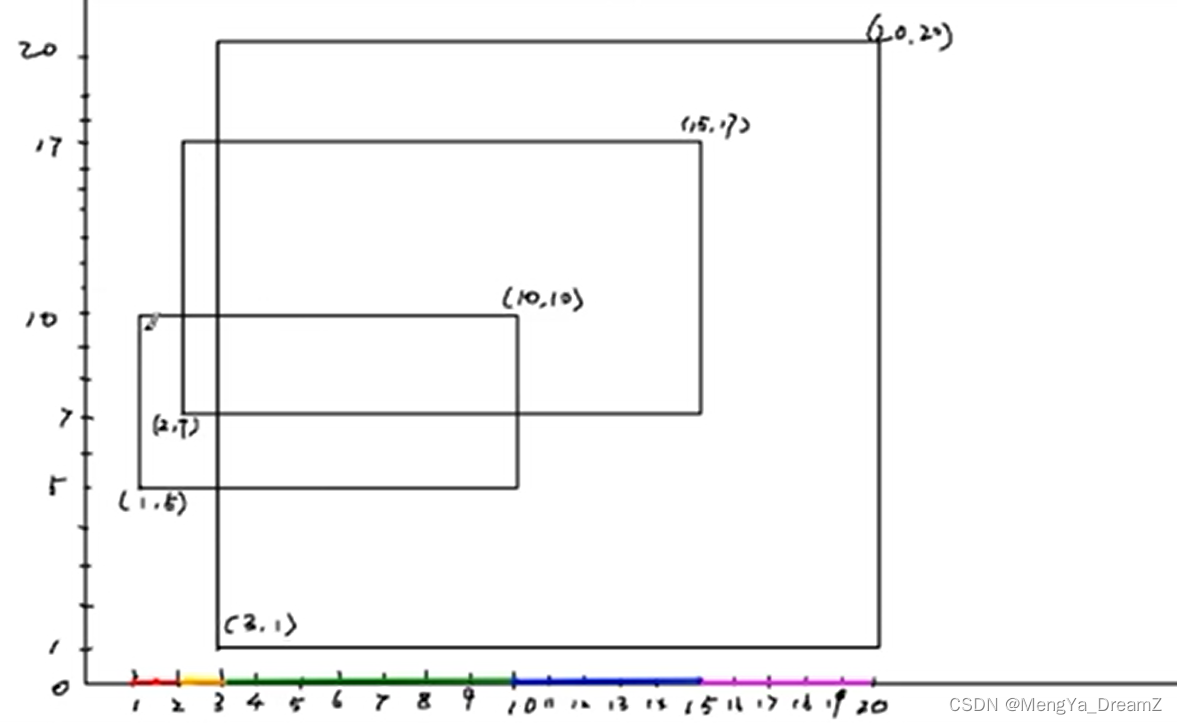
矩形的表示格式为(x1,y1,x2,y2),代表矩形的两个对角点坐标。
为了醒目,总部要求对所有机器人选中的矩形区域涂黄色油漆。小明并不需要当油漆工,只是他需要计算一下,一共要耗费多少油漆。
其实这也不难,只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意,各个矩形间可能重叠。本题的输入为若干矩形,要求输出其覆盖的总面积。
输入格式:
第一行,一个整数n,表示有多少个矩形(1<=n<10000)
接下来的n行,每行有4个整数x1 y1 x2 y2,空格分开,表示矩形的两个对角顶点坐标。
(0<= x1,y1,x2,y2 <=10000)输出格式:
一行一个整数,表示矩形覆盖的总面积。例如,
输入:
3
1 5 10 10
3 1 20 20
2 7 15 17程序应该输出:
340再例如,
输入:
3
5 2 10 6
2 7 12 10
8 1 15 15程序应该输出:
128
考点:遍历
进阶:线段树 / 扫描线 / 矩形
#include <iostream>
#include <bits/stdc++.h>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
using namespace std;
int n=0;
int sum=0;
bool p[10005][10005];
void paint(int x1, int y1, int x2, int y2){
for(int i=x1; i<x2; i++){
for(int j=y1; j<y2; j++){
p[i][j] =1;
}
}
}
int main(int argc, char** argv) {
scanf("%d", &n);
for(int i=0; i<n; i++){
int x1, y1, x2, y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
paint(x1, y1, x2, y2);
}
for(int i=0; i<10005; i++){
for(int j=0; j<10005; j++){
if(p[i][j]) sum++;
}
}
printf("%d\n",sum);
return 0;
}其余方案思路:2017年第八届蓝桥杯【省赛C/C++ A组】做题记录(附详细思路)