排序的概念及其引用:
排序的概念:
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的;画图说明:
排序前A在B前面,排序后说明该排序稳定,如果排序后B在A前面则说明不稳定。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
八大排序我们一般将其分为五类,分别为:
一: 插入排序
1. 直接插入排序
2. 希尔排序
二: 选择排序
1.直接选择排序
2.堆排序
三: 交换排序
1. 冒泡排序
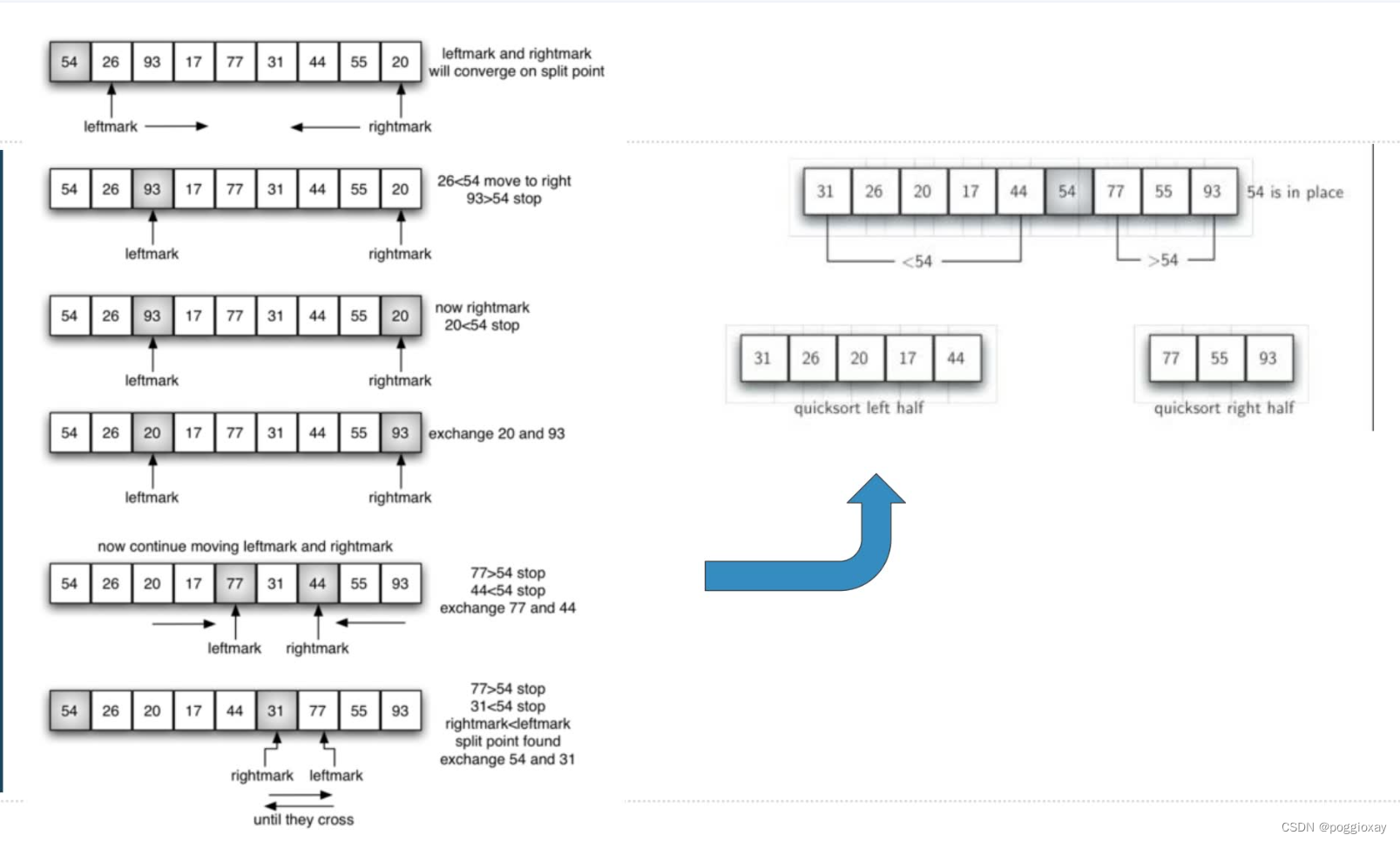
2. 快速排序
四: 归并排序
五:基数排序
插入排序:
直接插入排序:
基本思路:
思路:从第二个数开始,假设此数为
tmp,逐个往前进行比对,如果前数大于tmp,就将前数值赋值到tmp处,然后继续往前比对,直到找到小于或等于tmp的数(或者比对至数据首)就停止,最后将tmp的值赋值到此处就行了
动图演示:
代码:
public void insertSort(int[] array) {
if (array.length == 0) {
return;
}
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - 1;
for ( ; j >= 0 ; j--) {
if (array[j] > temp) {
array[j + 1] = array[j];
} else {
break;
}
}
array[j + 1] = temp;
}
}直接插入排序总结:
1. 集合元素越接近有序,时间效率越高
2. 时间复杂度: O(N^2)
3. 空间复杂度: O(1)
4. 稳定性: 稳定
希尔排序:
前言:
既然同为插入排序,那必然是有共同点的。
希尔排序是建立在直接插入排序基础上,经过优化的插入排序。
希尔排序分为两步:
- 1、预排序,使得数据尽可能接近有序
- 2、直接插入排序,最后调用一次直接插入排序,快速的完成排序
基本思路:
思路:
预排序是通过区间划分实现的,假设当前区间为gap,那么1、1+gap*n可以分成一组,同理2、3、4都可以分,将这些组分别进行直接插入排序(数据少,效率高)。每完成一次分组排序,gap就会缩小,直到gap为1时,进行一次直接插入排序,整个希尔排序就完成了
代码如下:
public static void shellSort(int[] array) {
int gap = array.length;
while (gap > 1) {
shell(array,gap);
gap /= 2;
}
//整体进行插入排序
shell(array,1);
}
public static void shell(int[] array,int gap) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - gap;
for ( ; j >= 0 ; j-= gap) {
if (array[j] > temp) {
array[j + gap] = array[j];
} else {
break;
}
}
array[j + gap] = temp;
}
}动图演示:
预排序:
直接插入排序:
希尔排序总结:
1. 希尔排序的时间复杂度要用到高数中的知识,“根据大量的数据的得到了局部的结论...”,我们直接记答案即可:O(N^1.25)
2. 空间复杂度: O(1);
我们仅仅只创建了一个gap
3. 稳定性: 不稳定;
我们在排序过程中gap会有多次的改变,不同的组别中可能会发生交换现象。
选择排序:
直接选择排序:
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
代码:
//选择排序
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}如果像这样去遍历的话,时间复杂度为O(N^2)不算是个很优解我们可以考虑对此进行优化
优化:每次遍历选最大与最小,分别与 end 值和 begin 值交换
动图演示:

直接选择排序总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
堆排序:
我们之前也介绍过堆排序,PriorityQueue本质就是个小根堆,这里就不过多介绍了。
思路:堆排序用到了堆的知识,如果想排升序的话建大堆,因为大堆中堆顶是最大值,将堆顶值与堆低值交换后,执行向下调整,使其再次变为大堆,就这样反复交换、调整,堆排序就完成了。
/**
* 堆排序
* @param array 目标数组
*/
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length - 1;
while (end > 0) {
swap(array,0,end);
shiftDown(array,0, end);
end--;
}
}
public static void createBigHeap(int[] array) {
//父下标 从倒数第二层开始
int parent = (array.length - 1 -1) / 2;
for (; parent > 0 ; parent-- ) {
shiftDown(array,parent, array.length);
}
}
public static void shiftDown(int[] array,int parent,int len) {
int child = 2*parent + 1;
while (child < len) {
if (child + 1 < len && array[child] < array[child + 1]) {
child++;
}
if (array[child] > array[parent]) {
swap(array, parent, child);
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}
private static void swap(int[] array,int i,int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}向上调整动图演示:

堆排序总结:
1. 堆排序使用堆来选数相对于直接插入排序,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
本文只是排序的上半部分,涉及的排序思想都还算简单,下一篇文章中将会介绍排序大哥:快速排序,知识点很难敬请期待吧。