目录
0.前言
1.什么是栈
2.实现栈所选择的基本结构
3.认识栈的小练习
4. 用代码实现一个栈
4.1 用什么可以描述出一个栈
4.2栈接口的设计原则
4.3栈的初始化
4.4栈的插入
4.5 栈的删除
4.6 栈的判空
4.7栈的有效元素的数量
4.8取出栈顶元素
4.9栈的销毁
5. 对实现栈的测试与应用
0.前言
本文代码以及画图都已上传至gitee码云,可自取:
4栈的实现 · onlookerzy123456qwq/data_structure_practice_primer - 码云 - 开源中国 (gitee.com)
https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/4%E6%A0%88%E7%9A%84%E5%AE%9E%E7%8E%B0开始本文内容:
1.什么是栈
先举一个不雅的例子,栈其实就是有口无肛门的生物,进食从口进,消化后的排泄物也从口出。然后排的时候,肯定是后吃进去的食物压在先吃进去的食物的上面,肯定是这个后吃进去食物先排出去,然后这个先吃进去的食物才能排出去。
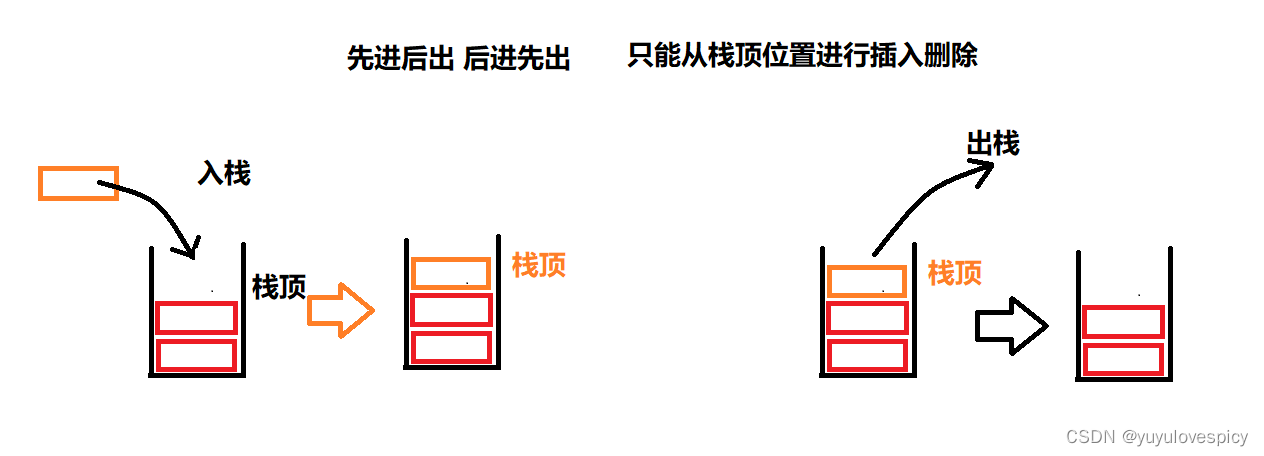
栈这个数据结构,可以用一句话总结:后进先出,先进后出。
再举一个之前的例子,我们之前学过的顺序表/链表,是一个线性结构,这个栈也是一个线性结构。栈其实是顺序/链表的功能退化版本,就是对顺序表/链表的阉割。
顺序表可以在任意位置进行插入与删除,而栈是只能在一端进行插入与删除。
我们出数据是在一端,入数据也能在这一端,这一端我们称之为 栈顶。无论是入数据还是出数据,都是只在栈顶操作,这样其实也达成了我们先进后出的目的。
2.实现栈所选择的基本结构
光说不练,假把式。我们实现一个栈,其实可以使用两种线性结构,一种是数组结构,一种是链表结构。所以我们可以实现数组栈,可以实现链式栈,只要让这个数据结构能做到栈的操作即可。
那我们具体用哪一种呢?
栈只能在栈顶进行插入删除,所以无论是数组栈还是链表栈,我们只要限定只能选定一端(首 / 尾)进行插入删除即可。
对于顺序表这个数据结构来说,我们肯定是不是选定头插/头删,因为这样效率是O(N),我们肯定是选择尾部作为栈顶,尾插/尾删的效率是O(1)嘛。从效率上说,用顺序表结构实现的栈,已经很优秀了。
可是顺序表自身也是有缺点的,一是realloc扩容,如果是异地扩容,那效率就是很低的,二是我们为了防止频繁扩容,我们通常扩容是二倍扩,这样也会存在空间的浪费。
对于链表数据结构实现栈来说,如果是非常普通的单链表,我们肯定是选用头插/头删(以头部作为栈顶),效率为O(1),因为单链表尾插/尾删需要找尾,效率为O(N)很低。
当然啦,你设计成双向循环链表方便找尾,单链表只能选头插头删,尾插/尾删效率也很好,也是O(1)。
可是链表自身也是有缺点的,那就是缓存命中率低:
3.2 缓存命中率
https://blog.csdn.net/qq_63992711/article/details/128664914?spm=1001.2014.3001.5502#t16详情可以看这个博客片段。
总结:
两种结构架构栈都可以!如果非要选一种,数组(顺序表)结构稍好一点,因为缓存命中率更高,而且我们现在更看重效率,而不是看重对空间的过度节省,所以我们选用顺序表结构实现栈。
3.认识栈的小练习
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈。然后再依次出栈,则元素出栈的顺序是()
A. 12345ABCDE
B. EDCBA54321
C. ABCDE12345
D. 54321EDCBA
按照先进后出,后进先出(上面的出了,下面的才能出),我们依次分析四个选项:
A:入1,出1,入2,出2,入3,出3..........................入E,出E。即可达到A选项的出栈顺序。
B:直接入1 2 3 4 5 A B C D E,然后反着出E D C B A 5 4 3 2 1,就可以达到B选项的出栈顺序。
C:入1 2 3 4 5 A,出A,入B,出B,入C,出C,入D,出D,入E,出E,现在从栈顶到栈底,依次是5 4 3 2 1 (我们入的顺序是1 2 3 4 5,先进的后出),所以出栈的顺序只能是5 4 3 2 1 ,所以说C选项错误。
D:入1 2 3 4 5,出 5 4 3 2 1,入A B C D E,出E D C B A。
4. 用代码实现一个栈
4.1 用什么可以描述出一个栈
我们选定顺序表结构实现一个栈,我们选定在堆区开辟这个连续的顺序表,所以一个栈需要存储一个指向栈实体数组空间的指针_a。
然后我们还需要记录栈顶的位置,这个位置决定了我们插入删除的位置(很重要),所以我们记录一个int _top为栈顶,_a[_top]的位置就是下一个要插入数据(入栈)的位置,_a[_top-1]此时是栈顶的元素,同时_top也能代表当前栈内有效元素的数量的大小。
同时顺序表需要每次扩二倍,所以我们不仅要记录有效元素数目的大小_top,所以还要记录_capacity,代表数组空间容量的大小(我这个栈可以容纳存储多少个有效数据)。
//范式的数据类型,方便修改
typedef int STDataType;
//使用数组结构,以尾部作为栈顶,尾插尾删实现栈
typedef struct Stack
{
STDataType* _a; //指向栈实体数组空间
int _top; //下一个要插入数据的下标&&数组有效数据数量
int _capacity; //数组空间容量
}Stack;4.2栈接口的设计原则
我们要改变一个栈,比如要对一个定义出来的栈进行修改,例如我们传入这个栈进入一个插入接口,经过这个插入接口作用后,可以使得这个栈得到改变。所以我们传参的话,是不可以直接传入这个Stack对象的,因为传值传参我们都是对原对象的拷贝,并不是在改变到传入这个Stack对象的实体,而是在改变这个Stack对象的拷贝。所以我们传入的应该是栈Stack对象的指针。根据指针指向的,就是我们在接口外这个Stack栈对象实体,修改的就不是拷贝了。
//传参传入指向三个结构体变量的指针
void StackInit(Stack* ps);
void StackDestroy(Stack* ps);
bool StackEmpty(Stack* ps);
int StackSize(Stack* ps);
void StackPush(Stack* ps, STDataType x);
void StackPop(Stack* ps);
STDataType StackTop(Stack* ps);4.3栈的初始化
我们在程序当中,定义一个struct Stack对象,那此时其内部的_a是野指针,且_top和_capacity都是随机值,如果不初始化或者忘记初始化,而直接进行插入删除操作的话,那就会导致灾难性的后果(野指针非法访问,_top随机值非法位置访问)。
所以每次定义出一个栈,都要初始化其成员变量。
void StackInit(Stack* ps)
{
ps->_a = NULL;
ps->_top = ps->_capacity = 0;
}
4.4栈的插入
栈的插入,即入栈,只能从栈顶的位置(_a[_top])进行插入,所以插入只需要用户传入元素,我们在栈的内部实现上直接在栈顶插入即可。
但是每次插入之前,我们必须检查扩容,这个是容易遗忘的。每次插入成功之后,我们还需要++有效数据的个数 / 更新栈顶的位置,即要++_top。
void StackPush(Stack* ps,STDataType x)
{
//首先传入的必须是有效的栈
assert(ps);
//检查扩容
if (ps->_top == ps->_capacity)
{
int newcapacity = (ps->_capacity == 0) ? 8 : ps->_capacity * 2;
STDataType* ptmp = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
if (ptmp == NULL)
{
perror("realloc error");
exit(1);
}
//申请成功
ps->_a = ptmp;
ps->_capacity = newcapacity;
}
//队尾插入<=>尾插数据
ps->_a[ps->_top] = x;
ps->_top++;
}同时我们也要检查用户传入的是不是一个有效的栈指针,如果传入的是一个NULL,这就不是一个指向栈的指针,需要反馈报错。
4.5 栈的删除
栈的删除:在顺序表结构实现中,栈的删除是其实是伪删除,其实只需要--_top,减少有效数据的一个数量,这样就可以完成删除了。
可是每次删除都需要检查,如果栈是空,那我们其实就不能无脑删除,要对外进行报错提示!同时也要记住,删除要更新有效数据的数量 / 栈顶位置_top--。
void StackPop(Stack* ps)
{
//有效栈
assert(ps);
//必须有数据才能删除
assert(ps->_top > 0);
/*更形象可以这样写:assert(!StackEmpty(ps));*/
//顺序表数量--,即可删除
ps->_top--;
}4.6 栈的判空
判断栈是否为空,就是看栈内有效元素的数量的是否为0即可,而_top的大小便代表了这一点。所以如果_top==0,那栈就是空的。
PS:在C语言当中如果想使用bool类型,需要包一个头文件#include<stdbool.h>即可。
同时也要记得检查用户传入的是否是一个有效栈指针,如果是非法栈,比如传一个NULL,那就会导致对空指针解引用的问题。
bool StackEmpty(Stack* ps)
{
//传入的是有效的栈
assert(ps);
return ps->_top == 0;
}4.7栈的有效元素的数量
我们在外部针对一个栈对象,获取这个栈对象内有效元素的数量,这点是需要的。所以我们设计一个返回栈内有效数据数量的接口。这个_top要插入栈顶位置大小,其大小也代表着栈内有效元素的数目。
int StackSize(Stack* ps)
{
//传入的是一个有效栈指针
assert(ps);
return ps->_top;
}4.8取出栈顶元素
我们只能从栈顶进行插入删除,对于一个栈来说我们可以获取的数据,只能是栈顶的元素,所以我们需要顶一个接口,返回获取栈顶元素现在是什么。栈顶的元素就是_a[_top-1],同时我们也要检查现在栈不为空(不为空才有元素取),检查现在是一个有效的栈指针。
STDataType StackTop(Stack* ps)
{
//有效栈
assert(ps);
//必须有数据才能取出
assert(ps->_top > 0);
/*更形象可以这样写:assert(!StackEmpty(ps));*/
return ps->_a[ps->_top - 1];
}4.9栈的销毁
我们说栈区的变量空间,在最后可以由系统回收。可是在堆区的变量空间,必须要主动free掉,否则就会导致内存泄漏。而我们定义的一个栈,是有一个连续的定义在堆区的数组空间*_a,所以说在程序结束之前,我们必须要释放掉这块堆区空间!!!即我们在使用完一个栈之后,一定一定要Destroy!!!
void StackDestroy(Stack* ps)
{
//传入的是有效的栈
assert(ps);
free(ps->_a);
ps->_top = ps->_capacity = 0;
}5. 对实现栈的测试与应用
我们实现数据结构,就必须要对之进行测试检查,能不能满足我们实际当中的应用,下面我们设计几个应用栈的简单场景进行测试。
#include"Stack.h"
void StackTest1()
{
Stack st;
StackInit(&st);
StackPush(&st, 4);
StackPush(&st, 7);
StackPush(&st, 0);
StackPush(&st, 9);
StackDestroy(&st);
}
void StackTest2()
{
Stack st;
StackInit(&st);
StackPush(&st, 4);
printf("Stack size:%d\n", StackSize(&st));
StackPush(&st, 7);
printf("Stack size:%d\n", StackSize(&st));
StackPush(&st, 0);
printf("Stack size:%d\n", StackSize(&st));
StackPush(&st, 9);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackPop(&st);
printf("Stack size:%d\n", StackSize(&st));
StackDestroy(&st);
}
void StackTest3()
{
//测试基本的遍历栈
Stack st;
StackInit(&st);
//依次入栈
StackPush(&st, 4);
StackPush(&st, 1);
StackPush(&st, 3);
StackPush(&st, 1);
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 5);
//栈:先进后出,后进先出
while (!StackEmpty(&st))
{
//寻找栈顶数据
int top = StackTop(&st);
//栈顶数据出栈
StackPop(&st);
printf("%d ", top);
}
printf("\n");
StackDestroy(&st);
}
int main()
{
//StackTest1();
StackTest2();
//StackTest3();
return 0;
}![BUUCTF-[ACTF新生赛2020]Splendid_MineCraft](https://img-blog.csdnimg.cn/d7cbfec2fa1a405a81ffb5148a4f93eb.png)