前言
《信号与系统》是一门很难的课,也是许多学校考研要考的专业课,由于每周只有两节课,所以每次上完都要及时的去复习,这里参考的教材是奥本海姆著作,刘海棠译,北京:电子工业出版社,2013年。
信号类型的区分
-
确定信号与随机信号
确定信号:若被表示为一确定的时间函数,知道某一时间即可得知当前的信号信息。
随机信号:带有随机的特点,无法预测,不能用函数表示,只能用概率统计的方法描述的信号。
-
连续信号与离散信号
连续信号:连续时间范围内有定义的信号,自变量用t表示。
离散信号:在时间上表示离散,仅能用整数表示,自变量用n表示。 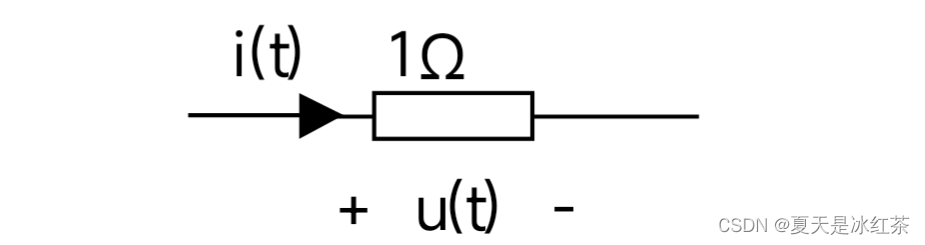
在连续信号的情况下,对于1欧姆的电阻上,不管是电压信号u(t)还是电流信号i(t),都将其定义为x(t),则其瞬间功率为。
能量:
若,
平均功率:
那么对于离散信号
能量:
平均功率:
-
能量信号与功率信号
能量: 平均功率:
可以看出
若,则将x(t)或x[n]称为能量信号(
,E有界)。
若,则将x(t)或x[n]称为功率信号(
,P有界)。
可以这样理解,当信号具有有限的能量,即
,这种信号的平均功率必为0;第二种信号就是其平均功率
有限的信号,如果
,必有
,因为如果单位时间内有某一个非零的平均功率,在无限积分或求和就必然得出无限大的能量值。
第三类信号就是
和
都不是有限的。
如果这样说还是不能理解,那么就举些例子,比如信号在内为1,在此区间外为0就是有限能量信号的另一个例子,此时
,例如常数x[n]=4就具有无限能量,但是平均功率
,在看信号x(t)=t,
和
都不是有限的。
总结:它们有下面的这几种组合
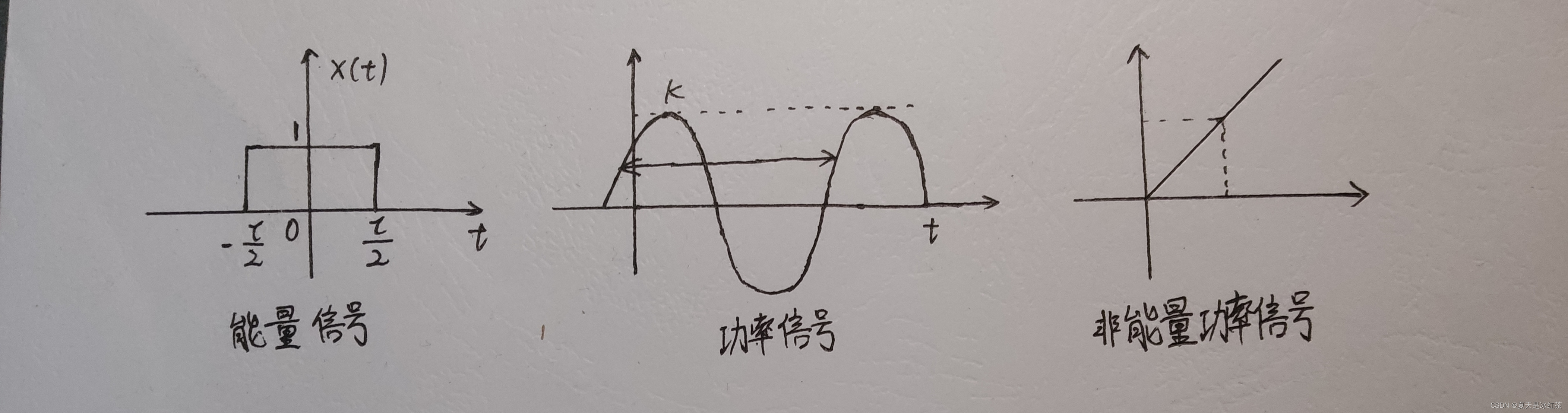
有限能量+零功率---->能量信号
代表波形:孤零零的方波、极限值为0的波形
无穷能量+有限功率--->功率信号
代表波形:一个无限延伸的正弦波、无线长的白噪声
无穷能量+无穷功率--->非功非能信号
代表波形:无限延伸的单调波形
-
周期信号与非周期信号
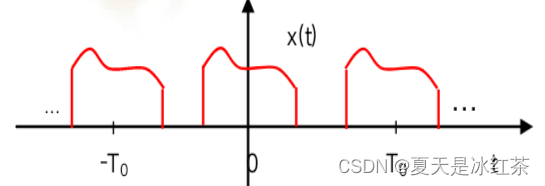
连续周期信号:一个连续信号x(t),若对所有t均有:x(t)=x(t+kT),k为整数。满足这个式子的最小周期为基波周期,用T0来表示。
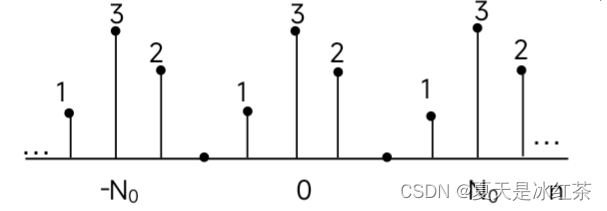
离散周期信号:一个离散信号x[n],若对所有n均有:x[n]=x[n+mN],m为整数。满足这个式子的最小周期为基波周期,用N0来表示。
-
连续时间和离散时间信号
对于信号的组合,它的周期性判断以及基波周期的求解:
(1)连续信号
,若
是有理数
则
是周期的,其基波周期:T0=LCM(
),LCM最小公倍数。
(2)离散信号
一定是周期的,其基波周期为:N0=LCM(
)。