序

参考的是这个书：Python神经网络编程 (豆瓣) (douban.com)

小白，0基础，也看不懂其它更复杂的书……

01.正向计算

从左到右，根据输入值，得到输出值

总览

这就是神经元的数学形式：

阈值函数

sigmoid函数：

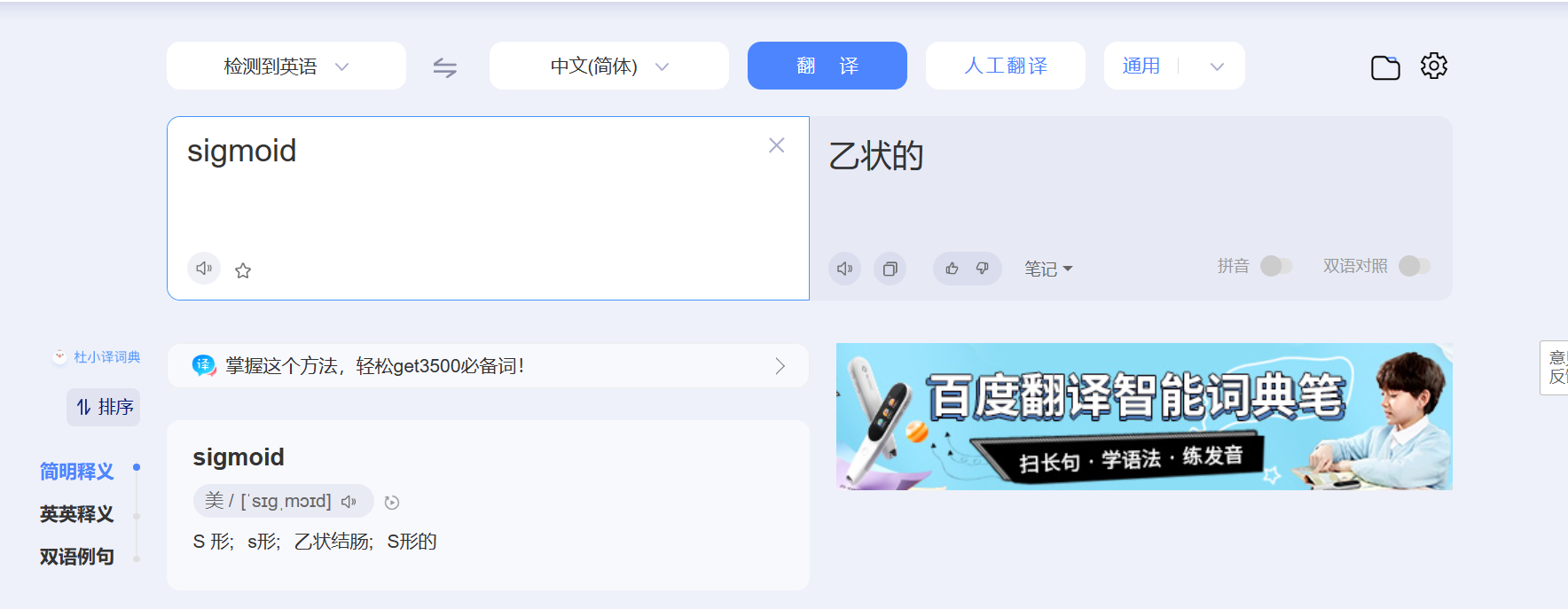
具体是这个形状：

输入输出

大概是这么算的：

里面有个组合输入的概念

这个是具体的计算过程：

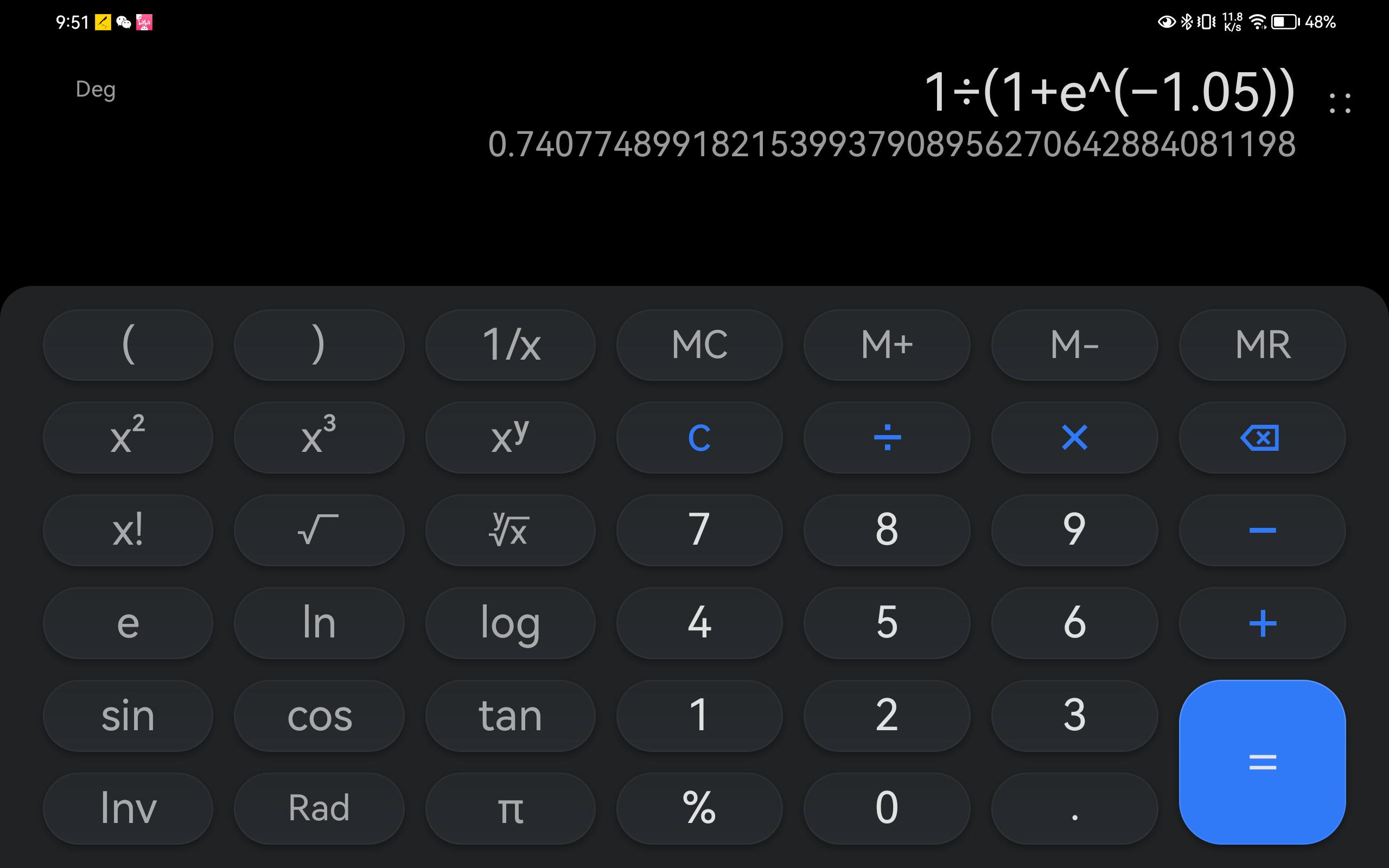
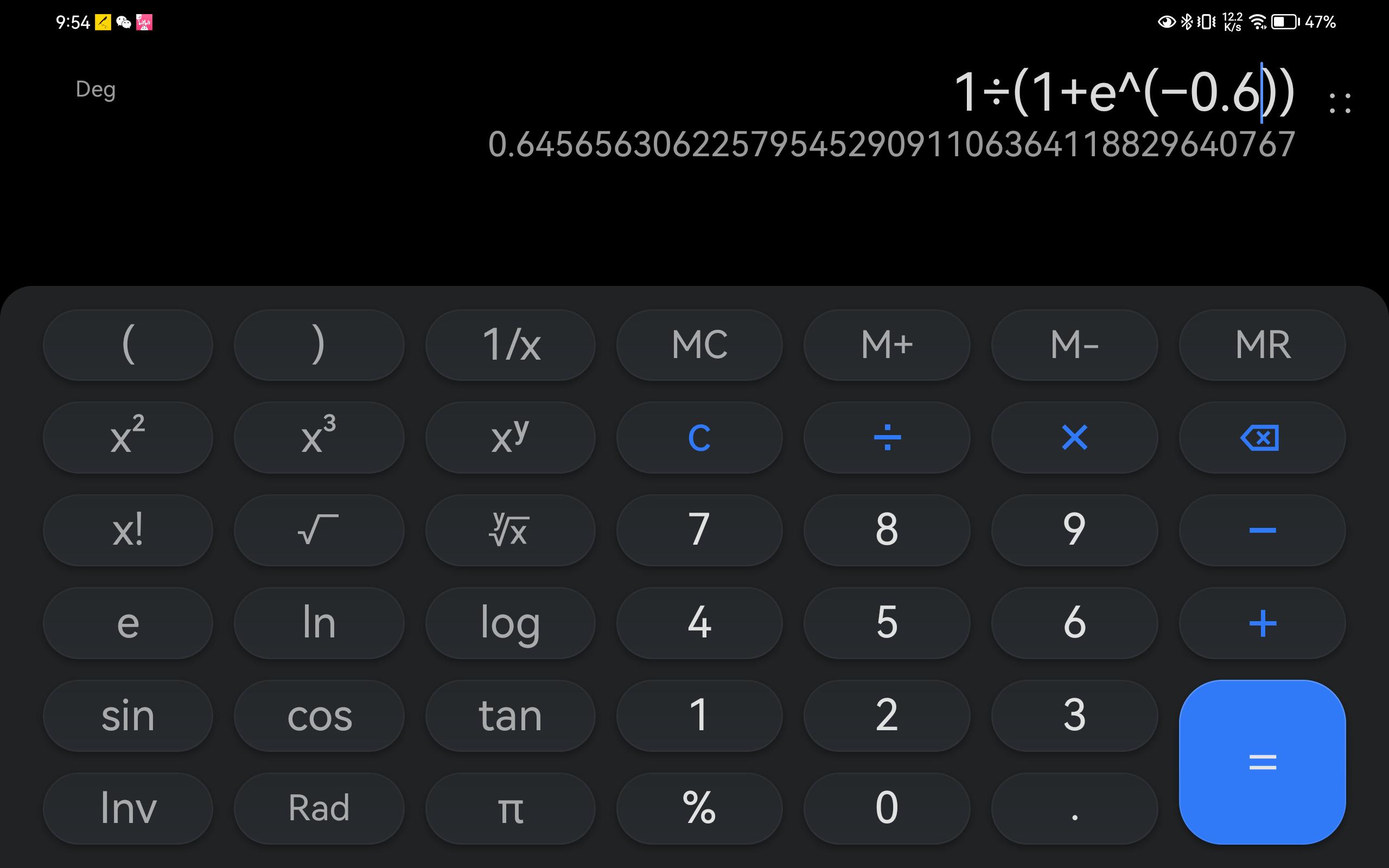
矩阵形式

组合输入，是个先乘法再加法的过程；

矩阵乘法，好像也是；

所以，可以把组合输入写成矩阵乘法的形式：

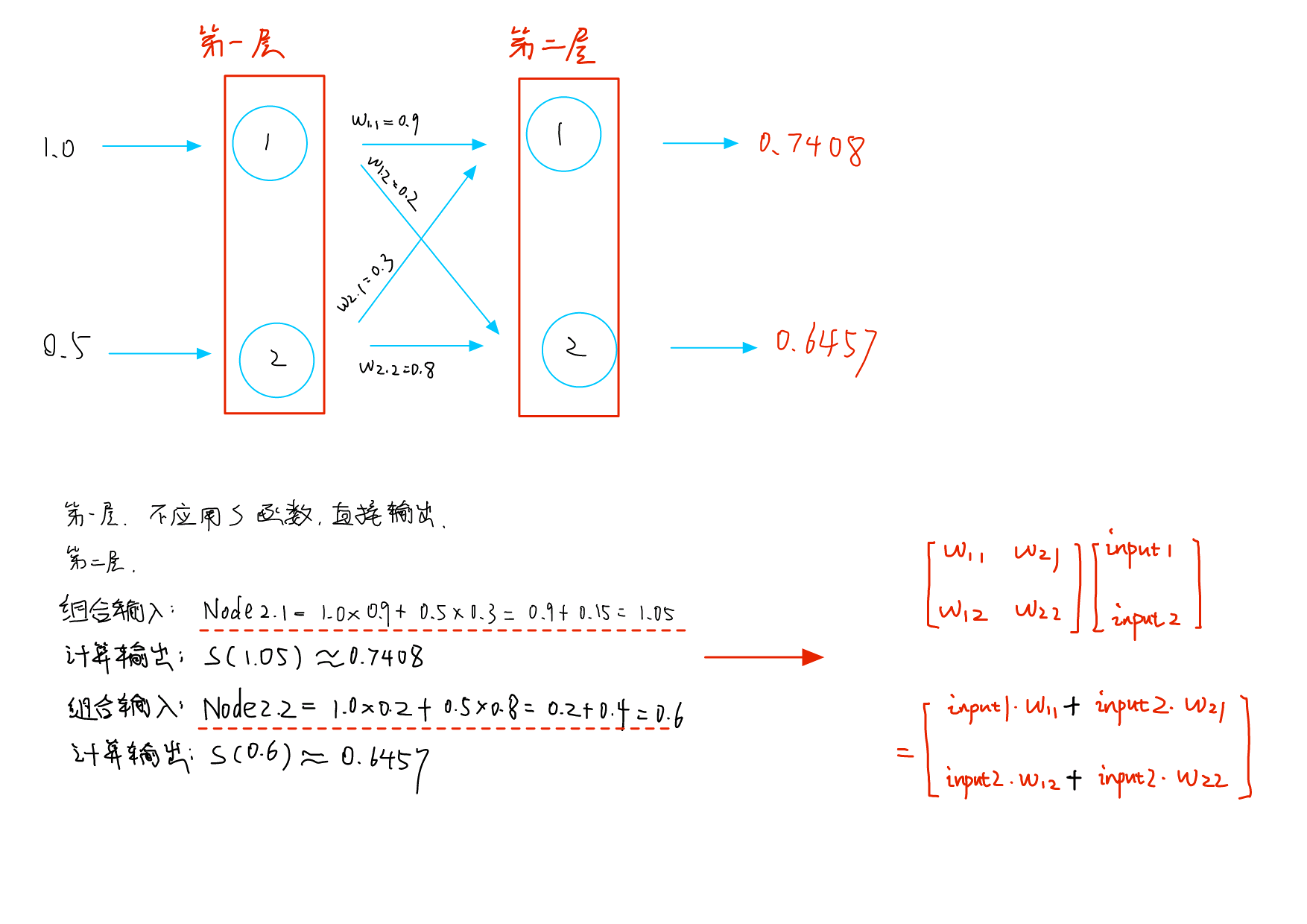
这是封装啊……封装成框架，然后就通用了：

X=WI

W是权重矩阵：weight

每层2个节点，它就是2*2的规模；

I是输入矩阵，input

每层2个节点，它就是2*1的规模；

这个矩阵的规模，和上一层，当前层的节点数，都是相关的。

02.反向计算

从右到左，计算出预期的值与实际的值的差异。

这个差异值是用来调节权重的，所以，要为每个权重分别计算差异值。

怎么算？

它是组合输入的，所以这个误差是多个权重共同造成的

权重，是边的权重，两头都有的才叫边，只有一头的叫点

情况1

输出层3和隐藏层2，之间的链接，怎么分误差？

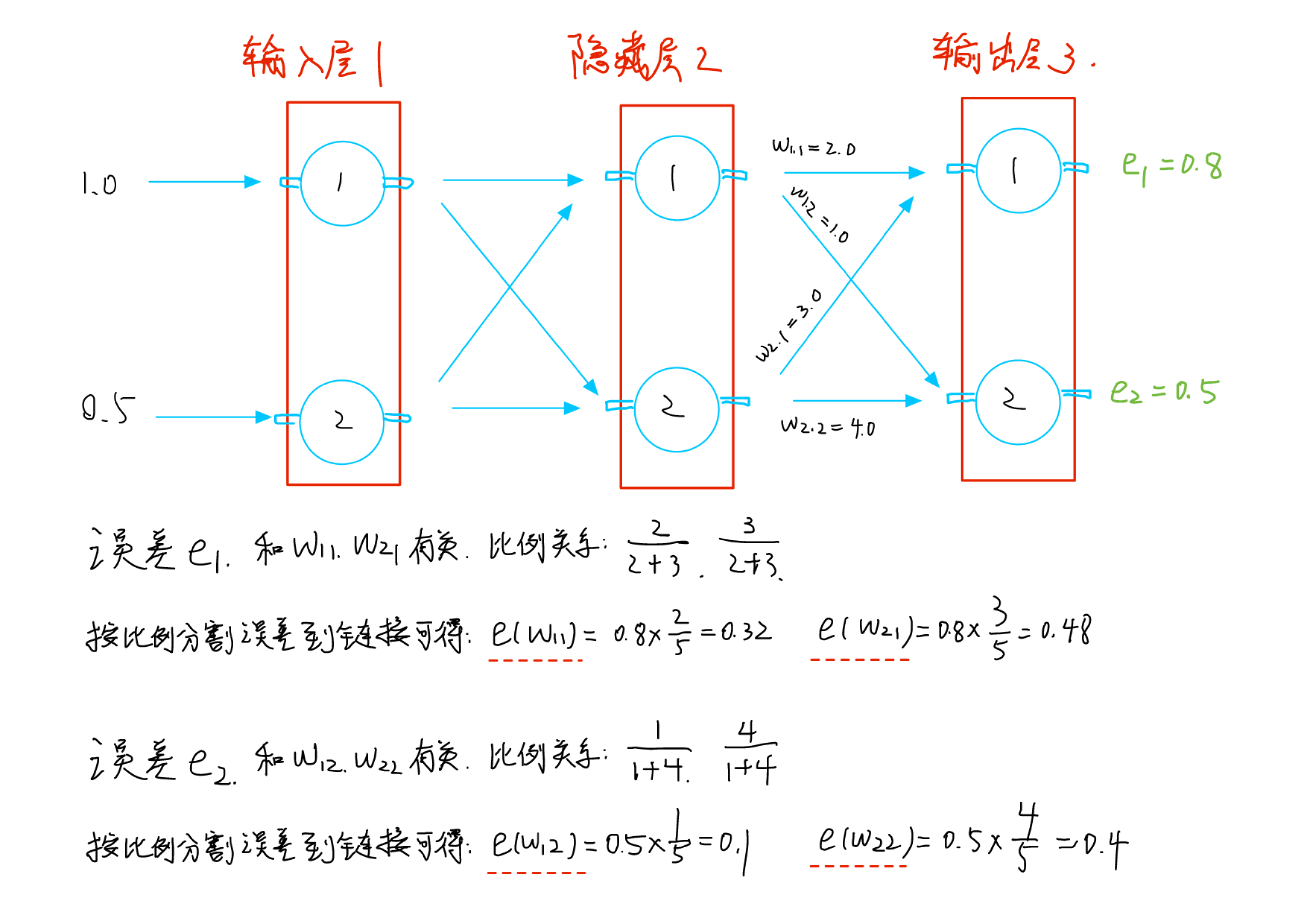
没毛病，完了吗？还没完；输入层1和隐藏层2之间的链接，还没分到误差。这个怎么算？

情况2

首先，得有误差，才能反向传播

哪来的误差，这个又不是输出层

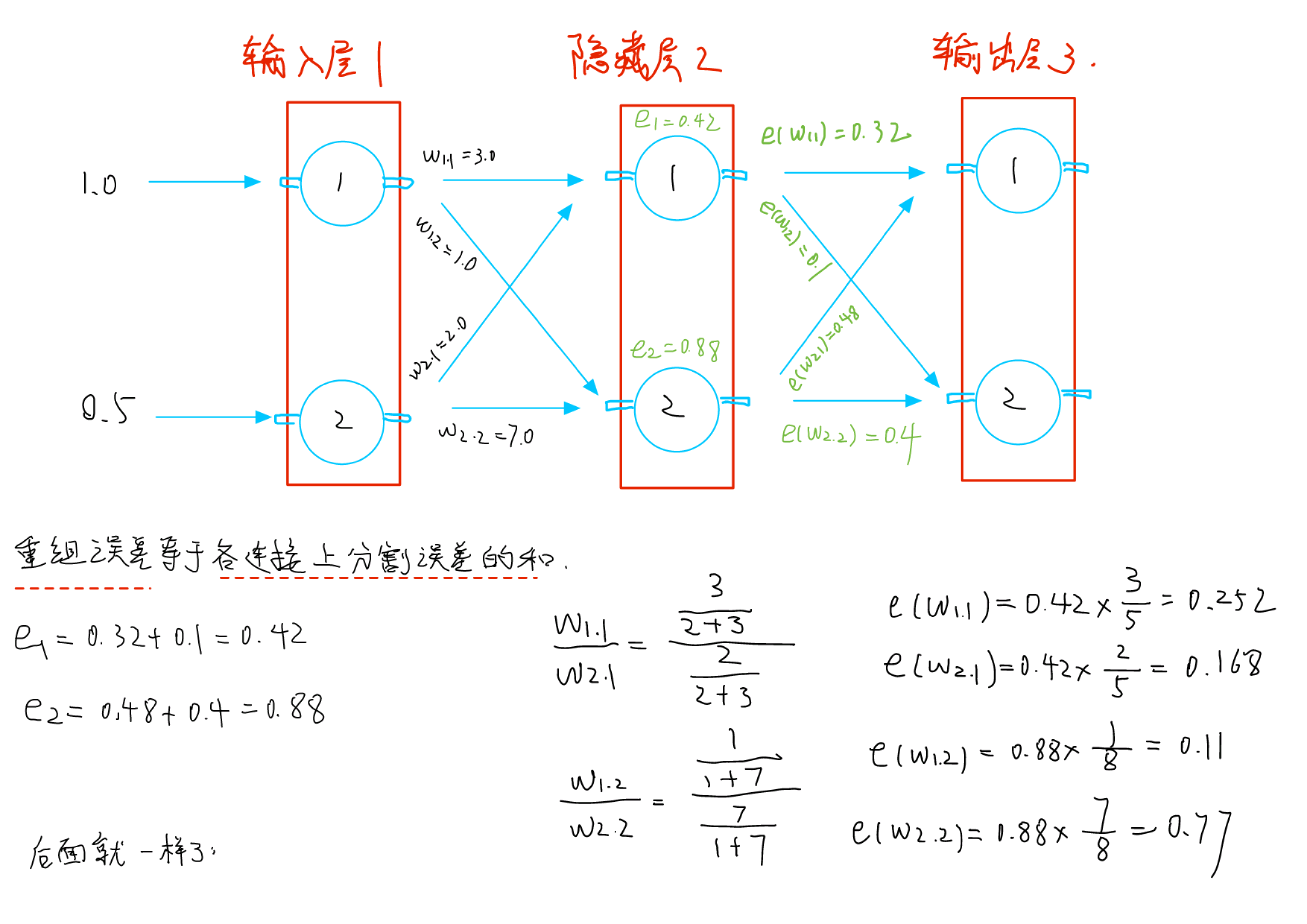
通过重组，得到误差：重组误差等于链接上误差的和；链接上的误差是什么？就是上一步按比例分割得到的。

矩阵形式

能不能也封装成矩阵形式？

重组误差等于各链接上分割误差的和，分割误差是用乘法算出来的；先乘法再加法……矩阵乘法也是这俩

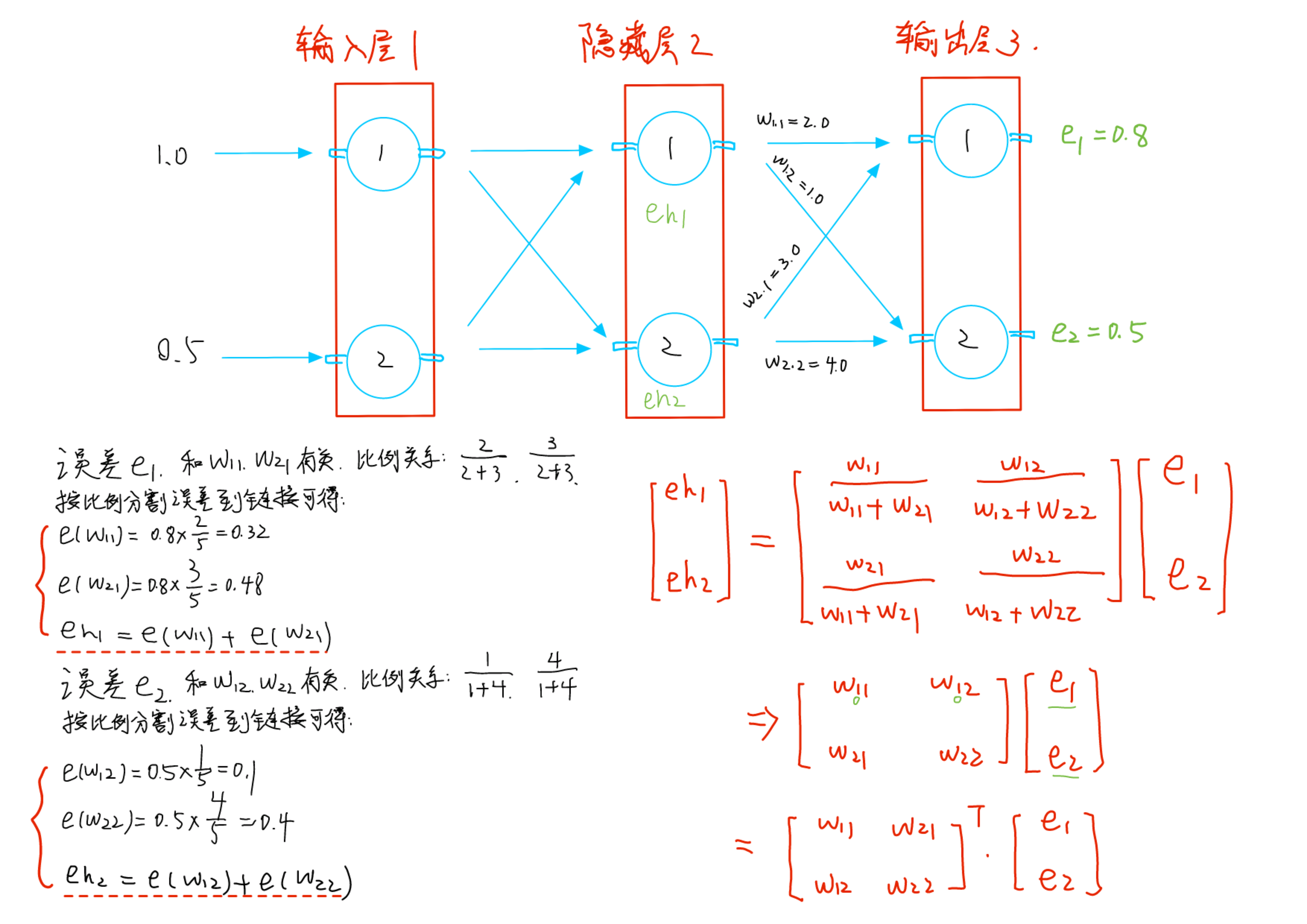
而且，从矩阵下标上，可以看出来，它确实是反向传播。

这个矩阵，也可以当成是正向计算时候用的权重矩阵的转置。

03.求导与更新

猜数字，如果5大了，可能会改成3。

现在，每个权重都按比例分到了相应的误差。怎么根据误差逐个更新权重？

从计算的过程可以看出来：误差和输出有关，输出又和权重有关，所以误差和权重有关；

梯度下降

(14条消息) 牛顿法-梯度下降法_leo_fighting的博客-CSDN博客_梯度下降示意图

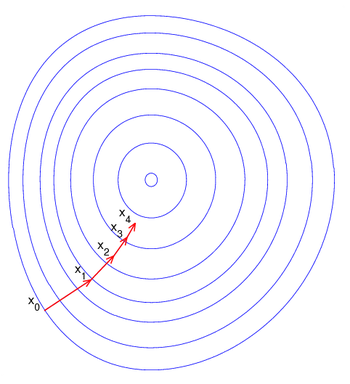
根据误差更新权重，单个权重是个标量

已有标量X，更新后是X+ΔX

那么，ΔX，是正是负？

和斜率反着来就行了；斜率正数，就正，斜率负数，就负

负号有了，具体的值是多少呢？大概和斜率绝对值有关吧

一个标量X，就是这么更新的。

如果误差和8个权重标量有关呢？如上图。

一元的是斜率；多元的就叫梯度了，梯度是个向量，每个分量都是偏导的形状

无非就是1+1和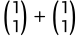的关系，重复而已

偏导

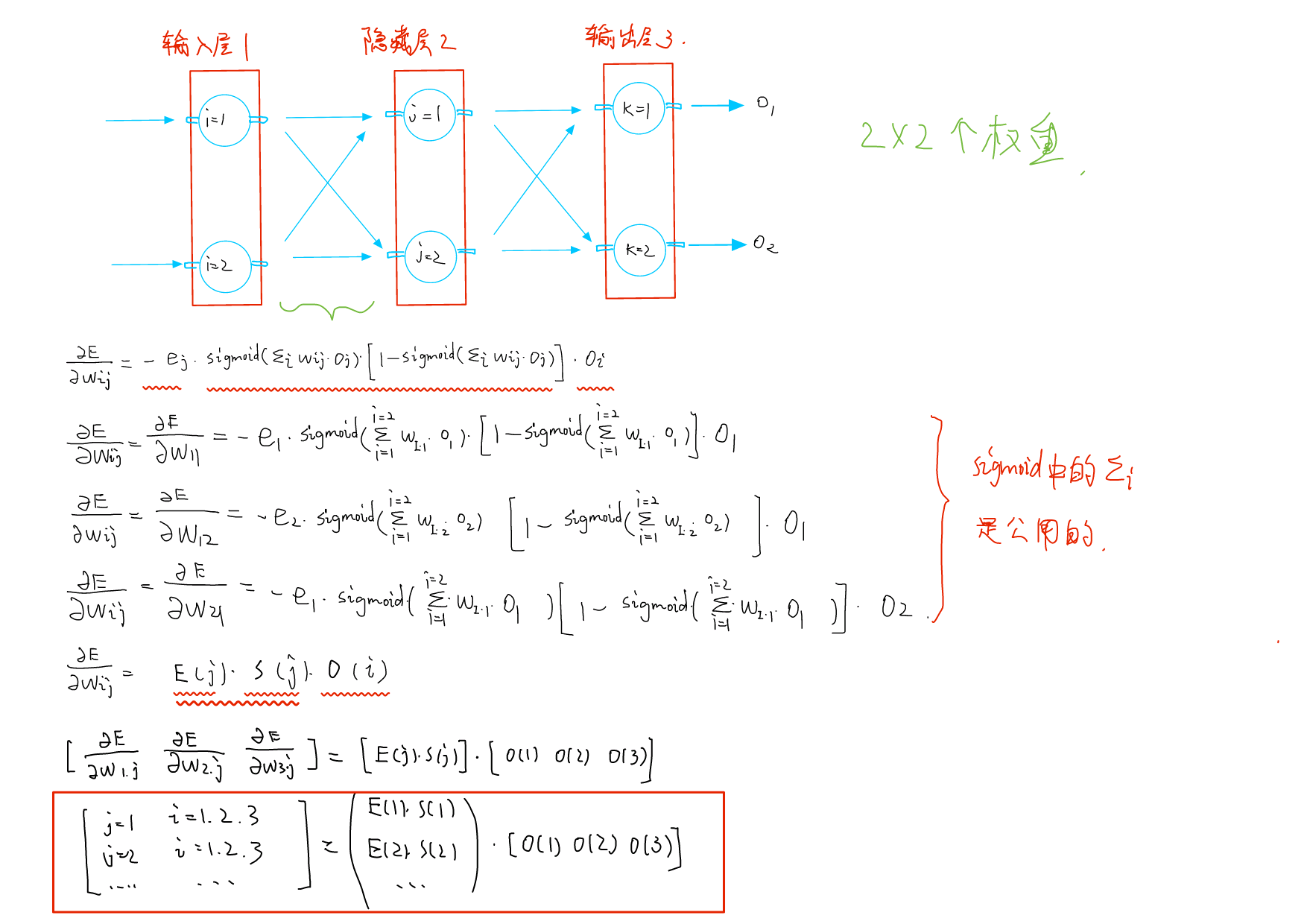
那么，误差关于权重的偏导怎么求？

2和3之间的是这么算的：

1和2之间的可以类比：

矩阵形式

能不能也封装成矩阵形式？

这个不存在什么先乘法再加法的情况；但是先写写看吧

可以把那3个部分，抽象成函数的形式，俩变量，ij

怎么看呢？

先按住j——让j当常数【偏导就是这么干的】；

再放开i——让i作变量

就看到结构上的规律了。

后记

原理大概就这么多。

书的后面好像还有个实际应用。