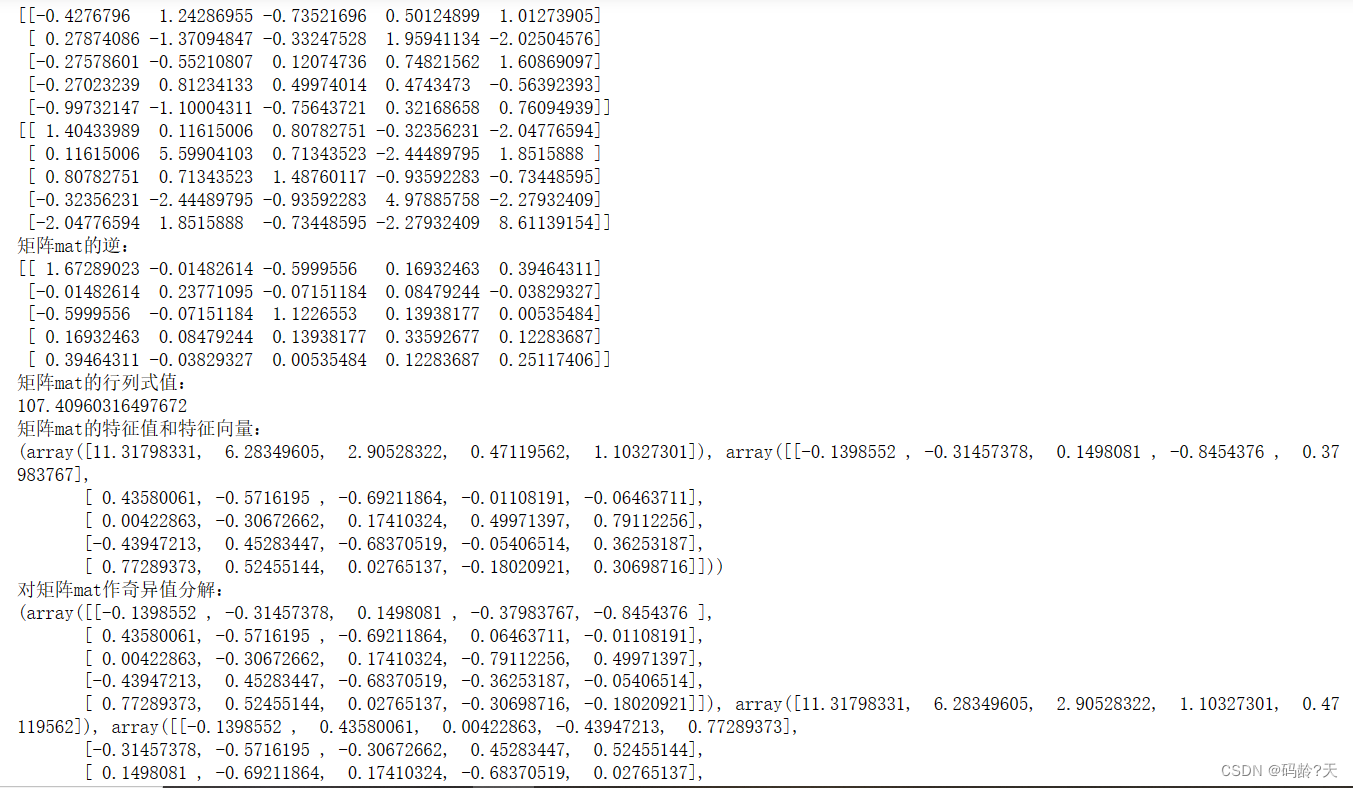
文章目录
- 特征分解
- 几何示意图
- 二次型和生成子空间
- 奇异值分解
- 理论数学风格的描述
- 奇异值分解和特征分解的联系😊🎈
- 机器学习风格的描述
- 对角矩阵的记法
- 酉矩阵unitary matrix
- 性质
- Moore-Penrose 伪逆
- 矩阵的逆和线性方程组的解(review)
- 伪逆
- 应用
- 迹运算
- 方阵行列式和特征值
特征分解
许多数学对象可以通过将它们分解成多个组成部分或者找到它们的一些属性而更好地理解,这些属性是通用的,而不是由我们选择表示它们的方式产生的。
-
例如,整数可以分解为质因数。我们可以用十进制或二进制等不同方式表示整数 12,但是 12 = 2 × 2 × 3 永远是对的。从这个表示中我们可以获得一些有用的信息,比如 12 不能被 5 整除,或者 12 的倍数可以被 3 整除。
-
正如我们可以通过分解质因数来发现整数的一些内在性质,我们也可以通过分解矩阵来发现矩阵表示成数组元素时不明显的函数性质。
-
特征分解(eigendecomposition)是使用最广的矩阵分解之一,即我们将矩阵分解成一组特征向量和特征值。
-
方阵 A 的 特征向量(eigenvector)是指与 A 相乘后相当于对该向量进行缩放的非零向量v :
- 右特征向量 A v = λ v , v ≠ 0 Av=\lambda{v},v\neq{0} Av=λv,v=0
- 左特征向量 v T A = λ v T , v ≠ 0 v^TA=\lambda{v^T},v\neq{0} vTA=λvT,v=0
-
假设矩阵 A 有 n 个线性无关的特征向量 v ( 1 ) , ⋯ , v ( n ) {v^{(1)}, \cdots , v^{(n)}} v(1),⋯,v(n),对应着特征值 λ 1 , ⋯ , λ n {λ_1,\cdots, λ_n} λ1,⋯,λn。
-
我们将特征向量连接成一个矩阵,使得每一列是一个特征向量:
- V = ( v ( 1 ) , ⋯ , v ( n ) ) V=(v^{(1)}, \cdots , v^{(n)}) V=(v(1),⋯,v(n))
-
将特征值连接成一个向量 λ = [ λ 1 , . . . , λ n ] ⊤ λ = [λ_1, . . . , λn]^⊤ λ=[λ1,...,λn]⊤。
-
因此 A 的 特征分解(eigendecomposition)可以记作
- A = V Λ V − 1 可行性分析 : A V = V Λ V Λ = ( v ( 1 ) , ⋯ , v ( n ) ) ( λ 1 λ 2 ⋱ λ n ) = ( λ 1 v ( 1 ) , ⋯ , λ n v ( n ) ) A V = A ( v ( 1 ) , ⋯ , v ( n ) ) = ( A v ( 1 ) , ⋯ , A v ( n ) ) A V = V A A v ( i ) = λ i v ( i ) , i = 1 , 2 , ⋯ , n λ i , v ( i ) 确实是所构造的 A 的特征值及其对应的特征向量 Λ = d i a g ( λ ) A = V\Lambda V^{−1} \\可行性分析: AV=V\Lambda \\ V\Lambda=(v^{(1)}, \cdots , v^{(n)}) \begin{pmatrix} {{\lambda _1}} & {} & {} & {} \cr {} & {{\lambda _2}} & {} & {} \cr {} & {} & \ddots & {} \cr {} & {} & {} & {{\lambda _n}} \cr \end{pmatrix} =(\lambda_1{v^{(1)}},\cdots,\lambda_n{v^{(n)}}) \\ AV=A(v^{(1)}, \cdots , v^{(n)}) =(Av^{(1)}, \cdots , Av^{(n)}) \\ AV=VA \\ Av^{(i)}=\lambda_i{v^{(i)}},i=1,2,\cdots,n \\ \lambda_i,v^{(i)}确实是所构造的A的特征值及其对应的特征向量 \\ \Lambda=diag(λ) A=VΛV−1可行性分析:AV=VΛVΛ=(v(1),⋯,v(n)) λ1λ2⋱λn =(λ1v(1),⋯,λnv(n))AV=A(v(1),⋯,v(n))=(Av(1),⋯,Av(n))AV=VAAv(i)=λiv(i),i=1,2,⋯,nλi,v(i)确实是所构造的A的特征值及其对应的特征向量Λ=diag(λ)
-
我们已经看到了构建具有特定特征值和特征向量的矩阵,能够使我们在目标方向上延伸空间。
-
然而,我们也常常希望将矩阵 分解(decompose)成特征值和特征向量。
- 分解条件和方法可以参见矩阵相似和对角化的相关知识
- n阶方阵A有n个线性无关特征向量 ( α 1 , ⋯ , α n ) (\alpha_1,\cdots,\alpha_n) (α1,⋯,αn)是A和一个对角阵相似( P − 1 A P = Λ ) P^{-1}AP=\Lambda) P−1AP=Λ)的充要条件
-
这样可以帮助我们分析矩阵的特定性质,就像质因数分解有助于我们理解整数。
-
虽然任意一个实对称矩阵 A 都有特征分解,但是特征分解可能并不唯一。
-
如果两个或多个特征向量( α 1 ( i ) , α 2 ( i ) , ⋯ \alpha^{(i)}_1,\alpha^{(i)}_2,\cdots α1(i),α2(i),⋯)拥有相同的特征值( λ i \lambda_i λi,设其重数为 n i n_i ni),那么在由这些特征向量产生的生成子空间V中的任意一组正交向量都(仍然)是该特征值对应的特征向量。
-
因此,我们可以等价地从这些特征向量中构成 Q 作为替代。
-
按照惯例,我们通常按降序排列 Λ 的元素。在该约定下,特征分解唯一当且仅当所有的特征值都是唯一的。
几何示意图
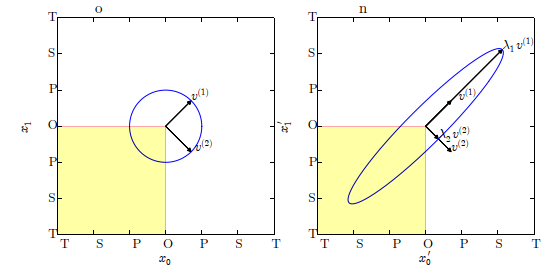
- 特征向量和特征值的作用效果。特征向量和特征值的作用效果的一个实例。
- 在这里,矩阵A 有两个标准正交的特征向量,对应特征值为 λ 1 \lambda_1 λ1 的 v ( 1 ) v^{(1)} v(1)以及对应特征值为 λ 2 \lambda_2 λ2 的 v ( 2 ) v^{(2)} v(2)
- (左) 画出了所有的单位向量 u ∈ R 2 u ∈ R^2 u∈R2 的集合,构成一个单位圆。
- (右) 画出了所有的 A u Au Au 点的集合。通过观察 A 拉伸单位圆的方式,我们可以看到它将 v ( i ) v^{(i)} v(i) 方向的空间拉伸了 λ i λ_i λi 倍。
二次型和生成子空间
-
矩阵的特征分解给了我们很多关于矩阵的有用信息。
-
矩阵是奇异的当且仅当含有零特征值。
-
实对称矩阵的特征分解也可以用于优化二次方程 f ( x ) = x ⊤ A x f(x) = x^⊤Ax f(x)=x⊤Ax
-
限制 ∥ x ∥ 2 = 1 ∥x∥_2 = 1 ∥x∥2=1,当 x 等于 A 的某个特征向量时,f 将返回对应的特征值。
-
f ( α i ) = α i T A α i = α i T λ i α i = λ i α i T α i = λ i ∣ ∣ α i ∣ ∣ 2 2 = λ i × 1 = λ i , ( ∣ ∣ α i ∣ ∣ = 1 ) f(\alpha_i)=\alpha_i^TA\alpha_i=\alpha_i^T\lambda_i\alpha_i =\lambda_i\alpha_i^T\alpha_i=\lambda_i||\alpha_i||_2^2 \\ =\lambda_i\times{1}=\lambda_i,(||\alpha_i||=1) f(αi)=αiTAαi=αiTλiαi=λiαiTαi=λi∣∣αi∣∣22=λi×1=λi,(∣∣αi∣∣=1)
-
可见,在限制条件下,函数 f f f 的最大值就是最大特征值,最小值是最小特征值。
-
-
所有特征值都是正数的矩阵被称为 正定(positive definite);所有特征值都是非负数的矩阵被称为 半正定(positive semidefinite)。同样地,所有特征值都是负数的矩阵被称为 负定(negative definite);所有特征值都是非正数的矩阵被称为 半负定(negative semidefinite)。
-
半正定矩阵受到关注是因为它们保证 ∀ x , x ⊤ A x ≥ 0 ∀x, x⊤Ax ≥ 0 ∀x,x⊤Ax≥0。此外,正定矩阵还保证 x ⊤ A x = 0 ⇒ x = 0 x^⊤Ax = 0 ⇒ x = 0 x⊤Ax=0⇒x=0。
奇异值分解
- 还有另一种分解矩阵的方法,被称为 奇异值分解(singular value decomposition, SVD)
- Singular value decomposition - Wikipedia
- 奇异值分解(singular value decomposition)是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。
- 奇异值分解在某些方面与对称矩阵或厄米矩阵基于特征向量的对角化类似。
- 然而这两种矩阵分解尽管有其相关性,但还是有明显的不同。
- 对称阵特征向量分解的基础是谱分析,而奇异值分解则是谱分析理论在任意矩阵上的推广。
理论数学风格的描述
-
假设M是一个m×n阶矩阵,其中的元素全部属于域K,也就是实数域或复数域。
-
如此则存在一个分解使得
- M = U Σ V ∗ M = U \Sigma V^* M=UΣV∗
- M = U Σ V ∗ = U Σ V ‾ T M = U \Sigma V^*=U\Sigma{\overline{V}^T} M=UΣV∗=UΣVT
-
其中U是m×m阶酉矩阵;(复数范围内的对称阵推广)
- U U ∗ = E UU^*=E UU∗=E,即 U ( U ‾ ) T = E U(\overline{U})^T=E U(U)T=E;而不是 U U T = E UU^T=E UUT=E
-
Σ是m×n阶非负实数对角矩阵;
-
而 V ∗ V^* V∗即V的共轭转置,是n×n阶酉矩阵(注意和伴随矩阵区分)。
-
这样的分解就称作M的奇异值分解。
-
实数对角阵 Σ = D ( λ 1 , ⋯ , λ n ) \Sigma=D(\lambda_1,\cdots,\lambda_n) Σ=D(λ1,⋯,λn)对角线上的元素 λ i = Σ i , i \lambda_i=\Sigma_{i,i} λi=Σi,i即为M的奇异值
- 为了和方阵对角阵 Λ = d i a g ( λ 1 , ⋯ , λ n ) \Lambda=diag(\lambda_1,\cdots,\lambda_n) Λ=diag(λ1,⋯,λn)区分开来,使用 Σ \Sigma Σ来表示更一般的对角矩阵
-
常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。
- U和V仍然不能确定。
奇异值分解和特征分解的联系😊🎈
- M ∗ M = V Σ ∗ U ∗ U Σ V ∗ = V ( Σ ∗ Σ ) V ∗ M^{*} M = V \Sigma^{*} U^{*}\, U \Sigma V^{*} = V (\Sigma^{*} \Sigma) V^{*}\, M∗M=VΣ∗U∗UΣV∗=V(Σ∗Σ)V∗
- M M ∗ = U Σ V ∗ V Σ ∗ U ∗ = U ( Σ Σ ∗ ) U ∗ M M^{*} = U \Sigma V^{*} \, V \Sigma^{*} U^{*} = U (\Sigma \Sigma^{*}) U^{*}\, MM∗=UΣV∗VΣ∗U∗=U(ΣΣ∗)U∗
- Note:对角方阵 Λ \Lambda Λ一定是对称阵( Λ T = λ \Lambda^T=\lambda ΛT=λ),但是不一定为正交阵 A T A = E A^TA=E ATA=E
- 记
A
=
M
∗
M
A=M^*M
A=M∗M,
Ω
=
Σ
∗
Σ
\Omega=\Sigma^*\Sigma
Ω=Σ∗Σ,
V
=
(
β
1
,
⋯
,
β
n
)
V=(\beta_1,\cdots,\beta_n)
V=(β1,⋯,βn)
- 则 A V = V ( Ω ) V ∗ V = V Ω E = V Ω AV=V(\Omega)V^*V=V\Omega{E}=V\Omega AV=V(Ω)V∗V=VΩE=VΩ
-
A
=
V
Ω
V
−
1
A=V\Omega{V^{-1}}
A=VΩV−1,从而可知对角方阵
Ω
=
d
i
a
g
(
λ
1
,
⋯
,
λ
n
)
\Omega=diag(\lambda_1,\cdots,\lambda_n)
Ω=diag(λ1,⋯,λn)
- A β i = λ i β i , i = 1 , 2 , ⋯ , n A\beta_i=\lambda_i\beta_i,i=1,2,\cdots,n Aβi=λiβi,i=1,2,⋯,n
- 也就是右奇异向量 β i \beta_i βi是 A = M ∗ M A=M^*M A=M∗M的关于 λ i \lambda_i λi的特征向量
- 类似的,可以推出:左奇异向量
α
i
,
i
=
1
,
2
,
⋯
,
m
\alpha_i,i=1,2,\cdots,m
αi,i=1,2,⋯,m是方阵
B
=
M
M
∗
B=MM^*
B=MM∗的关于
θ
i
\theta_i
θi的特征向量
- 其中 Λ = Σ Σ ∗ = d i a g ( θ 1 , ⋯ , θ m ) \Lambda=\Sigma\Sigma^*=diag(\theta_1,\cdots,\theta_m) Λ=ΣΣ∗=diag(θ1,⋯,θm)
机器学习风格的描述
-
将矩阵分解为 奇异向量(singular vector)和 奇异值(singular value)。
-
通过奇异值分解,我们会得到一些与特征分解相同类型的信息。
-
然而,奇异值分解有更广泛的应用。因为每个实数矩阵都有一个奇异值分解,但不一定都有特征分解。
- 例如,非方阵的矩阵没有特征分解,这时我们只能使用奇异值分解。
-
我们使用特征分解去分析矩阵 A 时,得到特征向量构成的矩阵 V和特征值构成的向量 λ,我们可以重新将 A 写作
- A = V d i a g ( λ ) V − 1 A = Vdiag(λ)V^{−1} A=Vdiag(λ)V−1
-
奇异值分解是类似的,只不过这回我们将矩阵 A 分解成三个矩阵的乘积
- A = U D V ⊤ A = UDV^⊤ A=UDV⊤
- 假设 A 是一个 m × n 的矩阵,那么 U 是一个 m × m 的矩阵,D 是一个 m × n的矩阵,V 是一个 n × n 矩阵
- 这些矩阵中的每一个经定义后都拥有特殊的结构。
- A , D ∈ R m × n A,D\in{\mathbb{R}^{m\times{n}}} A,D∈Rm×n
- U , A A T ∈ R m × m U,AA^T\in\mathbb{R}^{m\times{m}} U,AAT∈Rm×m
- V , A T A ∈ R n × n V,A^TA\in\mathbb{R}^{n\times{n}} V,ATA∈Rn×n
- 矩阵 U 和 V 都定义为正交矩阵,而矩阵 D 定义为对角矩阵(但不一定是方阵)
- U T U = E n ( U ) U^TU=E_{n(U)} UTU=En(U)
- V T V = E n ( V ) V^TV=E_{n(V)} VTV=En(V)
- 对角矩阵 D 对角线上的元素被称为矩阵 A 的 奇异值(singular value)。
- 矩阵U 的列向量 ( α 1 , ⋯ , α n ) (\alpha_1,\cdots,\alpha_n) (α1,⋯,αn)被称为 左奇异向量(left singular vector)
- 矩阵 V 的列向量 ( β 1 , ⋯ , β n ) (\beta_1,\cdots,\beta_n) (β1,⋯,βn)被称 右奇异向量(right singular vector)。
-
事实上,我们可以用与 A 相关的特征分解去解释 A 的奇异值分解。
-
A 的 左奇异向量是 A A ⊤ AA^⊤ AA⊤ 的特征向量。
-
A 的 右奇异向量是 A ⊤ A A^⊤A A⊤A 的特征向量。
-
A 的非零奇异值是 A ⊤ A A^⊤A A⊤A 特征值的平方根,同时也是 A A ⊤ AA^⊤ AA⊤ 特征值的平方根。
-
SVD 最有用的一个性质可能是拓展矩阵求逆到非方矩阵上。
-
对角矩阵的记法
- 使用 diag 函数,如 d i a g ( a 1 , a 2 , … , a n ) diag(a_1,a_2,…,a_n) diag(a1,a2,…,an) 表示一个以 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an 为主对角线元素的对角矩阵。
- 使用希腊字母 Λ \Lambda Λ 或 Δ \Delta Δ 表示一个对角矩阵,如 Λ = d i a g ( λ 1 , λ 2 , … , λ n ) \Lambda = diag(\lambda_1,\lambda_2,…,\lambda_n) Λ=diag(λ1,λ2,…,λn)。
- [ a i j ] n × n = { a i i , i = j 0 , i ≠ j [a_{ij}]_{n\times n} = \begin{cases} a_{ii}, & i=j \\ 0, & i\neq j \end{cases} [aij]n×n={aii,0,i=ji=j
酉矩阵unitary matrix
-
Unitary matrix - Wikipedia
-
酉矩阵 (wikipedia.org)
-
在线性代数中,酉矩阵(又译作幺正矩阵,英语:unitary matrix)指其共轭转置恰为其逆矩阵的复数方阵,数学描述如下:
-
U ∗ U = U U ∗ = I n U − 1 = U ∗ {\displaystyle U^{*}U=UU^{*}=I_{n}} \\ {\displaystyle U^{-1}=U^{*}} U∗U=UU∗=InU−1=U∗
-
U U ∗ = E UU^*=E UU∗=E,即 U ( U ‾ ) T = E U(\overline{U})^T=E U(U)T=E;而不是 U U T = E UU^T=E UUT=E
- 不过,当U是实矩阵时 U ‾ = U \overline{U}=U U=U,这种情况下, U U ∗ = U U T UU^*=UU^T UU∗=UUT
-
其中 U ∗ U^* U∗ 是 U 的共轭转置
- u i j = a + b k u_{ij}=a+bk uij=a+bk
- u i j ‾ = a − b k \overline{u_{ij}}=a-bk uij=a−bk
- u i j ∗ = u j i ‾ u^*_{ij}=\overline{u_{ji}} uij∗=uji
-
I n I_n In 是 n×n 单位矩阵。
-
酉矩阵是正交矩阵(元素均为实数)在复数的推广
- A T A = I n A^TA=I_n ATA=In
- U ∗ U = I n U^*U=I_n U∗U=In
-
-
例
-
U是一个正交的复矩阵:
U = [ − i 2 1 2 i 2 1 2 ] U ‾ = [ i 2 1 2 − i 2 1 2 ] U ∗ = ( U ‾ ) T = [ i 2 − i 2 1 2 1 2 ] U={\begin{bmatrix}-{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}} \\ \overline{U}={ \begin{bmatrix} {\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\ -{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\ \end{bmatrix}} \\ U^*=(\overline{U})^T={ \begin{bmatrix} {\frac {i}{\sqrt {2}}}&-{\frac {i}{\sqrt {2}}}\\ {\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\ \end{bmatrix}} U=[−2i2i2121]U=[2i−2i2121]U∗=(U)T=[2i21−2i21] -
U ∗ U = [ i 2 − i 2 1 2 1 2 ] [ − i 2 1 2 i 2 1 2 ] = [ 1 0 0 1 ] U U ∗ = [ − i 2 1 2 i 2 1 2 ] [ i 2 − i 2 1 2 1 2 ] = [ 1 0 0 1 ] {\displaystyle U^{*}U={\begin{bmatrix}{\frac {i}{\sqrt {2}}}&-{\frac {i}{\sqrt {2}}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}}{\begin{bmatrix}-{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\\\end{bmatrix}}} \\ {\displaystyle UU^{*}={\begin{bmatrix}-{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\{\frac {i}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}}{\begin{bmatrix}{\frac {i}{\sqrt {2}}}&-{\frac {i}{\sqrt {2}}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\\\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\\\end{bmatrix}}} U∗U=[2i21−2i21][−2i2i2121]=[1001]UU∗=[−2i2i2121][2i21−2i21]=[1001]
-
性质
-
U − 1 = U ∗ U^{-1}=U^* U−1=U∗
- 酉矩阵U是可逆矩阵,其逆矩阵 U − 1 U^{-1} U−1等于其共轭转置矩阵 U ∗ U^* U∗
-
∣ λ i ∣ = 1 |\lambda_i|=1 ∣λi∣=1
- 酉矩阵 U 的所有特征值 λ i \lambda_{i} λi 都是绝对值等于 1 的复数:
- 如果将U限制在实矩阵内,可以断言所有U的所有特征值 λ i \lambda_i λi也满足 ∣ λ i ∣ = 1 |\lambda_i|=1 ∣λi∣=1
-
∣ U ∣ = 1 |U|=1 ∣U∣=1
- 酉矩阵 U U U的行列式为1
Moore-Penrose 伪逆
矩阵的逆和线性方程组的解(review)
- 对于非方矩阵而言,其逆矩阵没有定义。
- 我们希望通过矩阵 A 的左逆 B 来求解线性方程: A x = y Ax = y Ax=y ,等式两边左乘左逆 B 后,我们得到 x = B y x = By x=By.
- 取决于问题的形式,我们可能无法设计一个唯一的映射将 A 映射到 B。
- 如果矩阵 A 的行数大于列数,那么上述方程可能没有解。
- 如果矩阵 A 的行数小于列数,那么上述矩阵可能有多个解。
伪逆
- Moore-Penrose 伪逆(Moore-Penrose pseudoinverse)使我们在这类问题上取得了一定的进展。
- 矩阵 A 的伪逆定义为: A + = lim α ↘ 0 ( A ⊤ A + α I ) − 1 A ⊤ A^+ = \lim\limits_{\alpha\searrow{0}}(A^⊤A +\alpha{I})^{−1}A^⊤ A+=α↘0lim(A⊤A+αI)−1A⊤
- 计算伪逆的实际算法没有基于这个定义,而是使用下面的公式:
- A + = V D + U ⊤ A^+ = VD^+U^⊤ A+=VD+U⊤
- 其中,矩阵
U
,
D
,
V
U,D,V
U,D,V 是矩阵 A奇异值分解后得到的矩阵。
- A = U D V T A=UDV^T A=UDVT
- 对角矩阵 D 的伪逆 D + D^+ D+ 是其非零元素取倒数之后再转置得到的。
应用
- 当矩阵 A 的列数多于行数时(线性方程组有解)
- 使用伪逆求解线性方程是众多可能解法中的一种。
- 特别地, x = A + y x = A^+y x=A+y 是方程所有可行解中欧几里得范数 ∥ x ∥ 2 ∥x∥_2 ∥x∥2 最小的一个。
- 当矩阵 A 的行数多于列数时,可能没有解。
- 在这种情况下,通过伪逆得到的 x x x使得 A x Ax Ax 和 y y y 的欧几里得距离 ∥ A x − y ∥ 2 ∥Ax − y∥_2 ∥Ax−y∥2 最小。
迹运算
-
T r ( A ) = ∑ i A i i Tr(A)=\sum_{i}A_{ii} Tr(A)=∑iAii
- 使用迹运算可以代替掉表达式中的某些求和号
-
迹运算可以让许多运算清楚的表示:
-
例如描述矩阵的Frobenius 范数:
-
∣ ∣ A ∣ ∣ F = ∑ i , j ( a i j ) 2 = T r ( A A T ) ||A||_F=\sqrt{\sum_{i,j}(a_{ij})^2}=\sqrt{Tr(AA^T)} ∣∣A∣∣F=i,j∑(aij)2=Tr(AAT)
-
迹运算在转置运算下是不变的: T r ( A ) = T r ( A T ) Tr(A)=Tr(A^T) Tr(A)=Tr(AT)
-
-
设 A 1 , ⋯ , A n A_1,\cdots,A_n A1,⋯,An可以连续相乘,且 A i 1 , ⋯ , A i n A_{i_1},\cdots,A_{i_n} Ai1,⋯,Ain也是可以连续乘的,那么 T r ( ∏ i A i ) = T r ( ∏ j A i j ) Tr(\prod_{i}A_i)=Tr(\prod_{j}A_{i_j}) Tr(∏iAi)=Tr(∏jAij)
- 其中 i 1 , ⋯ , i n i_1,\cdots,i_n i1,⋯,in表示 1 , ⋯ , n 1,\cdots,n 1,⋯,n的一种排列(共有 n ! n! n!中可能)
- 对于本情景,可能远没有 n ! n! n!那么多,应为不是所有的排列后能够依然能够执行连续乘法
-
类似的矩阵乘法
-
T r ( ∏ i = 1 n F ( i ) ) = T r ( F ( 1 ) ∏ i = 2 n F ( i ) ) = T r ( F ( n ) ∏ i = 1 n − 1 F ( i ) ) F ( i ) 中的 i 表示第 i 个矩阵 Tr(\prod_{i=1}^{n}F^{(i)}) =Tr(F^{(1)}\prod_{i=2}^{n}F^{(i)}) =Tr(F^{(n)}\prod_{i=1}^{n-1}F^{(i)}) \\ F^{(i)}中的i表示第i个矩阵 Tr(i=1∏nF(i))=Tr(F(1)i=2∏nF(i))=Tr(F(n)i=1∏n−1F(i))F(i)中的i表示第i个矩阵
- A ∈ R m × n A\in\mathbb{R}^{m\times{n}} A∈Rm×n,
- B ∈ R n × m B\in{\mathbb{R}^{n\times{m}}} B∈Rn×m
- T r ( A B ) = T r ( B A ) Tr(AB)=Tr(BA) Tr(AB)=Tr(BA)
-
即使循环置换后矩阵乘积的形状变了,但是妓院算的结果依然不变
-
-
另一个有用的事实是标量在迹运算后仍然是它自己: a = T r ( a ) a = Tr(a) a=Tr(a)。
方阵行列式和特征值
- 行列式,记作 det(A),是一个将方阵 A 映射到实数的函数。
- 行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。
- 如果行列式是 0,那么空间至少沿着某一维完全收缩了,使其失去了所有的体积。
- 如果行列式是 1,那么这个转换保持空间体积不变。
![推荐系统[八]算法实践总结V0:腾讯音乐全民K歌推荐系统架构及粗排设计](https://img-blog.csdnimg.cn/b935ff75e3e84d7f88de39613bb02bad.png)