👂 小宇(治愈版) - 刘大拿 - 单曲 - 网易云音乐
目录
一,安装
二,Numpy使用示例
(一)Numpy数组的创建和访问
1,创建和访问Numpy的一维数组和二维数组
2,Numpy数组的数据来源:Python列表
(二)Numpy的计算功能
1,Numpy数组的计算
2,创建矩阵和矩阵乘法
3,矩阵运算初步
全书400页,理论,代码各占一半,可以说,理论就是服务于代码的,实操性极强
当然,都是基础的代码,不过有一定难度,毕竟很厚,而一学期只有17周,每周4节课
如果想学有所成,单靠上课肯定不够的
老师说的是,平时作业必须有效果实现
大作业必须有较复杂的实现,可以通过准备人工智能比赛,作为大作业提交内容
边学边敲边参加比赛才是这门课的特色
一,安装
首先百度搜索anaconda清华镜像,第一个点进去,有个什么安装包,就是点第一个链接
然后下载anaconda,注意是Anaconda3-2019.10-Windows-x86_64.exe这个版本,也就是书里代码的版本
不要下最新的
下完后,点击“开始”,点击Anaconda Navigater,再点Jupyter Notebook,就开始在弹出来的浏览器敲代码了
当然,我一开始谈出的是HTML的visual studio,把里面url的网址粘贴复制到自己浏览器就好
二,Numpy使用示例
(一)Numpy数组的创建和访问
就是个简单的记录,一开始的内容非常简单,无非是python基础+import各种库
1,创建和访问Numpy的一维数组和二维数组
import numpy as np #导入numpy模块,指定别名为np
data = np.array([1,2,3,4,5,6,7,8,9]) #创建一个numpy一维数组
print('Numpy的一维数组:\n{0}'.format(data)) #数组内容
print('数据类型:%s'%data.dtype) #数组元素的数据类型
print('1维数组中各元素扩大10倍:\n{0}'.format(data*10))
print('访问第2个元素:{0}'.format(data[1])) #索引从0开始
data = np.array([[1,3,5,7,9],[2,4,6,8,10]]) #创建一个2行5列的numpy二维数组
print('Numpy的2维数组:\n{0}'.format(data))
print('访问二维数组中第1行第2列元素:\n{0}'.format(data[0,1])) #二维数组需要两个索引,逗号分隔
print('访问二维数组中第1行第2至第4列元素:\n{0}'.format(data[0,1:4])) #代表行和列
print('访问二维数组中第1行上的所有元素:\n'.format(data[0,:]))Numpy的一维数组:
[1 2 3 4 5 6 7 8 9]
数据类型:int32
1维数组中各元素扩大10倍:
[10 20 30 40 50 60 70 80 90]
访问第2个元素:2
Numpy的2维数组:
[[ 1 3 5 7 9]
[ 2 4 6 8 10]]
访问二维数组中第1行第2列元素:
3
访问二维数组中第1行第2至第4列元素:
[3 5 7]
访问二维数组中第1行上的所有元素:.dtype是Numpy数组的属性之一,用于存储数组元素的数据类型
2,Numpy数组的数据来源:Python列表
列表中元素数据类型可以不同,但Numpy数组的元素数据类型必须相同
以下代码创建列表,并将列表转化为Numpy数组
data = [[1,2,3,4,5,6,7,8,9],['A','B','C','D','E','F','G','H','I']] #创建Python二维列表
print('data是Python的列表(list):\n{0}'.format(data))
MyArray1 = np.array(data) #列表转化为Numpy数组
print('MyArray1是Numpy的N维数组:\n%s\nMyArray1的形状:%s'%(MyArray1, MyArray1.shape)) #数组内容和形状data是Python的列表(list):
[[1, 2, 3, 4, 5, 6, 7, 8, 9], ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']]
MyArray1是Numpy的N维数组:
[['1' '2' '3' '4' '5' '6' '7' '8' '9']
['A' 'B' 'C' 'D' 'E' 'F' 'G' 'H' 'I']]
MyArray1的形状:(2, 9)1,(2, 9)表示2行9列
2,第3行列表转数组时,由于数组要求数据类型一致,自动将数值型 --> 字符型
3,.shape是Numpy数组对象的属性之一,用于存储数组的行数和列数
(二)Numpy的计算功能
1,统计量 2,新变量 3,矩阵计算
1,Numpy数组的计算
MyArray2 = np.arange(10) #生成0至9的一维数组
print('MyArray2:\n{0}'.format(MyArray2))
print('MyArray2的基本描述统计量:\n均值:%f,标准差%f,总和:%f,最大值:%f'%(MyArray2.mean(),MyArray2.std(),MyArray2.sum(),MyArray2.max()))
print('MyArray2的累计和:{0}'.format(MyArray2.cumsum())) #累计和
print('MyArray2开平方:{0}'.format(np.sqrt(MyArray2))) #开平方
np.random.seed(123) #指定随机数种子
MyArray3 = np.random.randn(10) #符合正态分布
print('MyArray3:\n{0}'.format(MyArray3))
print('MyArray3排序结果:\n{0}'.format(np.sort(MyArray3))) #排序
print('四舍五入到最近整数:\n{0}'.format(np.rint(MyArray3))) #四舍五入
print('各元素的正负号:\n{0}'.format(np.sign(MyArray3))) #判断正负符号
print('各元素非负显示"正",负数显示"负":\n{0}'.format(np.where(MyArray3>0,'正','负')))
print('MyArray2+MyArray3的结果:\n{0}'.format(MyArray2+MyArray3)) #相加MyArray2:
[0 1 2 3 4 5 6 7 8 9]
MyArray2的基本描述统计量:
均值:4.500000,标准差2.872281,总和:45.000000,最大值:9.000000
MyArray2的累计和:[ 0 1 3 6 10 15 21 28 36 45]
MyArray2开平方:[0. 1. 1.41421356 1.73205081 2. 2.23606798
2.44948974 2.64575131 2.82842712 3. ]
MyArray3:
[-1.0856306 0.99734545 0.2829785 -1.50629471 -0.57860025 1.65143654
-2.42667924 -0.42891263 1.26593626 -0.8667404 ]
MyArray3排序结果:
[-2.42667924 -1.50629471 -1.0856306 -0.8667404 -0.57860025 -0.42891263
0.2829785 0.99734545 1.26593626 1.65143654]
四舍五入到最近整数:
[-1. 1. 0. -2. -1. 2. -2. -0. 1. -1.]
各元素的正负号:
[-1. 1. 1. -1. -1. 1. -1. -1. 1. -1.]
各元素非负显示"正",负数显示"负":
['负' '正' '正' '负' '负' '正' '负' '负' '正' '负']
MyArray2+MyArray3的结果:
[-1.0856306 1.99734545 2.2829785 1.49370529 3.42139975 6.65143654
3.57332076 6.57108737 9.26593626 8.1332596 ]1,np.range()生成指定范围取值的一维数组
2,.mean()计算数组元素的均值
.std()标准差,.sum()总和,.max()最大值
3,数组方法.cumsum()累加和
4,Numpy函数sqrt()开平方
5,Numpy函数seed()指定随机数种子(保证随机数不同)
6,Numpy函数random.randn()生成包含n个符合正态分布元素的一维数组
7,numpy.sort()排序,numpy.rint()四舍五入,numpy.where()依次对数组元素逻辑判断
2,创建矩阵和矩阵乘法
机器学习数据建模过程中,常见的运算
np.random.seed(123)
X = np.floor(np.random.normal(5, 1, (2, 5))) #得到2行5列二维数组X(矩阵)
Y = np.eye(5) #5行5列单位矩阵Y
print('X:\n{0}'.format(X))
print('Y:\n{0}'.format(Y))
print('X和Y的点积:\n{0}'.format(np.dot(X, Y))) #矩阵乘积X:
[[3. 5. 5. 3. 4.]
[6. 2. 4. 6. 4.]]
Y:
[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]]
X和Y的点积:
[[3. 5. 5. 3. 4.]
[6. 2. 4. 6. 4.]]1,numpy.random.normal(5, 1, (2, 5))生成2行5列,均值5,标准差1的服从正态分布的数组元素
2,numpy.floor()得到距各元素最近的最大整数
3,numpy.eye(n)生成n行n列单位矩阵
4,numpy.dot(X, Y)计算矩阵X和Y的矩阵乘积
3,矩阵运算初步
只能说跟着敲完一遍,让自己写还是写不出来,还得背
除了矩阵的乘法,矩阵中还有其他重要的矩阵运算,
比如矩阵的逆,特征值,特征向量,奇异值分解...
from numpy.linalg import inv,svd,eig,det #导入numpy的linalg模块的函数
X = np.random.randn(5,5) #生成5行5列符合正态分布的矩阵
print(X)
mat = X.T.dot(X) #X.T是X的转置, .dot(X)转置后结果与X相乘
print(mat)
print('矩阵mat的逆:\n{0}'.format(inv(mat))) #inv矩阵的逆
print('矩阵mat的行列式值:\n{0}'.format(det(mat))) #det行列式值
print('矩阵mat的特征值和特征向量:\n{0}'.format(eig(mat))) #eig特征值和对应的特征向量
print('对矩阵mat作奇异值分解:\n{0}'.format(svd(mat))) #svd对矩阵进行奇异值分解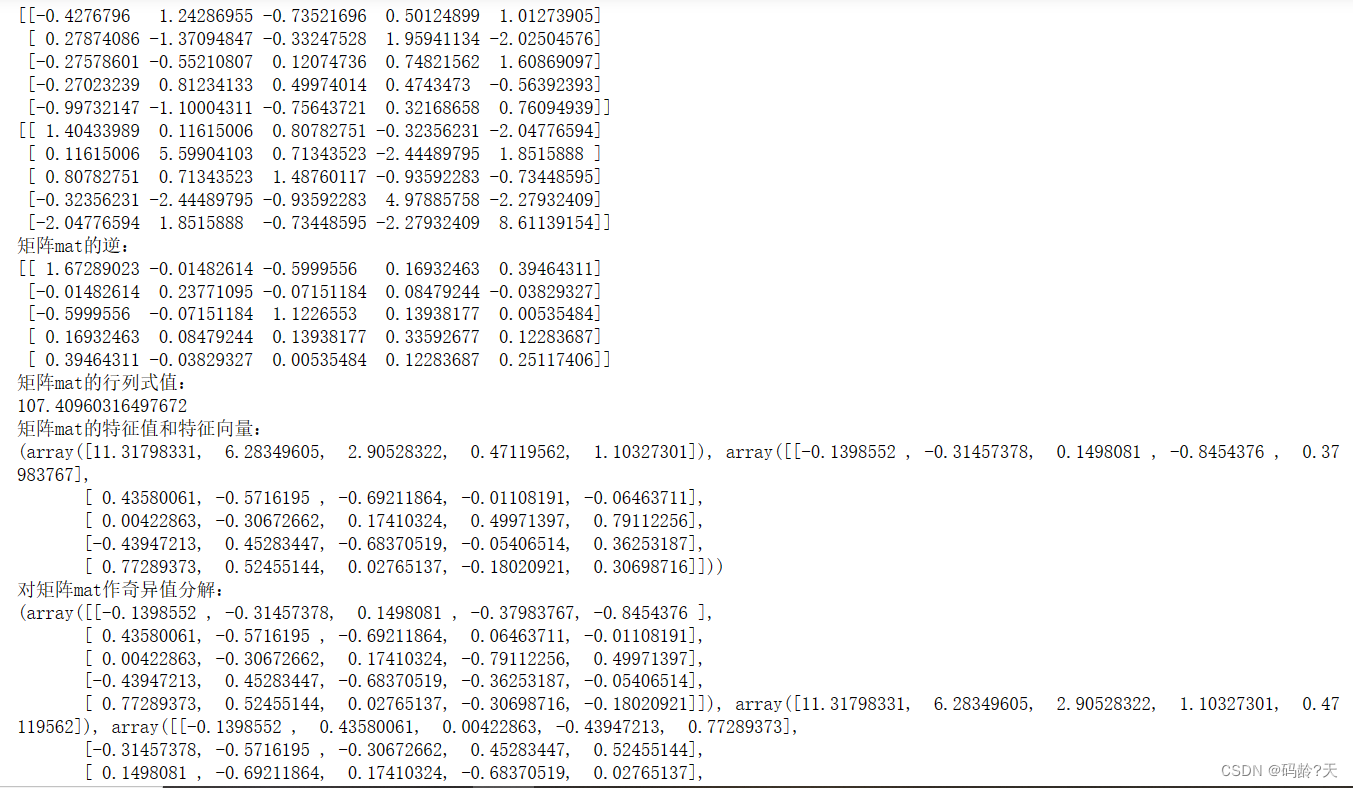
知识点在注释里