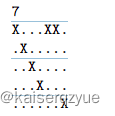题目链接：Pipeline Scheduling
题目描述：

给定一张$5\times n(1\le n\le 20)$的资源需求表，第$i$行第$j$列的值为’X’表示进程在$j$时刻需要使用使用资源$i$，如果为’.'则表示不需要使用。你的任务是安排十个相同进程的启动时间，使得所有进程完成的时间尽可能的早。在安排每个进程的开始时间你需要注意：

• 一个进程一旦开始就必须要一直执行，而不能停止；
• 任意一个资源必须进行互斥使用，也就是任意时刻$j$需要保证对于$1\le i\le 5$，$i$资源最多只被一个进程所使用。

你需要输出最早的完成时间。
例如输入为：

对应的输出应该是$34$，对应的每个进程的执行情况如下表（图中的编号代表进程的编号）：

题解：

本题不难想到的暴力方法是，枚举十个进程的开始时间，由于一共有十个进程每个进程开始的时间范围为：$[0,n]$，所以时间复杂度为$O(n^{10})$。
这样需要枚举的状态太多了，如何减少状态呢？在我们已知每个资源关于时间的需求情况实际上我们可以知道并不是$[0,n]$所有的开始时间都是可行的，我们能够确定出有限个可行的开始时间。我们设当前进程相对于上一个进程晚开始$delayTime$，那么此时当前的进程会在那些时刻占用那些资源是可以确定的，而只有当前进程占用的资源与上一个进程占用的资源不存在冲突的时候$delayTime$才是可行的，如果能够提前计算出所有的$delayTime$，那么最后进行枚举的时候复杂度就会大大减少。
如何快速判断一个$delayTime$是否可行？我们可以用二进制来保存每个资源与时间的关系，例如样例的输入我们可以用二进制表示为：
$$\begin{gathered} status[0]=0110001 \\ status[1]=0000010 \\ status[2]=0000100 \\ status[3]=0001000 \\ status[4]=1000000 \end{gathered}$$
而当前进程相对于上一个进程延迟$delayTime$后开始，那么上一个进程在当前进程的各个资源占用会产生影响的部分实际上是$status[i]>>delayTime$（注意这里使用的二进制表示和图上是颠倒的，所以此处需要用右移表示时间的流逝，而如果不颠倒处理需要进行特定的位数判断比较麻烦），而当前进程的资源使用情况就是$status[i]$，所以只要KaTeX parse error: Expected 'EOF', got '&' at position 11: status[i] &̲ (status[i] >>d…就代表资源$i$不会发生冲突，只有五个资源都不发生冲突的$delayTime$才是可行的。
还有剪枝方法吗？实际上这样应该能够通过大部分数据，但是我们还有一个比较简单的剪枝，但是这个剪枝能够去除掉很多的状态。我们需要记录一个$minDelayTime$表示所有$delayTime$中的最小值，如果$nowStartTime+restProcessNum\times minDelayTime+n\ge nowAns$，那么我们直接进行剪枝即可（即假设后续所有的进程都能最早开始但是依然不能早于当前记录的答案时进行减值）。

代码：

#include <bits/stdc++.h>

const int INF = 0x3f3f3f3f;
const int UNIT_NUM = 5;
const int PROCESS_NUM = 10;

using namespace std;

int ans, n, minDelayTime;
int status[UNIT_NUM];
string reservationTable;
vector<int> nextStep;

void init()
{
    nextStep.resize(0);
    ans = INF;
    minDelayTime = -1;
    for (int delayTime = 1; delayTime <= n; delayTime++) {
        bool canStart = true;
        for (int unitID = 0; unitID < UNIT_NUM; unitID++) {
            if ((status[unitID] >> delayTime) & status[unitID]) {
                canStart = false;
                break;
            }
        }
        if (canStart) {
            if (minDelayTime == -1) { minDelayTime = delayTime; }
            nextStep.push_back(delayTime);
        }
    }
}

void dfs(int nowDepth, int nowStartTime, int s0, int s1, int s2, int s3, int s4) {
    if (nowDepth == PROCESS_NUM - 1) { // 这里等于PROCESS_NUM - 1是因为0号进程已经安排到0时刻开始，后续安排的是1-9号进程
        ans = min(ans, nowStartTime + n);
        return ;
    }
    if (nowStartTime + (9 - nowDepth) * minDelayTime + n >= ans) { return; }
    for (int delayTime : nextStep) {
        int ns0 = s0 >> delayTime, ns1 = s1 >> delayTime, ns2 = s2 >> delayTime, ns3 = s3 >> delayTime, ns4 = s4 >> delayTime;
        if ((ns0 & status[0]) || (ns1 & status[1]) || (ns2 & status[2]) || (ns3 & status[3]) || (ns4 & status[4])) {continue; }
        dfs(nowDepth + 1, nowStartTime + delayTime, ns0 | status[0], ns1 | status[1], ns2 | status[2], ns3 | status[3], ns4 | status[4]);
    }
}

int main()
{
    ios::sync_with_stdio(false);
    while (cin >> n && n != 0) {
        for (int i = 0; i < UNIT_NUM; i++) {
            cin >> reservationTable;
            status[i] = 0;
            for (int j = 0; j < n; j++) {
                if (reservationTable[j] == 'X') {
                    status[i] |= 1 << j;
                }
            }
        }
        init();
        dfs(0, 0, status[0], status[1], status[2], status[3], status[4]);
        cout << ans << endl;
    }
    return 0;
}