C语言详解求两个正数最小公倍数的3种境界~😎
- 前言🙌
- 必备小知识~😘
- 求最小公倍数境界1~ 😊
- 求最小公倍数境界2~ 😊
- 求最小公倍数境界3~ 😊
- 总结撒花💞

博客昵称:博客小梦😊
最喜欢的座右铭:全神贯注的上吧!!!
作者简介:一名热爱C/C++,算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主!
博主小留言:哈喽!😄各位CSDN的uu们,我是你的博客好友小梦,希望我的文章可以给您带来一定的帮助,话不多说,文章推上!欢迎大家在评论区唠嗑指正,觉得好的话别忘了一键三连哦!😘
前言🙌
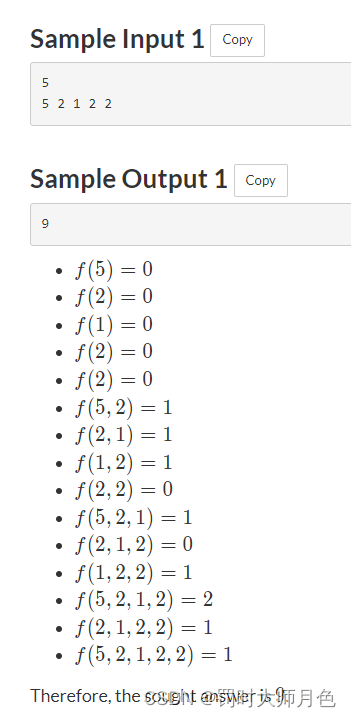
哈喽各位友友们😊,我今天又学到了很多有趣的知识,现在迫不及待的想和大家分享一下!😘我仅已此文,手把手用C语言详解求两个正数最小公倍数的3种境界!这里举个求正数23 和正数 1782的最小公倍数为例。都是精华内容,可不要错过哟!!!😍😍😍
必备小知识~😘
什么是最小公倍数和最大公约数(最大公因数)?
- 最小公倍数就是可以整除这两个数的最小的数,例如:6和9的最小公倍数就是18,3和5的最小公倍数是15。==也可以说是两个数相乘除以他们的最大公约数==。
- 最大公约数的概念和最小公倍数正好相反,就是两个数都可以整除的最大的数,如3和5的最大公约数就是1,而6和9的最大公约数就是3。
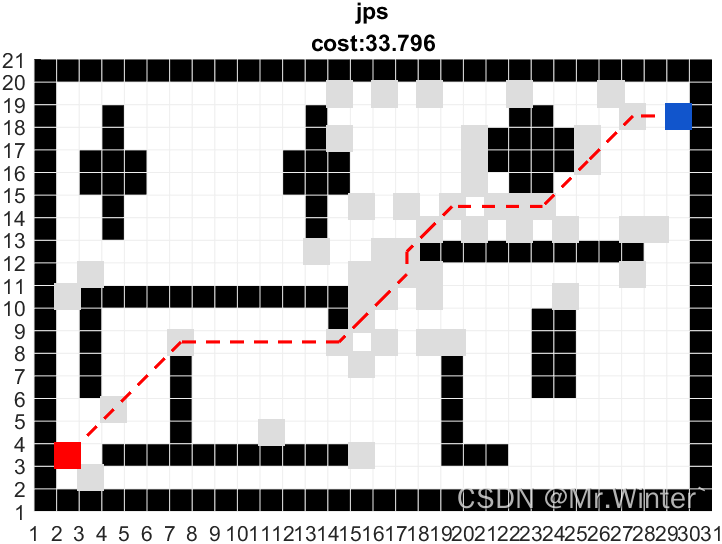
求最小公倍数境界1~ 😊
境界1的算法求解过程分析:
- 这里的变量count 主要是求其循环比较的次数,通过这个可以比较看出三种境界算法的优劣性。
- 先定义一个count变量存储这两个数的最大值。
- 如果满足 max % a != 0 || max % b != 0,就让最大值加1,直到有一个能够被a和b同时整除的数就退出循环,这个数就是a和b的最小公倍数。
境界1源码: 😍
#include <stdio.h>
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
int count = 0;
int max = a > b ? a : b;//先找到最大值
while (max % a != 0 || max % b != 0)
{
max++;
count++;
}
printf("最小公倍数 = %d,比较运行的次数 = %d ", max,count);
return 0;
}
代码结果运行图: 😍
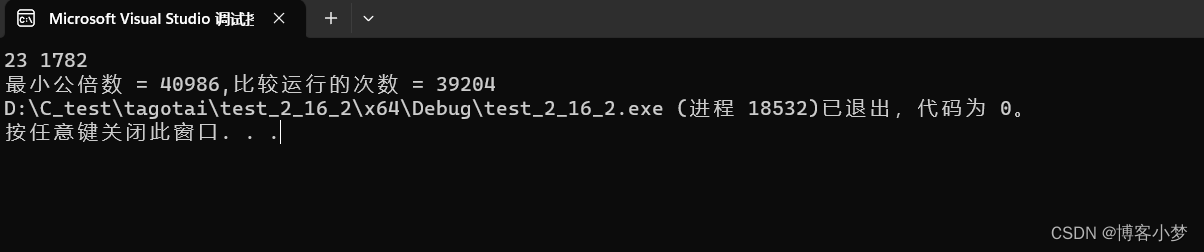 可见count = 39204 ,这个循环比较次数为39204,可见其算法效率非常低效。有没有更好的算法呢?请耐心看下文分析~
可见count = 39204 ,这个循环比较次数为39204,可见其算法效率非常低效。有没有更好的算法呢?请耐心看下文分析~
求最小公倍数境界2~ 😊
境界2的算法求解过程分析:
- 这里的变量count 主要是求其循环比较的次数,通过这个可以比较看出三种境界算法的优劣性。
- 定义一个变量i,让它从1开始,符合条件就自增。一个数的i倍,即乘以i其表达式结果就是这个数倍数,如果可以被另一个数整除,说明这个倍数就是这两个数的公倍数。因为i是从1开始自增的,所以第一个满足这个条件的一定是这两个数的最小公倍数啦。
境界2源码: 😍
#include <stdio.h>
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
int i = 1;
int count = 0;
while (i*a % b != 0)
{
i++;
count++;
}
printf("最小公倍数 = %d,比较运行的次数 = %d ",i*a,count);
return 0;
}
代码结果运行图: 😍
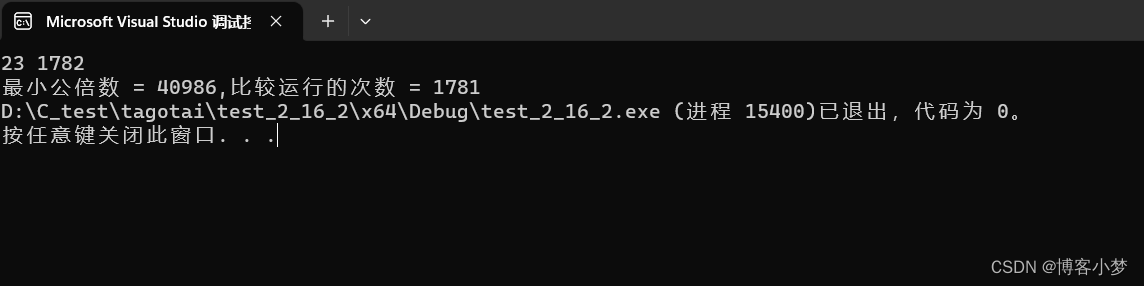
可见count = 1781 ,这个循环比较次数为1781,可见其算法效率比境界一有了明显的改善!那还有没有比这个更好的算法呢?请耐心看下文分析~
求最小公倍数境界3~ 😊
辗转相除法流程图解:
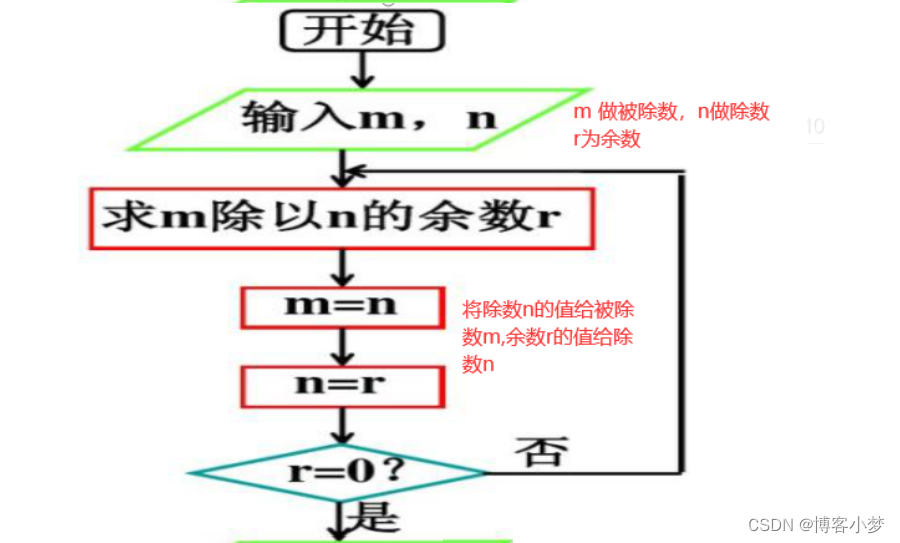
境界3源码: 😍
#include <stdio.h>
int main()
{
int m = 0;
int n = 0;
scanf("%d %d", &m, &n);
int a = m * n;
int r = 0;
int count = 0;
while (r = m % n)
{
m = n;
n = r;
count++;
}
printf("最小公倍数 = %d,比较运行的次数 = %d ", a / n, count);
return 0;
}
代码结果运行图: 😍
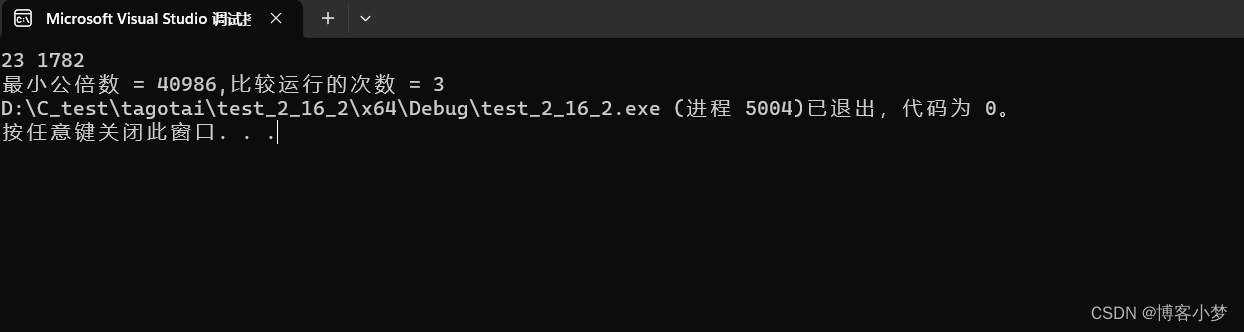
可见count = 3 ,这个循环比较次数为3,可见其算法效率真的是太惊人了!,但是这个算法还是有一个缺点,就是变量 a = m * n。如果这两个数很大,可能它们相乘的结果太大超出类型的最大数值。
总结撒花💞
本篇文章旨在带领大家利用C语言详解 - 求两个正数最小公倍数的3种境界。希望大家通过阅读此文有所收获!😘如果我写的有什么不好之处,请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘

![[Incognito 4.0] ictf 2023](https://img-blog.csdnimg.cn/img_convert/9ccae03e857599815611724474a40281.png)