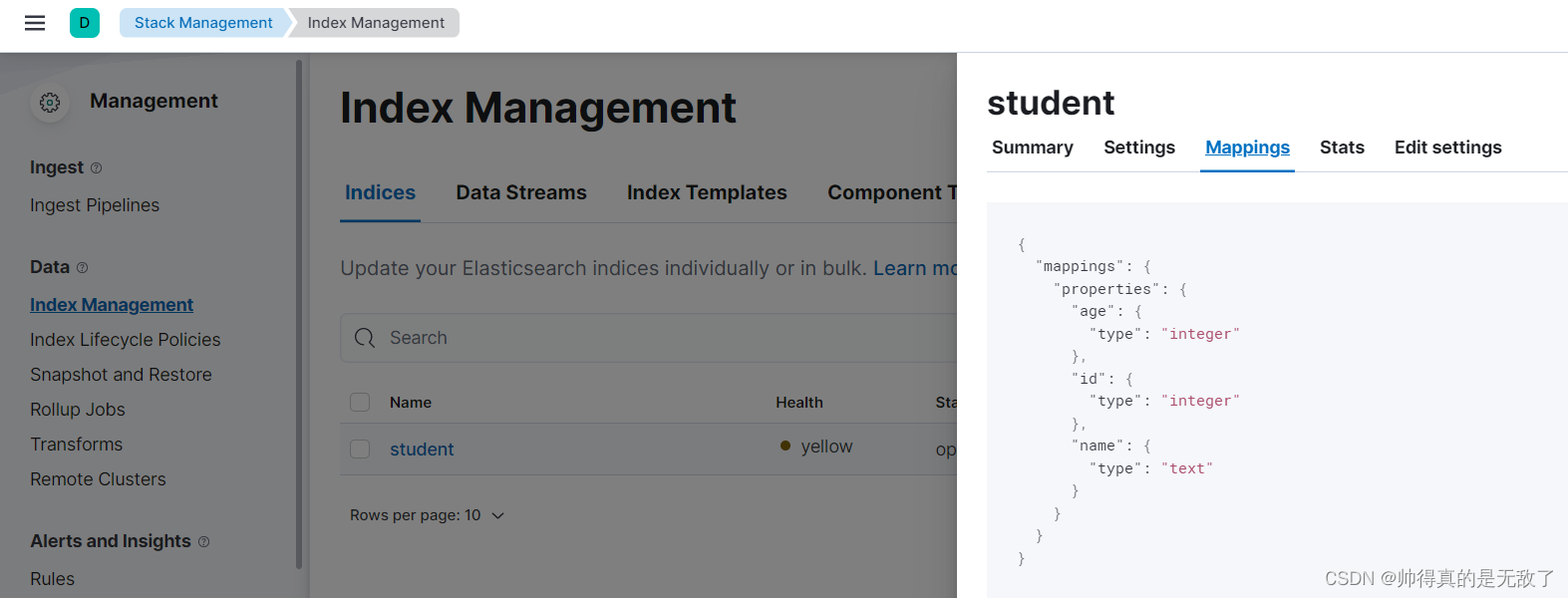
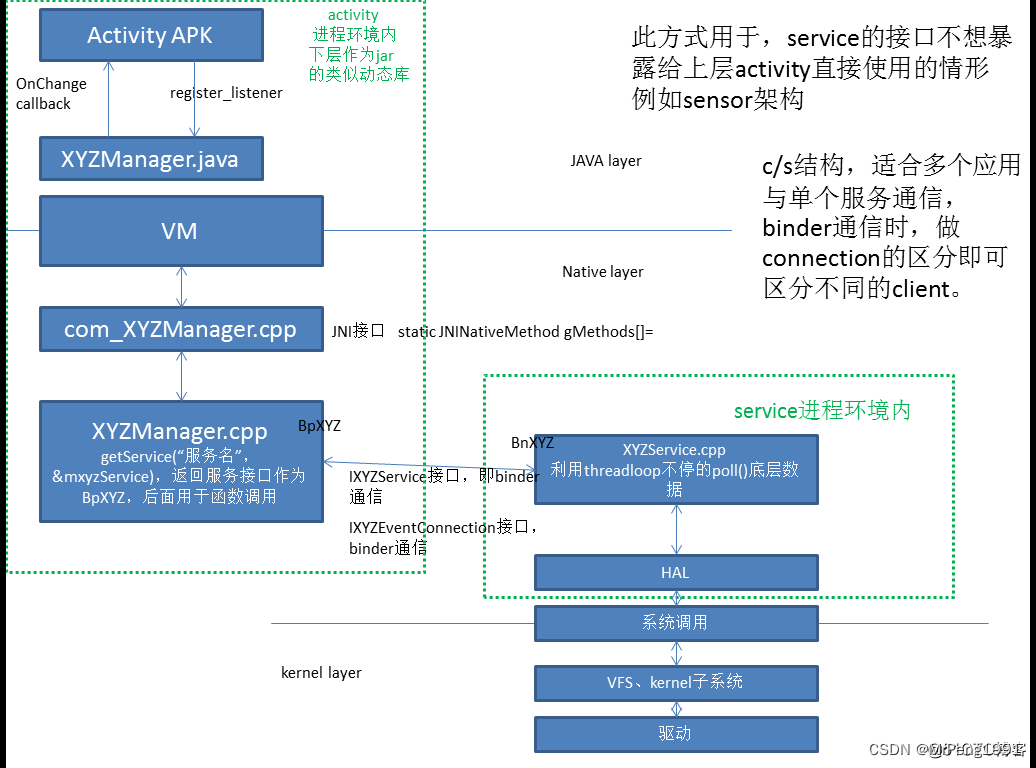
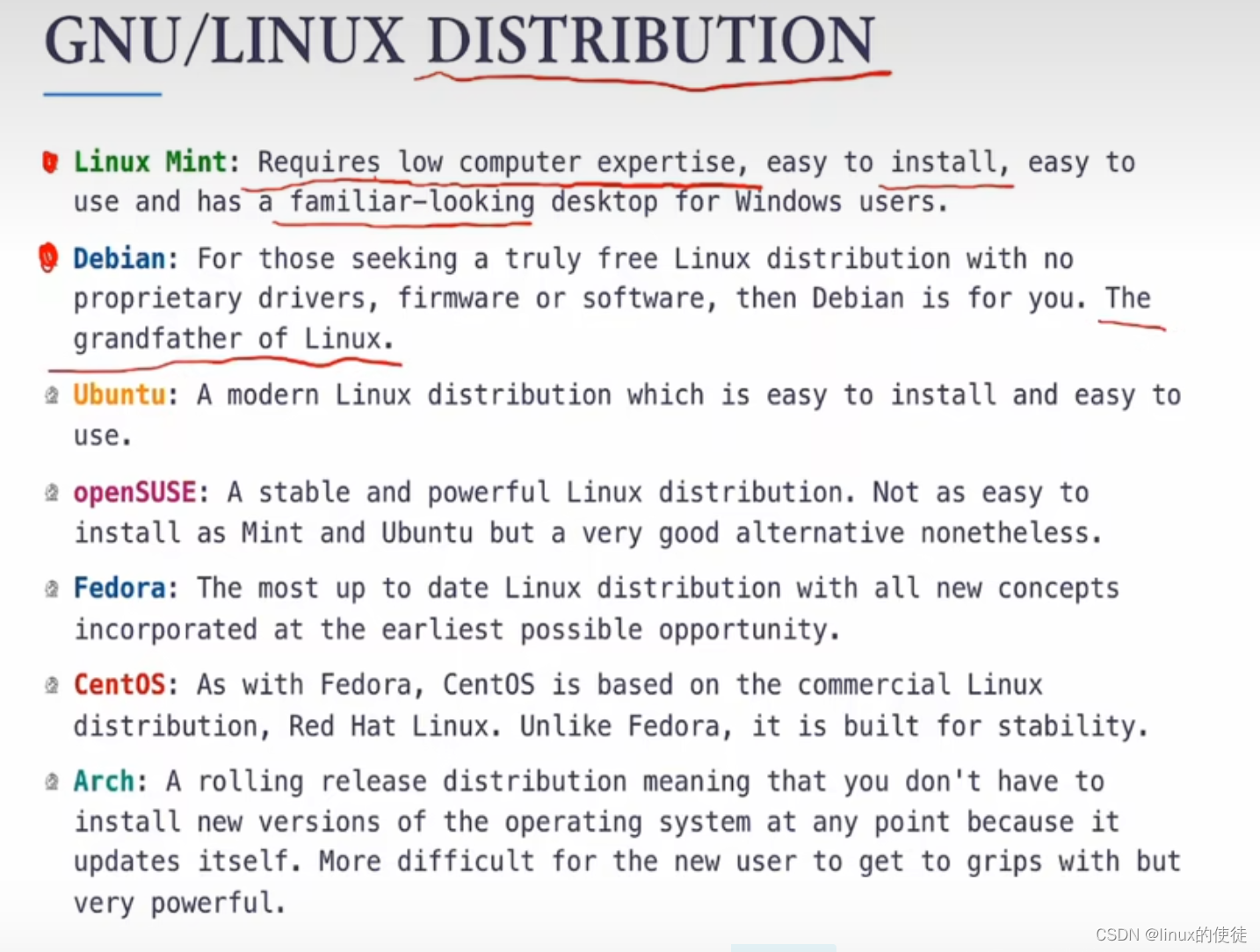
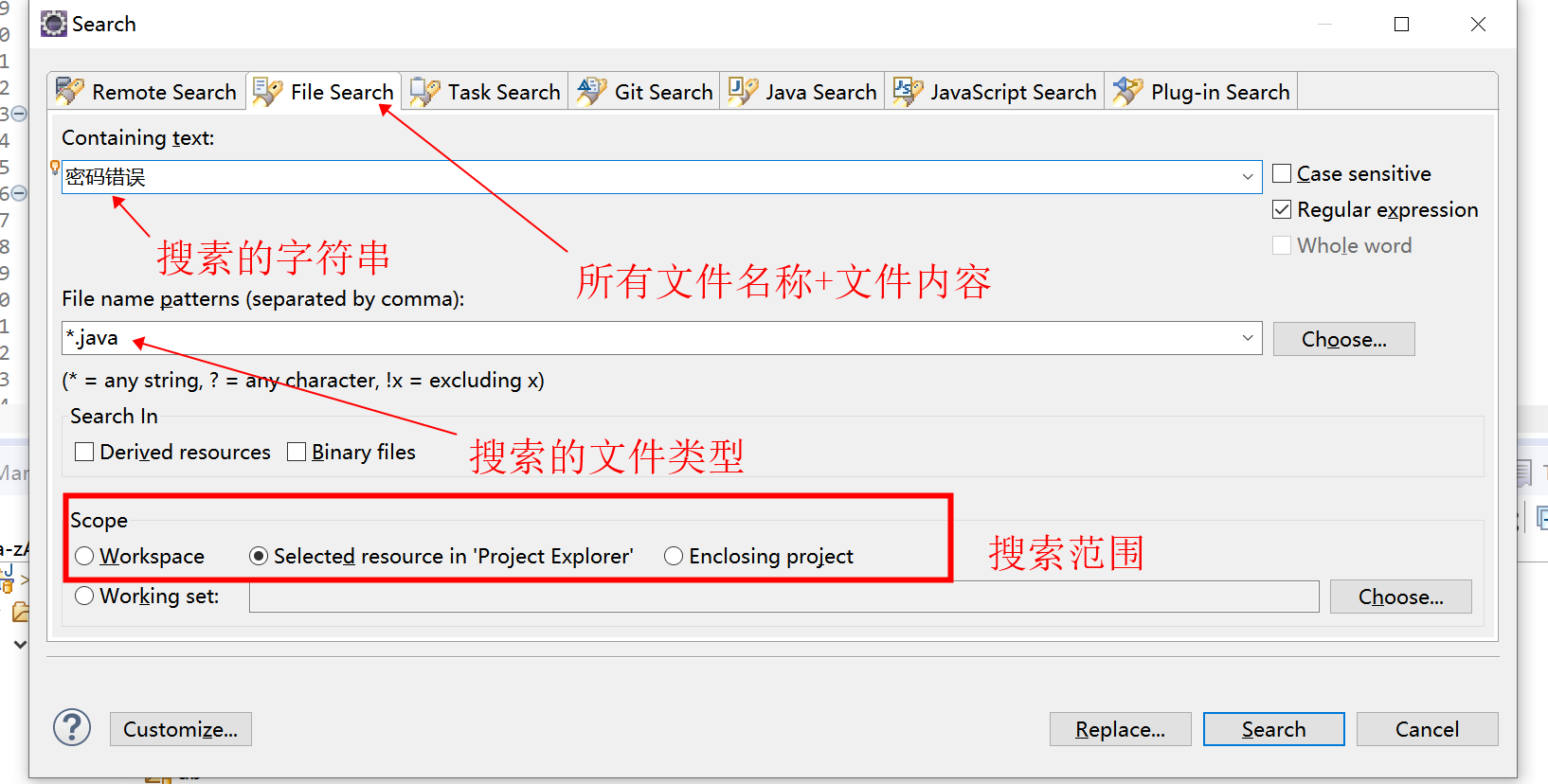
ABC比较简单就不再复述
D - Marking
简要题意 :给你一个长度为
n
n
n的数组,下标为
0
到
n
−
1
0 到 n-1
0到n−1,最初指针位于0,重复执行n-1次操作,每次操作的定义为将当前指针加上
d
d
d,如果该位置为空(未填数),否则我们向右找到第一个为空的位置
(
x
=
(
x
+
1
)
(x = (x + 1) % n)
(x=(x+1),然后把当前位置赋值,问第
k
k
k次操作的找到的位置是哪个。

思路:
我们可以比较容易的发现,这道题考察了裴蜀定理,结论是会分成
g
c
d
(
n
,
d
)
gcd(n , d)
gcd(n,d)个环,每个环会走
n
/
g
c
d
(
n
,
d
)
n / gcd(n,d)
n/gcd(n,d)步,然后我们分类讨论在哪个环,然后位于哪个环的位置即可。
代码
E - Make it Palindrome
简要题意 : 给你一个数组,问你所有的连续子数组形成回文串最少需要多少次修改,并输出总和。
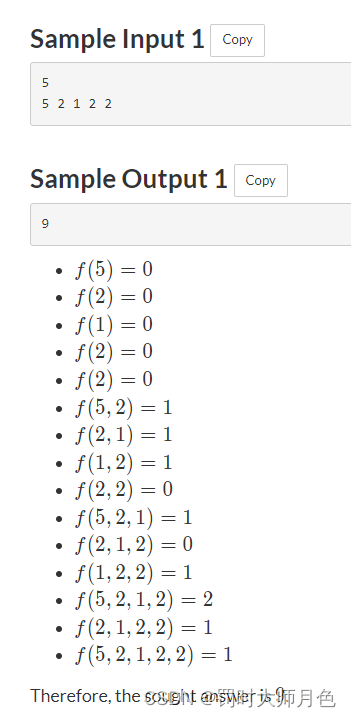
思路 :我们考虑单独考虑每一对对答案的影响,我们考虑如果这一对不同,他对答案的影响是
m
i
n
(
i
,
n
−
j
+
1
)
min(i , n - j + 1)
min(i,n−j+1),然后我们对半考虑统计答案贡献即可,对半考虑离左右边界较近的点对答案的影响,比如
(
5
,
j
)
(5 , j)
(5,j)我们发现
j
j
j为
[
5
,
j
−
5
+
1
]
[5 , j - 5 + 1]
[5,j−5+1]时答案是以左边界为准,所以可以比较好的维护答案。
代码