0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 A*算法的弊端

A*算法是非常有效且常用的路径规划算法之一，其是结合Dijsktra算法与GBFS各自优势的启发式搜索算法，其具体原理请参考路径规划 | 图解A*、Dijkstra、GBFS算法的异同(附C++/Python/Matlab仿真)。然而，A*算法有个明显的缺陷——拓展了太多的无用节点

例：如图所示，从起点 $s$ 到终点 $g$ 有三条可行路线：

$L_1=\left\{ \left( 1,2 \right) \rightarrow \left( 2,3 \right) \rightarrow \left( 3,2 \right) \right\}$
$L_2=\left\{ \left( 1,2 \right) \rightarrow \left( 2,2 \right) \rightarrow \left( 3,2 \right) \right\}$
$L_3=\left\{ \left( 1,2 \right) \rightarrow \left( 2,1 \right) \rightarrow \left( 3,2 \right) \right\}$

直观地，路径 $L_1$ 、 $L_3$ 的探索对最优路径的生成时没有意义的，但传统A*算法仍会在扩展邻域时评估这些不必要的节点，例如图中的灰色栅格，造成其应用时存在内存消耗大、运行时间长等缺陷

2 跳点搜索算法

2.1 自然与强制邻点

针对A*算法的缺陷，Harabor等提出跳点搜索算法(Jump Point Search, JPS)，筛选出有价值的节点——称为跳点而剪去那些无意义的冗余节点。

设 $n$ 是节点 $x$ 的邻接点， $p$ 是节点 $x$ 的父节点，节点 $x$ 的邻域采用八邻域法，则跳点剪枝策略中的基本概念如下：

自然邻点：当节点 $x$ 邻域不存在障碍时(暂时移除障碍)，若从 $p$ 出发任意不经过节点 $x$ 到达 $n$ 的路径 $<p,\cdots ,n|x>$ 比经过 $x$ 到达 $n$ 的路径 $<p,\cdots ,x,\cdots ,n>$ 长，即
$\begin{cases} L\left( <p,\cdots ,n|x> \right) \geqslant L\left( <p,\cdots ,x,\cdots ,n> \right) , p\text{是}x\text{的对角节点}\\ L\left( <p,\cdots ,n|x> \right) >L\left( <p,\cdots ,x,\cdots ,n> \right) , \mathrm{otherwise}\\\end{cases}$
恒成立，则称邻接点 $n$ 是节点 $x$ 在父节点是 $p$ 时的自然邻点
强制邻点：当节点 $x$ 的邻域存在障碍时，若从 $p$ 出发任意不经过节点 $x$ 到达 $n$ 的路径 $<p,\cdots ,n|x>$ 比经过节点 $x$ 到达 $n$ 的路径 $<p,\cdots ,x,\cdots ,n>$ 长，且节点 $n$ 不是节点 $x$ 的自然邻点，则称邻接点 $n$ 是节点 $x$ 在父节点是 $p$ 时的强制邻点，如图所示为水平搜索与斜搜索情况下的八种强制邻点情况。

在这里插入图片描述

2.2 跳点剪枝策略

跳点本质上是搜索方向可能发生改变的点，其筛选规则为

若节点 $x$ 是终点，则节点 $x$ 是跳点；
若节点 $x$ 存在至少一个强制邻点，则节点 $x$ 是跳点；
在斜向搜索时，若节点 $x$ 在水平或垂直分量上有跳点，则节点 $x$ 是跳点

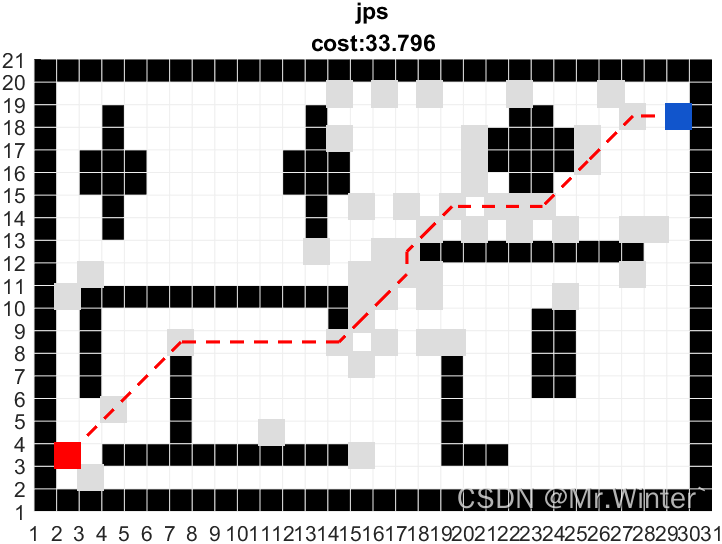
用一个实例说明。如图所示的栅格地图中，绿色是起点，红色是终点，黑色是障碍物

在这里插入图片描述
我们首先用A*算法看看规划的路径，其中绿色是开节点表中的节点，蓝色是闭节点表中的节点，黄色是规划路径

在这里插入图片描述
再用JPS算法执行路径规划，灰色的是在搜索过程中被跳过的点，而绿色节点就是跳点，实际应用于算法搜索中的节点(绿色和蓝色)，与A*算法相比大幅度减少。

在这里插入图片描述

3 算法仿真与实现

3.1 算法流程

JPS算法的核心就是jump()函数，我采用递归方法来实现，使得整体代码量下降，且逻辑更清晰明确。总的思路就是实现跳点剪枝的三条策略

若节点 $x$ 是终点，则节点 $x$ 是跳点；
若节点 $x$ 存在至少一个强制邻点，则节点 $x$ 是跳点；
在斜向搜索时，若节点 $x$ 在水平或垂直分量上有跳点，则节点 $x$ 是跳点

在这里插入图片描述
跳点剪枝策略就是通过筛选跳点作为探索域，而忽略对搜索路径没有实质影响的冗余节点，实现大幅度降低计算复杂度的效果。JPS算法最大的优势是在障碍密集的情况下，相较传统A*算法的计算速度一般有量级的提升；缺陷是其不能应用于广义图搜索，只适用于栅格地图。

3.2 ROS C++实现

Node JumpPointSearch::jump(const Node& point, const Node& motion)
{
  Node new_point = point + motion;
  new_point.id_ = this->grid2Index(new_point.x_, new_point.y_);
  new_point.pid_ = point.id_;
  new_point.h_ = std::sqrt(std::pow(new_point.x_ - this->goal_.x_, 2) + std::pow(new_point.y_ - this->goal_.y_, 2));

  // next node hit the boundary or obstacle
  if (new_point.id_ < 0 || new_point.id_ >= this->ns_ || this->costs_[new_point.id_] >= this->lethal_cost_ * this->factor_)
    return Node(-1, -1, -1, -1, -1, -1);

  // goal found
  if (new_point == this->goal_)
    return new_point;

  // diagonal
  if (motion.x_ && motion.y_)
  {
    // if exists jump point at horizontal or vertical
    Node x_dir = Node(motion.x_, 0, 1, 0, 0, 0);
    Node y_dir = Node(0, motion.y_, 1, 0, 0, 0);
    if (this->jump(new_point, x_dir).id_ != -1 || this->jump(new_point, y_dir).id_ != -1)
      return new_point;
  }

  // exists forced neighbor
  if (this->detectForceNeighbor(new_point, motion))
    return new_point;
  else
    return this->jump(new_point, motion);
}

在这里插入图片描述

3.3 Python实现

def jump(self, node: Node, motion: Node):
    # explore a new node
    new_node = node + motion
    new_node.parent = node.current
    new_node.h = self.h(new_node, self.goal)

    # hit the obstacle
    if new_node.current in self.obstacles:
        return None

    # goal found
    if new_node == self.goal:
        return new_node

    # diagonal
    if motion.current[0] and motion.current[1]:
        # if exists jump point at horizontal or vertical
        x_dir = Node((motion.current[0], 0), None, 1, None)
        y_dir = Node((0, motion.current[1]), None, 1, None)
        if self.jump(new_node, x_dir) or self.jump(new_node, y_dir):
            return new_node
        
    # if exists forced neighbor
    if self.detectForceNeighbor(new_node, motion):
        return new_node
    else:
        return self.jump(new_node, motion)

在这里插入图片描述

3.4 Matlab实现

function [new_node, flag] = jump(cur_node, motion, goal, map)
    flag = false;

    % explore a new node
    new_node = [cur_node(1) + motion(1), ...
                      cur_node(2) + motion(2), ...
                      cur_node(3) + motion(3), ...
                      0, cur_node(1), cur_node(2)
                      ];
    new_node(4) = h(new_node(1:2), goal);

    % obstacle
    if new_node(1) <= 0 || new_node(2) <= 0 || map(new_node(1), new_node(2)) == 2
        return
    end

    % goal found
    if new_node(1) == goal(1) && new_node(2) == goal(2)
        flag = true;
        return
    end

    % diagonal
    if motion(1) && motion(2)
        % if exists jump point at horizontal or vertical
        x_dir = [motion(1), 0, 1];
        y_dir = [0, motion(2), 1];
        [~, flag_x] = jump(new_node, x_dir, goal, map);
        [~, flag_y] = jump(new_node, y_dir, goal, map);
        if  flag_x || flag_y 
            flag = true;
            return
        end
    end
            
    % if exists forced neighbor
    if detect_force(new_node, motion, map)
        flag = true;
        return
    else
        [new_node, flag] = jump(new_node, motion, goal, map);
        return
    end
end