有序表的应用：[Leetcode 327] 区间和的个数

news2025/1/11 5:14:11

一、题目

1、题目描述

给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中，值位于范围 [lower, upper] （包含 lower 和 upper）之内的 区间和的个数 。

区间和 S(i, j)表示在 nums 中，位置从 i 到 j 的元素之和，包含 i 和 j (i ≤ j)。

示例1：

输入：nums = [-2,5,-1], lower = -2, upper = 2
输出：3
解释：存在三个区间：[0,0]、[2,2] 和 [0,2] ，对应的区间和分别是：-2 、-1 、2 。

示例2：

输入：nums = [0], lower = 0, upper = 0
输出：1

提示：

  • 1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
  • − 2 31 < = n u m s [ i ] < = 2 31 − 1 -2^{31} <= nums[i] <= 2^{31} - 1 −231<=nums[i]<=231−1
  • − 1 0 5 < = l o w e r < = u p p e r < = 1 0 5 -10^5 <= lower <= upper <= 10^5 −105<=lower<=upper<=105
  • 题目数据保证答案是一个 32 位 的整数

2、基础框架

class Solution {
public:
    int countRangeSum(vector<int>& nums, int lower, int upper) {

    }
};

3、原题链接

327. 区间和的个数

二、解题报告

1、思路分析

  （1）如果暴力解决，时间复杂度为 O ( N 3 ) O(N^3) O(N3)，因为子数组的数量为 O ( N 2 ) O(N^2) O(N2)，而遍历验证这些子数组的和的时间复杂度为 O ( N ) O(N) O(N)，所以总的时间复杂度为 O ( N 3 ) O(N^3) O(N3)
  （2）优化1：利用前缀和数组，则不用遍历验证子数组的和，时间复杂度就变成 O ( N 2 ) O(N^2) O(N2)
  （3）优化2：任何一个子数组都会以某个位置结尾（常见思维模型），如果以 i i i 位置结尾的子数组达标的个数为 a a a 个，以 j j j 位置结尾的子数组达标的个数为 b b b 个，那么最终结果为每个位置结尾的子数组达标的个数之和（即先求以每个位置结尾的子数组和的达标个数）
  （4）如果 s u m ( i . . . j ) sum(i...j) sum(i...j) 累加和在 [lower, upper] 范围上，那么 s u m ( 0... j ) − s u m ( 0... i − 1 ) sum(0...j) - sum(0...i - 1) sum(0...j)−sum(0...i−1) 也在这个范围上。

举例：数组 arr(0…17)，要求的范围为 [10, 40]，那么如何求以 17 这个位置为结尾的子数组和落在 [10，40] 这个范围上的个数。

假设 arr(0…17) 的前缀和为 100，本质上就是在求必须以0开头有多少个前缀和落在 [100 - upper, 100 - lower] = [60, 90] 这个范围上，再一经转化就能得到以 17 位置为结尾的子数组。再具体点，sum(0…17) = 100，而sum(0…5) = 10，则可以反推出 sum(6…17) 的累加和 = 100 - 10 = 90，也就是说 arr[6] ~ arr[17] 这个子数组是达标的。

总结来说就是假设 0 ~ i i i 整体累加和是 x x x，题目的目标是 [ l o w e r , u p p e r ] [lower, upper] [lower,upper]，思路转化为求必须以 i i i 位置结尾的子数组累加和有多少个落在 [ l o w e r , u p p e r ] [lower, upper] [lower,upper] 范围上 等同于 必须从0出发有多少个前缀和在 [ x − u p p e r , x − l o w e r ] [x - upper, x - lower] [x−upper,x−lower] 上

原始数组 nums 处理成前缀和数组 sum，求 sum 数组中的每个数 x 之前有多少个数落在 [x - upper, x - lower] 范围上，怎么求呢？

假设数组为 [3, -2, 4, 3, 6, -1]，而目标范围是[1,5]。

准备一个结构，存放前缀和，一开始初始化时没有前缀和，可以在该结构中放一个0。

首先来到 0 位置，值为3，该位置为了达标，等同于要找它之前在结构中有几个数在[3 - 5, 3 - 1] = [-2, 2] 范围，在存放前缀和的结构中发现只有1个0，于是以0位置结尾的子数组达标个数为1，然后将当前的前缀和 sum = 3 放入到结构中。结构目前的值[0，3]；

接着来到 1 位置，当前前缀和sum = 3 + (-2) = 1，等同于在问结构中有多少个数在[1 - 5, 1 - 1] = [-4, 0] 范围，发现只有0，于是1位置达标的子数组个数为1，然后将当前的前缀和 1 加入到结构中。结构目前的值 [0，3，1];

接着来到 2 位置，当前前缀和 sum = 1 + 4 = 5，等同于在问结构中有多少个数在 [5 - 5, 5 - 1] = [0, 4] 范围，发现有3个（0,3,1)，所以以2位置结尾的子数组达标个数是3，然后将当前的前缀和 5 放入结构中。结构目前的值 [0，3，1，5];

以此类推。

那么这个结构应该具备什么样的性质呢？

  • 首先，这个结构能进行插入操作，此处插入的是整数；

  • 其次，该结构能提供一种查询：有多少个数字落在给定的 [a,b] 范围上；

  • 最后，该结构还必须能存放重复的数字。

假设某种结构中存储的数字全部按序组织且可以接受重复的数字，要支持从[a,b]的值的查询并不需要直接提供这种功能，只需要支持一种查询：小于某个key的数量。举例：要求[5,10]范围上的数字个数，先求小于5的数字个数 c 1 c1 c1，再求小于11的数字个数 c 2 c2 c2，则 c 2 − c 1 c2 - c1 c2−c1 就是 [5,10] 范围上的数字个数。

所以该问题实际就变成了这个结构要实现3个功能：
（1）可以存储重复数字；
（2）可以添加数字；
（3）可以查询小于key的数字个数。

这里就要提到一个问题：有序表不能接收重复的数字，在有序表上每个key都是不同的。那如果要使用有序表，该怎么办呢？

这个问题很好解决——将多个数字压在一起即可。增加一个数据项记录每个结点经过的数字个数，用压在一起的方式生成一棵树。

例如给定的数字是[5, 5, 3, 3, 3, 6, 6]，则依次形成的树为：
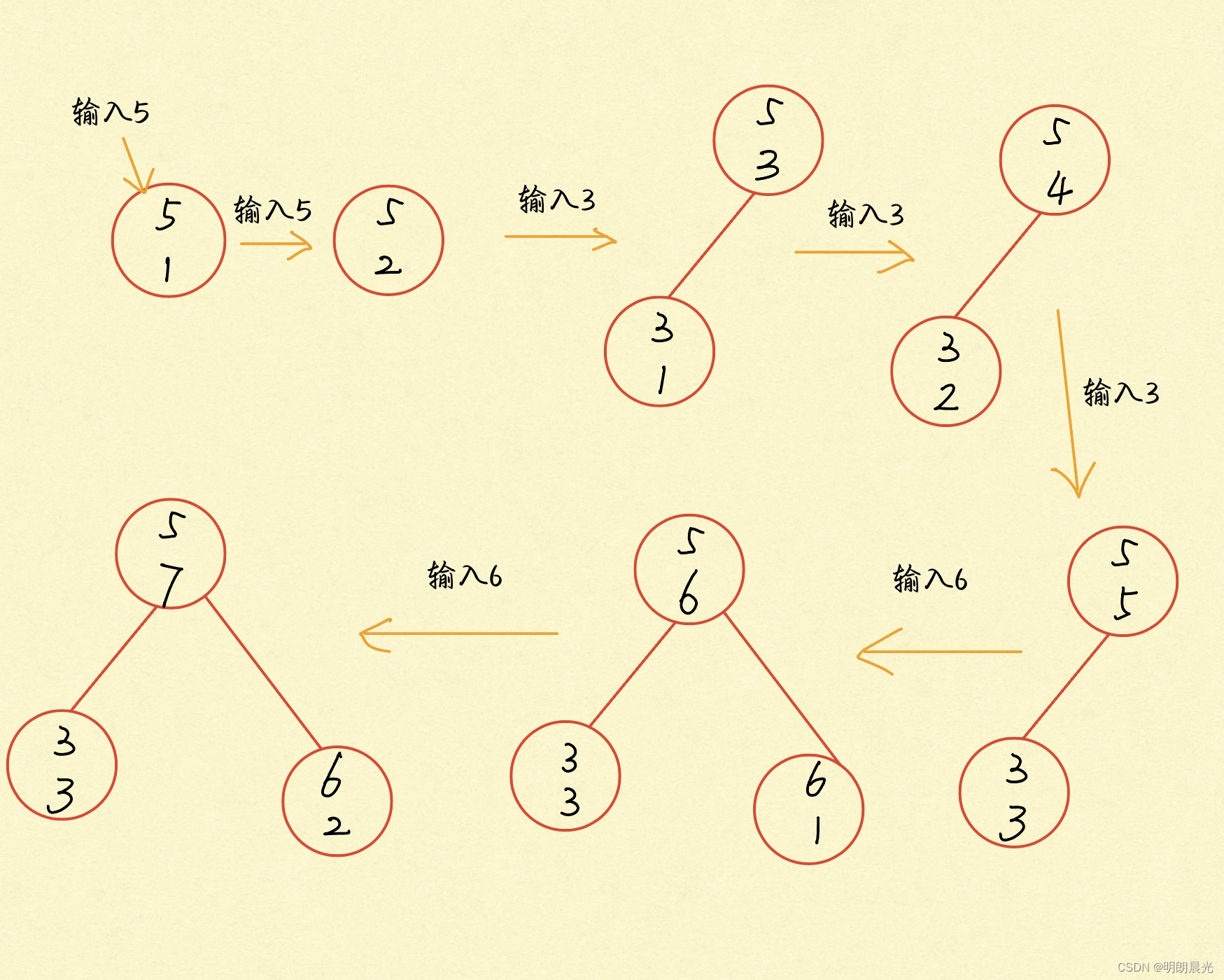
请添加图片描述
如何统计 5 的个数呢？在最后生成的树上，左树3个数，右树2个数，所以 5 的个数就是 7 − ( 3 + 2 ) = 2 7 - (3 +2) = 2 7−(3+2)=2 个。

这样的树就能支持查询小于key的数的个数，比如如下的树要查询 < 46 的值的个数：（往左不累加，往右才累加）
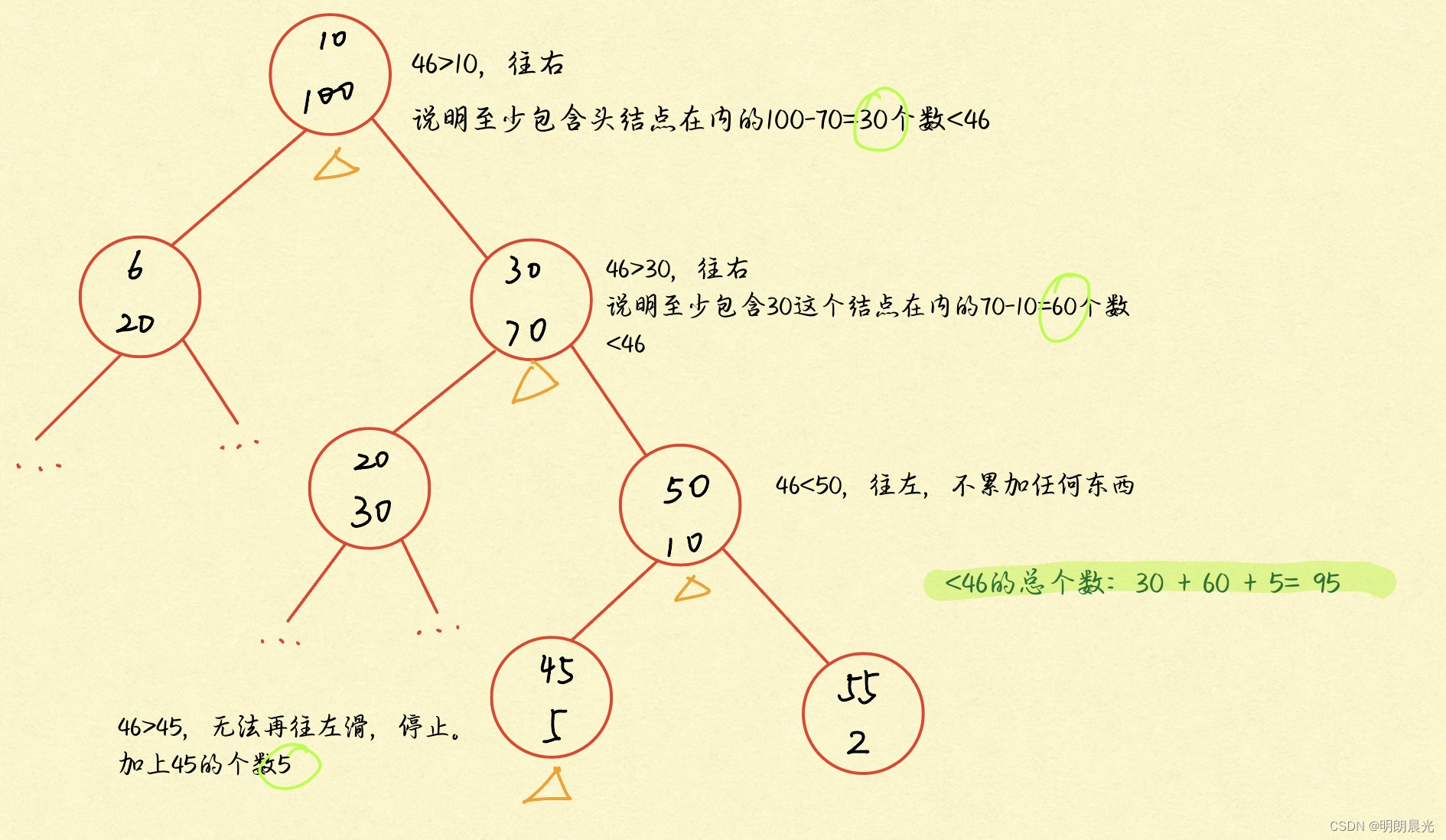
请添加图片描述

系统的有序表之所以没有做这个功能，是因为并不知道根据实际情况需要用到什么辅助数据项，如果不管应用场景，添加的若干数据项就会非常冗余。

至此，梳理下本题的脉络：要求的是整个数组中有多少个子数组的累加和落在 [ a , b ] [a,b] [a,b] 范围上，只要是子数组问题，满足某个S标准（此处就是累加和在 [ a , b ] [a,b] [a,b] 范围），通常的思路就是必须以 i i i 位置结尾的情况下有多少个子数组达标，进而做了一个转化，假设 0~ i i i 的累加和是 S S S，要想求子数组必须以 i i i 结尾的情况下，有几个子数组的累加和在 [ a , b ] [a,b] [a,b] 范围上，其实质就是在求 i i i 之前有多少个前缀和在 [ S − b , S − a ] [S-b, S-a] [S−b,S−a] 这个范围上。

进而想到了需要一个黑盒，这个黑盒可以放置所有的前缀和，且不去重，来到 i i i 位置的时候（假设到 i i i 位置的前缀和为S），如果之前的前缀和都在这结构中，且能查出在该结构中落在 [ S − b , S − a ] [S-b, S-a] [S−b,S−a] 范围的数量，对每个位置查询出来的结果相加就是全局的答案。

2、时间复杂度

O ( N l o g N ) O(N logN) O(NlogN)

3、代码详解

C++版

class Solution {
public:
    class SBTNode {
    public:
        long key;
        SBTNode *lchild;
        SBTNode *rchild;
        long size;
        long cnt;

        SBTNode(long k) : key(k), size(1), cnt(1), lchild(nullptr), rchild(nullptr) {}
    };

    class SizeBalancedTreeSet {
    private:
        SBTNode *root;
        unordered_set<long> hashSet;

        //右旋
        SBTNode *rightRotate(SBTNode *cur) {
            //cur的key重复的个数
            long same = cur->cnt - (cur->lchild ? cur->lchild->cnt : 0) - (cur->rchild ? cur->rchild->cnt : 0);

            //右旋
            SBTNode *leftNode = cur->lchild;
            cur->lchild = leftNode->rchild;
            leftNode->rchild = cur;

            //更新size
            leftNode->size = cur->size;
            cur->size = (cur->lchild ? cur->lchild->size : 0) + (cur->rchild ? cur->rchild->size : 0) + 1;

            //更新cnt
            leftNode->cnt = cur->cnt;
            cur->cnt = (cur->lchild ? cur->lchild->cnt : 0) + (cur->rchild ? cur->rchild->cnt : 0) + same;

            return leftNode;
        }

        //左旋
        SBTNode *leftRotate(SBTNode *cur) {
            long same = cur->cnt - (cur->lchild ? cur->lchild->cnt : 0) - (cur->rchild ? cur->rchild->cnt : 0);

            //左旋
            SBTNode *rightNode = cur->rchild;
            cur->rchild = rightNode->lchild;
            rightNode->lchild = cur;

            //更新size
            rightNode->size = cur->size;
            cur->size = (cur->lchild ? cur->lchild->size : 0) + (cur->rchild ? cur->rchild->size : 0) + 1;

            //更新cnt
            rightNode->cnt = cur->cnt;
            cur->cnt = (cur->lchild ? cur->lchild->cnt : 0) + (cur->rchild ? cur->rchild->cnt : 0) + same;

            return rightNode;
        }

        SBTNode *maintain(SBTNode *cur) {
            if (cur == nullptr) return nullptr;

            long leftSize = cur->lchild ? cur->lchild->size : 0;
            long leftLeftSize = cur->lchild && cur->lchild->lchild ? cur->lchild->lchild->size : 0;
            long leftRightSize = cur->lchild && cur->lchild->rchild ? cur->lchild->rchild->size : 0;

            long rightSize = cur->rchild ? cur->rchild->size : 0;
            long rightLeftSize = cur->rchild && cur->rchild->lchild ? cur->rchild->lchild->size : 0;
            long rightRightSize = cur->rchild && cur->rchild->rchild ? cur->rchild->rchild->size : 0;

            if (leftLeftSize > rightSize) { //LL
                cur = rightRotate(cur);
                cur->rchild = maintain(cur->rchild);
                cur = maintain(cur);
            } else if (leftRightSize > rightSize) { //LR
                cur->lchild = leftRotate(cur->lchild);
                cur = rightRotate(cur);
                cur->lchild = maintain(cur->lchild);
                cur->rchild = maintain(cur->rchild);
                cur = maintain(cur);
            } else if (rightRightSize > leftSize) { //RR
                cur = leftRotate(cur);
                cur->lchild = maintain(cur->lchild);
                cur = maintain(cur);
            } else if (rightLeftSize > leftSize) { //RL
                cur->rchild = rightRotate(cur->rchild);
                cur = leftRotate(cur);
                cur->lchild = maintain(cur->lchild);
                cur->rchild = maintain(cur->rchild);
                cur = maintain(cur);
            }
            return cur;
        }

        SBTNode *add(SBTNode *cur, long key, bool isExist) {
            if (cur == nullptr) {
                return new SBTNode(key);
            } else {
                //无论是否为存在的key，cnt都要更新
                cur->cnt++; 
                
                if (key == cur->key) { //已经存在的key，则直接返回
                    return cur;
                } else { //不存在的key，则新增节点挂到合适的位置
                    if (!isExist) {
                        cur->size++; //不同的key，size才会更新
                    } 

                    if (key < cur->key) {
                        cur->lchild = add(cur->lchild, key, isExist);
                    } else {
                        cur->rchild = add(cur->rchild, key, isExist);
                    }

                    return maintain(cur);
                }
            }
        }
    public:
        void add(long sum) {
            bool isExist = hashSet.count(sum) != 0;
            root = add(root, sum, isExist);
            hashSet.insert(sum);
        }

        // <key 的数字个数
        long lessKeySize(long key) {
            SBTNode *cur = root;
            long ans = 0;
            while (cur != nullptr) {
                if (key == cur->key) {
                    return ans + (cur->lchild ? cur->lchild->cnt : 0);
                } else if (key < cur->key) {
                    cur = cur->lchild;
                } else {
                    ans += cur->cnt - (cur->rchild ? cur->rchild->cnt : 0);
                    cur = cur->rchild;
                }
            }

            return ans;
        }

        // > key 的数字个数
        long moreKeySize(long key) {
            return root ? (root->cnt - lessKeySize(key + 1)) : 0;
        }
    };


    int countRangeSum(vector<int>& nums, int lower, int upper) {
        SizeBalancedTreeSet *treeSet = new SizeBalancedTreeSet();
        long sum = 0;
        int ans = 0;
        treeSet->add(0);
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];

            long a = treeSet->lessKeySize(sum - lower + 1);
            long b = treeSet->lessKeySize(sum - upper);

            ans += a - b;

            treeSet->add(sum);
        }
        delete treeSet;
        return ans;
    }
};

Java版

class Solution {
	public static class SBTNode {
		public long key; //参与排序的key
		public SBTNode l; //左孩子
		public SBTNode r; //右孩子
		public long size; // 不同key的size，是SBT的平衡因子
		public long all; // 总的size，上文提到的附加的数据项，记录经过每个结点的数字个数 （与平衡因子毫无关联）

		public SBTNode(long k) {
			key = k;
			size = 1;
			all = 1;
		}
	}

	public static class SizeBalancedTreeSet {
		private SBTNode root;
		private HashSet<Long> set = new HashSet<>();

		private SBTNode rightRotate(SBTNode cur) { //右旋
			long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
			SBTNode leftNode = cur.l;
			cur.l = leftNode.r;
			leftNode.r = cur;
			leftNode.size = cur.size;
			cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
			// all modify
			leftNode.all = cur.all; //数据项all也要变更
			cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;
			return leftNode;
		}

		private SBTNode leftRotate(SBTNode cur) { //左旋
			long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
			SBTNode rightNode = cur.r;
			cur.r = rightNode.l;
			rightNode.l = cur;
			rightNode.size = cur.size;
			cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
			// all modify
			rightNode.all = cur.all; //数据项all也要变更
			cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;
			return rightNode;
		}

		private SBTNode maintain(SBTNode cur) {
			if (cur == null) {
				return null;
			}
			long leftSize = cur.l != null ? cur.l.size : 0;
			long leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
			long leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
			long rightSize = cur.r != null ? cur.r.size : 0;
			long rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
			long rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
			if (leftLeftSize > rightSize) {
				cur = rightRotate(cur);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			} else if (leftRightSize > rightSize) {
				cur.l = leftRotate(cur.l);
				cur = rightRotate(cur);
				cur.l = maintain(cur.l);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			} else if (rightRightSize > leftSize) {
				cur = leftRotate(cur);
				cur.l = maintain(cur.l);
				cur = maintain(cur);
			} else if (rightLeftSize > leftSize) {
				cur.r = rightRotate(cur.r);
				cur = leftRotate(cur);
				cur.l = maintain(cur.l);
				cur.r = maintain(cur.r);
				cur = maintain(cur);
			}
			return cur;
		}

		private SBTNode add(SBTNode cur, long key, boolean contains) {
			if (cur == null) {
				return new SBTNode(key);
			} else {
				cur.all++; //加入新的key的时候，无论该key是否存在，all都要++，
				if (key == cur.key) {
					return cur;
				} else { // 还在左滑或者右滑
					if (!contains) {
						cur.size++; //只有当之前不存在的key增加时，size才会增加
					}
					if (key < cur.key) {
						cur.l = add(cur.l, key, contains);
					} else {
						cur.r = add(cur.r, key, contains);
					}
					return maintain(cur);
				}
			}
		}

		public void add(long sum) {
			boolean contains = set.contains(sum);
			root = add(root, sum, contains);
			set.add(sum);
		}

		//只和二叉搜索树有关，和平衡性无关
		public long lessKeySize(long key) { //<key的个数
			SBTNode cur = root;
			long ans = 0;
			while (cur != null) {
				if (key == cur.key) { //要的是<key的值，获取左子树上的all
					return ans + (cur.l != null ? cur.l.all : 0);
				} else if (key < cur.key) { //往左划，不获得
					cur = cur.l;
				} else { //往右划，则至少该结点及该结点的左子树上的数都是<key的即该结点的all - 右树的all
					ans += cur.all - (cur.r != null ? cur.r.all : 0);
					cur = cur.r;
				}
			}
			return ans;
		}

		// > 7 8...
		// <8 ...<=7
		public long moreKeySize(long key) {
			return root != null ? (root.all - lessKeySize(key + 1)) : 0;
		}
	}

    public int countRangeSum(int[] nums, int lower, int upper) {
		// 黑盒：加入数字（即前缀和）；不去重，可以接受重复数字；可以查询 <num 有几个数
		SizeBalancedTreeSet treeSet = new SizeBalancedTreeSet();
		long sum = 0;
		int ans = 0;
		treeSet.add(0);// 一个数都没有的时候，就已经有一个前缀和累加和为0，
		for (int i = 0; i < nums.length; i++) { //必须以 i 结尾的情况下子数组达标的数量
			sum += nums[i];
			// 目标转换为求i之前有多少个前缀和落在[sum - upper, sum - lower]范围上
			// 如想查询前缀和在[10, 20]范围的个数
			// 本质上是在查询 <10 和 <21 的个数各是多少，然后用<21的数量 - <10的数量，就是前缀和在[10,20]这个范围的个数
			long a = treeSet.lessKeySize(sum - lower + 1);
			long b = treeSet.lessKeySize(sum - upper);
			ans += a - b;
			treeSet.add(sum);//当前的前缀和放到结构中
		}
		return ans;
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/357427.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于jsplumb构建的流程设计器

基于jsplumb构建的流程设计器

项目背景 最近在准备开发工作流引擎相关模块&#xff0c;完成表结构设计后开始着手流程设计器的技术选型&#xff0c;调研了众多开源项目后决定基于jsplumb.js开源库进行自研开发&#xff0c;保证定制化的便捷性&#xff0c;相关效果图及项目地址如下 项目地址&#xff1a;ht…
阅读更多...
进程切换-

进程切换-

实验课之前有一些问题 中断机制 第一个问题&#xff1a; interrupt的两个状态源头&#xff1a; 外中断多由随机中断&#xff08;异步中断&#xff09;造成&#xff0c;如鼠标点击&#xff0c;键盘输入&#xff1b; 内终端多由故障终端&#xff1a;程序运行异常&#xff0c;硬件…
阅读更多...
使用PyQtGraph 自定义绘图

使用PyQtGraph 自定义绘图

Python 的主要优势之一是探索性数据科学和可视化生态体系。一般的工具链为Pandas、numpy、sklearn 进行数据分析和使用matplotlib进行绘图。 但是如果需要自己自定义一个个性化的图形界面工具&#xff0c;则可能不是很合适。为了实现这种需求&#xff0c;可以使用PyQt构建GUI应…
阅读更多...
【进阶篇】线程的硬件基础

【进阶篇】线程的硬件基础

文章目录高速缓存缓存一致性协议写缓冲区和无效化队列高速缓存 简介 高速缓存是主内存与处理器之间的硬件&#xff0c;其容量小于主存&#xff0c;但存取速率远高于主存。因此处理器在执行读写操作时&#xff0c;可直接和高速缓存交互&#xff0c;提高响应速度。 我们常见的变…
阅读更多...
2049. 统计最高分的节点数目

2049. 统计最高分的节点数目

2049. 统计最高分的节点数目题目算法设计&#xff1a;深度优先搜索题目 传送门&#xff1a;https://leetcode.cn/problems/count-nodes-with-the-highest-score/ 算法设计&#xff1a;深度优先搜索 这题的核心是计算分数。 一个节点的分数 左子树节点数 右子树节点数 除自…
阅读更多...
【Opencv 系列】 第4章 直方图

【Opencv 系列】 第4章 直方图

文章目录[TOC](文章目录)前言1、直方图的定义、意义、特征2、直方图&#xff1a;2.1 灰度直方图2.2 彩色直方图前言 1、直方图的定义、意义、特征 在统计学中&#xff0c;直方图是一种对数据分布情况的图形表示&#xff0c;是一种二维统计图表&#xff0c;他的两个坐标分别是统…
阅读更多...
docker安装配置镜像加速器-拉取创建Mysql容器示例

docker安装配置镜像加速器-拉取创建Mysql容器示例

List item docker 常见命令大全docker安装docker拉取创建Mysql容器docker 安装 1、安装链接&#xff1a;https://blog.csdn.net/BThinker/article/details/123358697 &#xff1b; 2、安装完成需要配置docker镜像加速器 3、docker 镜像加速器推荐使用阿里云的&#xff1a; 编…
阅读更多...
硬件学习 软件Cadence day04 PCB 封装绘制

硬件学习 软件Cadence day04 PCB 封装绘制

1.文章内容&#xff1a; 1. 贴片式电容 PCB 封装绘制 &#xff08;型号 c0603 &#xff09; 2. 贴片式电阻 PCB 封装绘制 &#xff08;型号 r0603 &#xff09; 3. 安规式电容 PCB 封装绘制 &#xff08;这个就是 有一个电容&#xff0c;插入一个搞好的孔里面 …
阅读更多...
社区宠物诊所管理系统

社区宠物诊所管理系统

目录第一章概述 PAGEREF _Toc4474 \h 21.1引言 PAGEREF _Toc29664 \h 31.2开发背景 PAGEREF _Toc3873 \h 3第二章系统总体结构及开发 PAGEREF _Toc19895 \h 32.1系统的总体设计 PAGEREF _Toc6615 \h 32.2开发运行环境 PAGEREF _Toc13054 \h 3第三章数据库设计 PAGEREF _Toc2852…
阅读更多...
Prometheus 告警机制介绍及命令解读

Prometheus 告警机制介绍及命令解读

本文您将了解到Prometheus 告警模块Alertmanager的架构介绍、核心概念、命令解析和AMTool的基本使用。 Prometheus的告警模块并不存在于Prometheus中，而是 以独立项目Alertmanager存在。Prometheus服务器定义告警规则，这些规则将触发警报，将警报发送到Alertmanager。Alertma…
阅读更多...
DaVinci 偏好设置：系统 - 解码选项

DaVinci 偏好设置：系统 - 解码选项

偏好设置 - 系统/解码选项Preferences - System/Decode Options解码选项Decode Options使用 GPU 进行 Blackmagic RAW 解码Use GPU for Blackmagic RAW decode允许使用 GPU 来加速 Blackmagic RAW&#xff08;BRAW&#xff09;媒体的解码。使用硬件加速解码 H.264/H.265Decode …
阅读更多...
谁再用Double定义存储计算金额，我劈了他

谁再用Double定义存储计算金额，我劈了他

不是三婶儿偏执&#xff0c;非要吐槽。家人们&#xff0c;咱就是说&#xff0c;按照基操逻辑谁会把严格金额计算相关的数据使用double类型呢… “我以为吕布已经够勇猛了&#xff0c;这是谁的部下&#xff1f;” 前几天&#xff0c;一同事让帮忙写段代码。内容比较常规&#xf…
阅读更多...
Unity之ASE实现边缘光效果

Unity之ASE实现边缘光效果

一.前言 今天来实现一个简单的边缘光效果&#xff0c;可以应用与物体表面的一种荧光外溢的效果&#xff0c;特别是用在人的身体表面&#xff0c;会让人的皮肤更细腻&#xff0c;更好看。 物体上效果如下: 人体表面效果如下&#xff1a; 我们可以看到&#xff0c;这种人体表面…
阅读更多...
Redis的整合和使用

Redis的整合和使用

引入依赖 <!--整合redis--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency>添加配置 spring.redis.host127.0.0.1 spring.redis.port6379 spring.…
阅读更多...
算法训练营 day49 动态规划 爬楼梯 （进阶）零钱兑换 完全平方数

算法训练营 day49 动态规划 爬楼梯 （进阶）零钱兑换 完全平方数

算法训练营 day49 动态规划 爬楼梯 &#xff08;进阶&#xff09;零钱兑换 完全平方数 爬楼梯 &#xff08;进阶&#xff09; 70. 爬楼梯 - 力扣&#xff08;LeetCode&#xff09; 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同…
阅读更多...
PPO（proximal policy optimization）算法

PPO（proximal policy optimization）算法

博客写到一半发现有篇讲的很清楚&#xff0c;直接化缘了 https://www.jianshu.com/p/9f113adc0c50 Policy gradient 强化学习的目标&#xff1a;学习到一个策略πθ(a∣s)\pi\theta(a|s)πθ(a∣s)来最大化期望回报。 一种直接的方法就是在策略空间中直接搜索来得到最优策略&…
阅读更多...
详解Ansible中角色的使用

详解Ansible中角色的使用

目录 一、ansible roles 1、ansible 角色简介 2、roles目录结构 3、role存放的路径在配置文件ansible.cfg中定义 4、创建目录结构 二、roles的写法及应用 1、覆盖变量 2、控制任务执行顺序 三、ansible—galaxy命令工具 一、ansible roles 1、ansible 角色简介 * Ans…
阅读更多...
VNCTF 2023复现

VNCTF 2023复现

文章目录象棋王子电子木鱼BabyGo象棋王子 签到题&#xff0c;直接在源码中找就ok。 找到一处编码&#xff0c;在控制台输出。 flag为&#xff1a;flag{w3lc0m3_t0_VNCTF_2023~~~} 电子木鱼 需要先理清代码逻辑。 存在三个路由。 一&#xff1a;/路由用来查看当前的功德数量…
阅读更多...
兼职任务平台收集（二）分享给有需要的朋友们

兼职任务平台收集（二）分享给有需要的朋友们

互联网时代&#xff0c;给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说&#xff0c;网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金&#xff0c;这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…
阅读更多...
Git详解

Git详解

Git1.Git简介1.1 Git是什么1.2 Git的作用1.3 Git的简介1.4 Git的下载和安装1.5 Git的安装目录结构如下2.Git代码托管服务2.1 常用的Git代码托管服务1.Git简介 1.1 Git是什么 Git是一个分布式版本控制工具&#xff0c;主要用于管理开发过程中的源代码文件&#xff08;Java类、x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023