2049. 统计最高分的节点数目

• • 题目
  • 算法设计：深度优先搜索

 

---

题目

传送门：https://leetcode.cn/problems/count-nodes-with-the-highest-score/

 

---

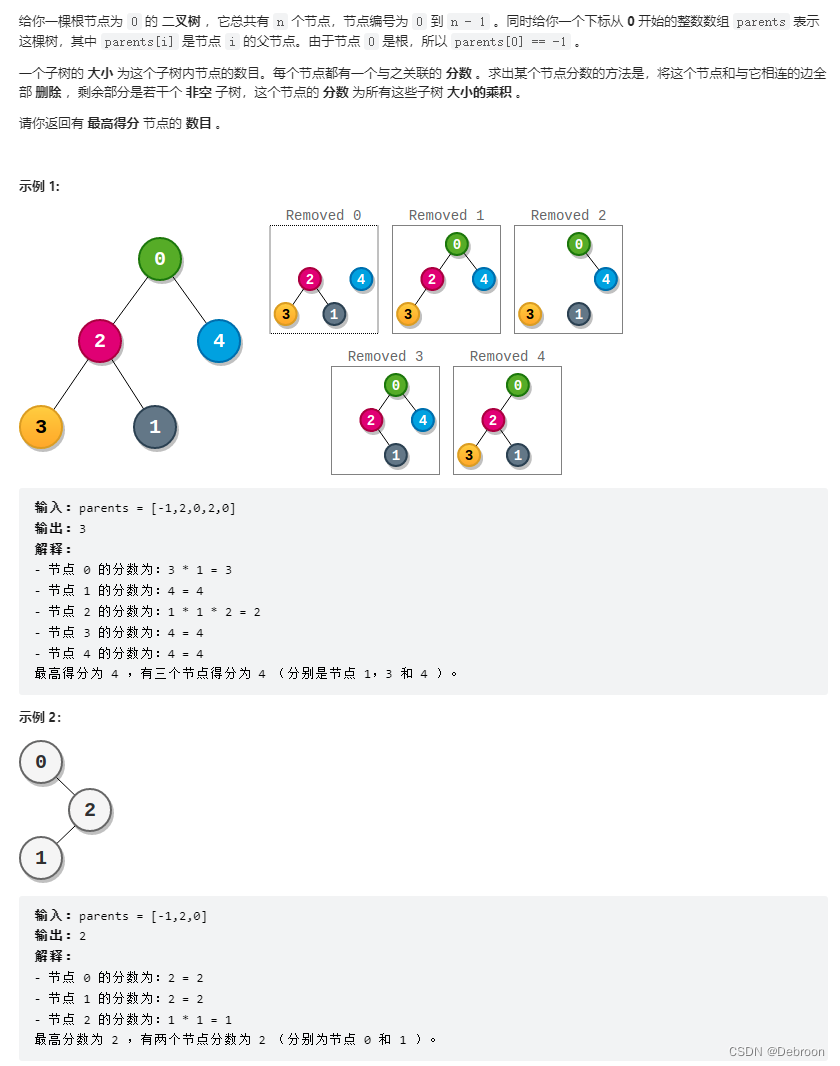
算法设计：深度优先搜索

这题的核心是计算分数。

一个节点的分数 = 左子树节点数 × 右子树节点数 × 除自己外其他节点数。如下图：

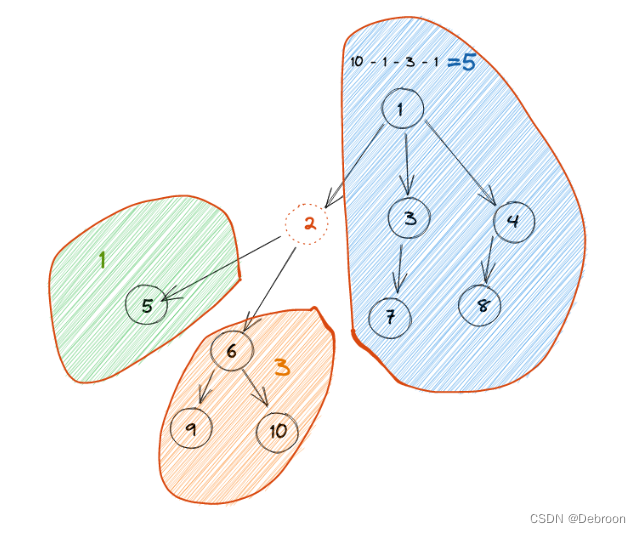
删除某个节点之后，最多会把二叉树分割成 三个部分 ：左子树、右子树、父节点及父节点的另一半子树（除自己外其他节点个数）。

使用 DFS 算出左子树节点数、右子树节点数。

因为知道树节点的总数，再计算除自己外其他节点个数。

• 除自己外其他节点个数 = 总数 - 1 - 左子树节点数 - 右子树节点数。

具体怎么解呢？

一个节点的分数 = 左子树节点数 × 右子树节点数 × 除自己外其他节点数

• 一是，需要清晰左子树节点数、右子树节点数，再通过总数 - 左右子树数 - 1，得到除自己外其他节点数

• 二是，三个数量都有了之后，相乘就是删除这个节点之后的分数，当然，这里有可能三个部分中缺失一部分或者两部分，缺失的部分用 1 来代替去相乘。

• 最终表达式：一个节点的分数 = 左子树节点数 × 右子树节点数 × (总数 - 左右子树数 - 1)

int dfs(vector<vector<int>> &tree, vector<long> &s, int i) { 
	long score = 1, sum = 1;                                       // 分数，节点总数，设置为long防止溢出
	for (int j : tree[i]) {                                        // 遍历i所有子节点
		int cnt = dfs(tree, s, j);                                 // 得出子树节点个数
		score *= cnt, sum += cnt;                                  // 计算左右子树的得分，同时计算节点总数，累计每个子树节点数量和。因为分数等于三块的乘积，可同时计算节点数量、分数
	} 
	s[i] = score * (max(1ll, (long)tree.size() - sum));            // 一个节点分数 = 左子树节点数 × 右子树节点数 × (总数 - 左右子树数 - 1)。1ll是把1改成long long类型
	return i != 0 ? sum : count(begin(s), end(s), *max_element(begin(s), end(s)));    // *max_element查询最大分数，count统计最大分数的个数
} 
int countHighestScoreNodes(vector<int>& parents) {                 // 题目给的 parents 数组不是树，先建树
	int n = parents.size();
	vector<vector<int>> tree(n);                                   // 用数组存储树
	vector<long> s(n); 
	for (int i = 1; i < n; ++i) tree[parents[i]].push_back(i);     // 根据parents建树，tree[i]存储i的子节点
	return dfs(tree, s, 0);                                        // 在图上dfs计算分数
}