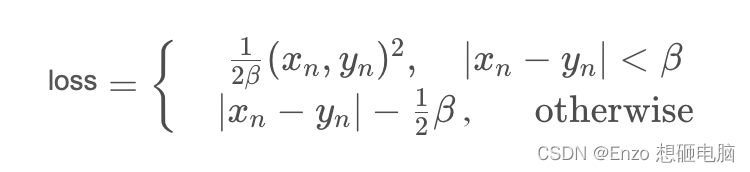在实际应用的时候,我们的样本不会是完全干净的,即存在噪声样本。那使用存在噪声的样本时,我们如何更有效的进行模型学习呢?

Label Dependent Nose
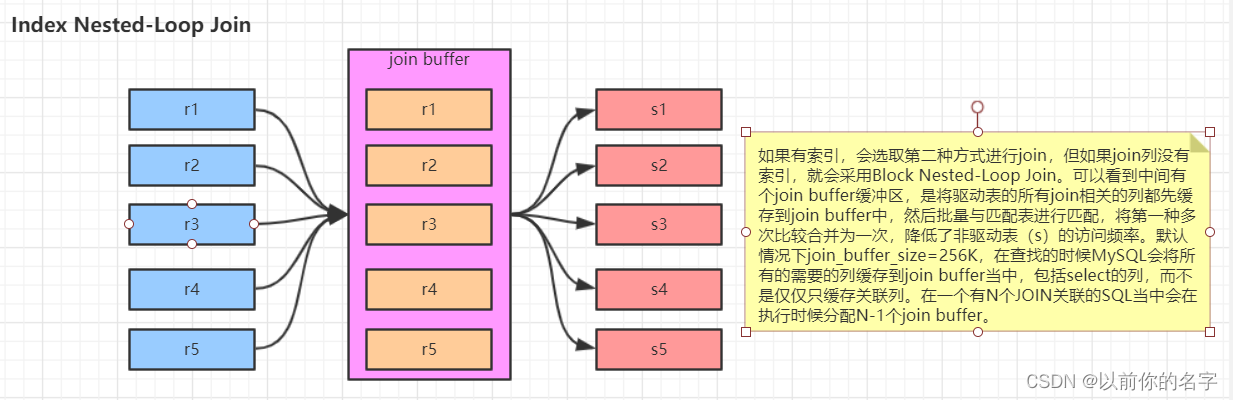
样本选择(Sample Selection)
第一种很直接的想法,就是我们在样本集里,把那些‘噪声’找出来,然后直接过滤掉。但这里面的难点在于怎么找出哪些噪声。
人工经验:比如大学生一般是18岁-30之间,如果小于18岁,比如只有15岁就大概率不是。
规则:比如先走一遍已存在的比较靠谱的模型,将p比较低的直接过滤;
另一种想法,就是在模型训练的时候,进行样本选择。即对于每个batch,只选择clean样本的loss进行模型的更新。其中比较主流的方法时co-train系列。

Decoupling(《Decoupling “when to update” from “how toupdate”》)
核心思路:分别独立训练2个模型,对于每个batch,2个模型分别预测。对于预测结果不一致的数据,才会被选择用来更新模型的参数,又被称为「update by disagreement」
Co-teaching(《Co-teaching: Robust Training of Deep Neural Networks with Extremely Noisy Labels》)
核心思路:对于2个模型f和g。对于每个batch,选择模型f中loss比较小的数据,计算这些数据在模型g上的损失并更新模型g的参数。同时选择模型g中loss比较小的数据,计算它们在f上的损失并更新模型f的参数。每个batch里选择多少个数据,由R(T)来控制。
Co-teaching+(ICML2019的《How does Disagreement Help Generalization against Label Corruption?》)
核心思路: 结合了Co-teach和decoupling的思路
正则化(Robust Regularization)
通过正则化的方法,防止模型过拟合岛噪声样本上。比如Dropout、BN等方法。
显式正则:比如Dropout、BN、权重衰减等。这里介绍一种bilevel learning
bilevel learning:使用一个干净的验证集,应用双层优化的方式来约束过拟合。通过调整权重,最小化在验证集上的错误。在每个mini-batch上,计算训练样本和验证集样本之间梯度的一致性,一致性高的训练样本对应的权重增大。
隐式正则:在不降低模型表示能力的前提下提升了泛化性能
adversarial training: 对抗训练,鼓励网络正确分类原始输入和扰动的输入;
label smoothing:标签平滑,防止过度自信,平滑分类边界,平滑标签是原始标签和其他可能标签的加权组合;
mixup: 数据线性插值,标签也线性插值
结构设计(Robust Architecture)
噪声自适应层(noise adaptation layer)
专门用噪声过渡矩阵来建模噪声转换,测试的去掉这一层。只针对实例无关的噪声。
Loss设计(Robust Loss)
首先我们介绍下对称损失(Symmetric Loss),因为Symmetric Loss是理论可证明噪声鲁棒的。
我们这里考虑2分类任务。对于训练样本x,标签为y(y ∈ {0, 1}),fθ(x)为模型输出(θ为待优化的参数),损失函数为l。
a. 没有标签噪声的情况下,待优化的目标为l[fθ(x), y] (1);
b. 在考虑有噪声的情况下,x有概率ρ被误标为1-y,那么实际上的优化目标是(1−ρ)⋅l[fθ(x), y] + ρ⋅l[fθ(x), 1−y] (2)。
c. 对于目标函数(2),如果无论有无噪声,该优化问题都会得到同样的解。这时候损失函数L就是噪声鲁棒的。
d. 目标函数(2)可以转换为如下,整理后的第一项是目标函数(1)的一个固定倍数。而第二项是当样本标签等概率取遍所有可能值时,所产生的损失值。

e. 如果满足如下结果时(其中C是常数),那么l就是Symmetric Loss,即优化目标函数(2)和优化目标函数(1)是等价的。

MAE
考虑2分类,l[fθ(x), y] + l[fθ(x), 1-y] = |1-fθ(x)| + |0-fθ(x)| = 1,所以MAE是对称损失。但MAE的性能比较差,跟CCE(categorical cross entropy)相比,训练的收敛时间更长。
GCE(generalized cross entropy)
CE/CCE不是对称损失。l[fθ(x), y] + l[fθ(x), 1-y]=C,要求各个损失项非负,且其和为定值,那么各个损失项必然是有界的。但在当fθ(x)接近于0或者1时,logfθ(x)或−log(1−fθ(x))是无界的。

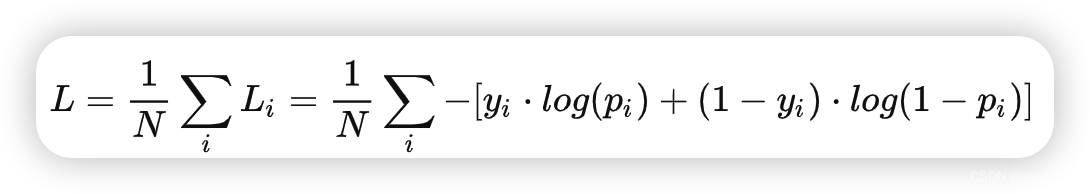
GCE可以兼顾MAE的鲁棒性和CE的性能。−log(fθ(x))项,替换成一个指数项

其中幂次q为一个超参数,取值范围为(0, 1] 。当q = 1时,该指数项就蜕变为MAE的形式;当q→0时,由洛必达法则,该指数项将蜕变为CE的形式。
SCE(symmetric cross entropy):在CCE上结合了一个noise tolerance term。

Focal Loss & GHM Loss
GHM可以认为是Focal Loss的一种优化。如下图所示,梯度模长在接近0时样本量最多,这部分是简单样本。随着模长增大,样本量迅速下降,在U字底部的部分可以认为是困难样本。在模长接近1时,数量又变多,这部分可以认为是极困难样本或者噪声样本。
最终根据这种分布设计梯度密度,来调整样本的权重。

Loss Adjustment
Loss Correction:和噪声自适应层类似,损失校正通过给模型输出结果乘上一个估计的标签转移矩阵来修改loss,不同之处在于,噪声转移矩阵的学习是和模型的学习解耦的。包括backward correction、forward correction等。
Loss Reweighting:计算loss时给假样本更小的权重,给真样本更高的权重。这类方法手动设计权重函数和超参。
Label Refurbishment:将网络的输出标签和噪声标签组合作为翻新后的标签:(a是噪声标签的置信度)

Meta Learning
Instance Dependent Noise
实际上在真实世界的数据集中,存在更多的是instance-dependent (feature-dependent) label noise,即特征相关的噪音标签。
SEAL(self-evolution average label)
CORES(COnfidence REgularized Sample Sieve)
参考
Learning from Noisy Labels with Deep NeuralNetworks: A Survey