参考

项目	描述
关于物理像素、逻辑像素（css像素）、分辨率、像素比的超详细讲解	古达星球
设备像素比（devicePixelRatio）	xueli_2017
百度百科	查询
搜索引擎	[Bing](必应 (bing.com))

描述

项目	描述
操作系统	Windows 10 专业版
Edge	110.0.1587.41 (正式版本) (64 位)
物理分辨率	1920 * 1080

像素

设备将图像显示到屏幕中，是以一个个小方格为单位对图像进行绘制的，这些小方格便是像素点，也即像素。

分辨率

显示分辨率

显示分辨率是指显示器在显示图像时的分辨率。通常以显示器的一行像素数乘一列像素数的表达式来表示显示器的分辨率，例如：

显示分辨率 1980x1024 表示显示器的每一行可以容纳 1980 个像素点，每一列可以容纳 1024 个像素点，显示屏共可容纳 2027520 个像素点。

图像分辨率

图像分辨率即图像中存储的信息量，通常以图像每一行所包含的像素点信息（颜色值，透明度等信息）的数量乘每一列所包含的像素点信息的数量的表达式来表示图像分辨率。

图像分辨率即图像中存储的信息量，在图像分辨率不变的情况下，你若对图像进行放缩操作，相关系统将做出如下行为：

1. 在你对图像进行放大操作时，系统将通过相关算法对其进行像素补充。

2. 在你对图像进行缩小操作时，系统将通过相关算法对其进行像素剔除。

物理分辨率

物理分辨率描述了设备可用于显示的格子数，在设备的生产过程中就已经被确定。物理分辨率决定了某一设备所能够支持的最大显示分辨率。

分辨率单位（仅部分）

除了使用 一行像素点数 乘 一列像素点数 的表达式来表示分辨率外，还可以使用分辨率单位来表示分辨率的大小。

DPI

DPI 即 DOTS PER INCH（每英寸点数），该单位描述了每英寸距离含有多少个打印点。像素单位 DPI 常用于印刷领域。

PPI

PPI 即 Pixels Per Inch （每英寸像素数），该单位描述了每英寸距离含有多少个像素点。

设备像素比

设备物理像素

设备物理像素在设备的生产过程中就已被指定，单位为 pt 。你可以使用 1pt * 1pt 表示设备用于显示像素的物理格子的大小。

设备独立像素

设备独立像素即定义 UI 布局时所使用到的虚拟像素单位，在网页设计过程中使用到的 px 等单位就是设备独立像素中的一种。程序在遇到设备独立像素时，将通过一定的规则（设备像素比）将其转换为设备物理像素。

设备像素比

产生

由于屏幕尺寸及分辨率的不同，同样分辨率大小的图片将以不同尺寸的物理大小（厘米，米等单位计量）展示在设备中，这会影响客户的体验。

举个栗子

在分辨率为 375*667 的设备中，12px 大小的文字显示效果如下：

而在分辨率为 750*1334 的设备中，12px 大小的文字的显示效果为：

为了减小屏幕尺寸及分辨率对网页页面的显示带来的影响，设备像素比应运而生。

设备像素比

设备像素比与设备物理像素及设备独立像素的关系为：

设备像素比 = 设备物理像素 / 设备独立像素

设备像素比为设备独立像素到设备物理像素的转换提供了依据。以 iPhon SE 为例，其物理分辨率为 750*1334 ，而其默认的设备像素比为 2，因此 iPhone SE 显示网页内容时，将使用 2pt 设备物理像素显示 1px 设备独立像素的所包含的内容，显示内容的物理大小（厘米，米等物理单位）与相同设备尺寸但分辨率为 375 * 667 的设备无异。

放大与缩小

网页的放大与缩小改变的内容其实是当前页面（当前页面的放大或缩小并不会影响该浏览器的其他标签页）所使用的设备像素比，放大页面将增大设备像素比，缩小页面将减小设备像素比。

在 JavaScript 中，你可以使用如下代码输出当前设备在当前页面下使用的设备像素比。

console.log(window.devicePixelRatio);

在浏览器的控制台（位于浏览器的开发者工具中）中，你可以直接使用 window.devicePixelRatio 来输出当前设备在当前页面使用的设备像素比。

举个栗子

可以看到，我的浏览器使用的默认设备像素比为 1.25 。现在，我将对该页面缩放至 200% 。缩放完毕后，我们再次观察其设备像素比。

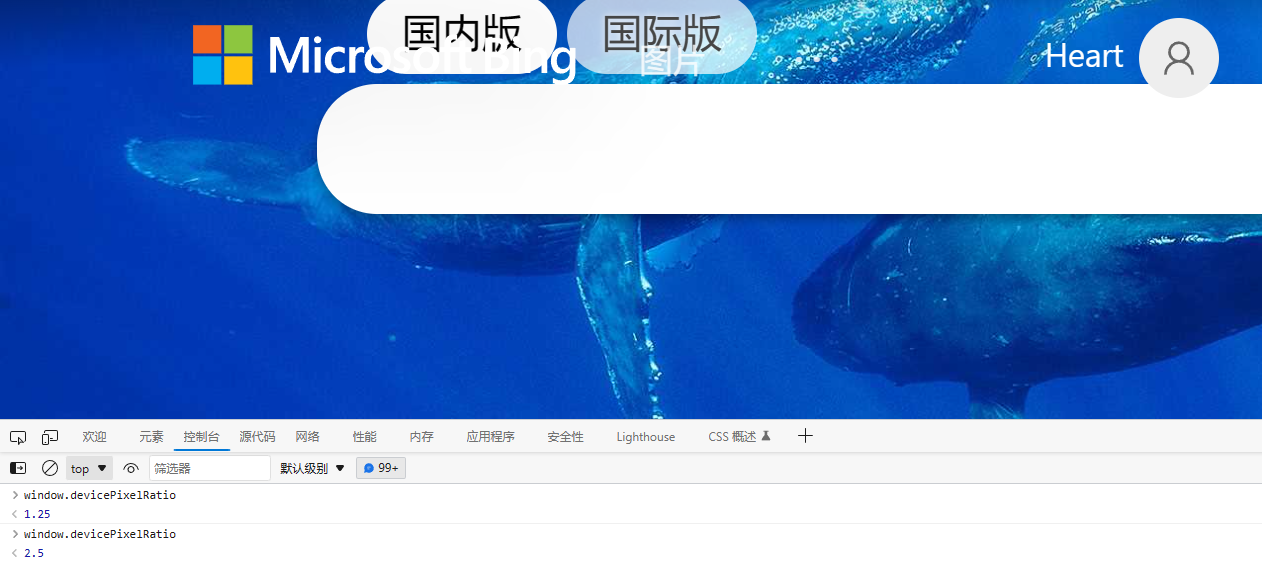
可以看到，在页面放大了两倍后，设备像素比也放大了两倍。

尾声

💕欢迎建议💕 如果你对这篇博客右什么意见，欢迎指出。

💞欢迎提问💞 如果各位对文章中的某些内容不太理解，欢迎提问。