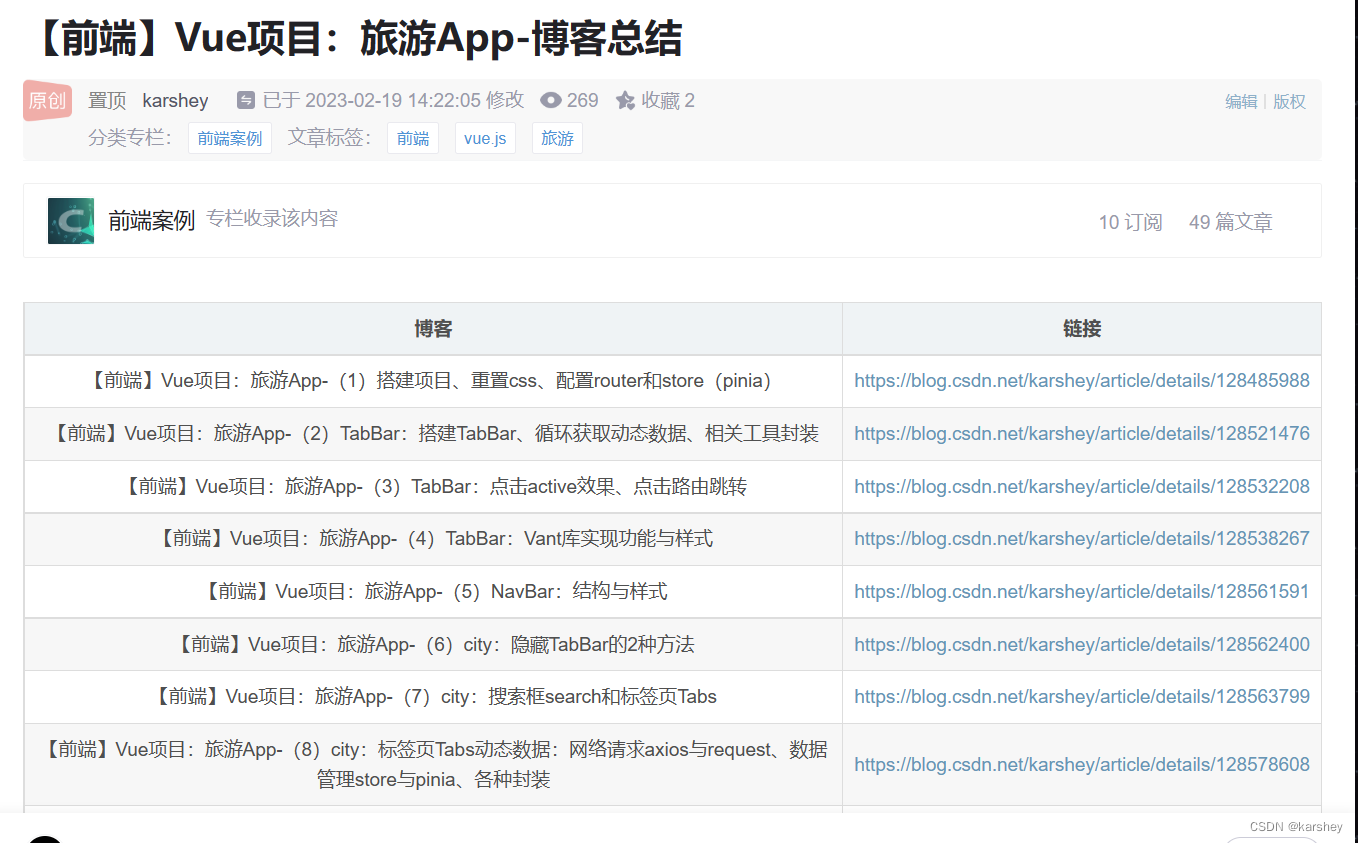
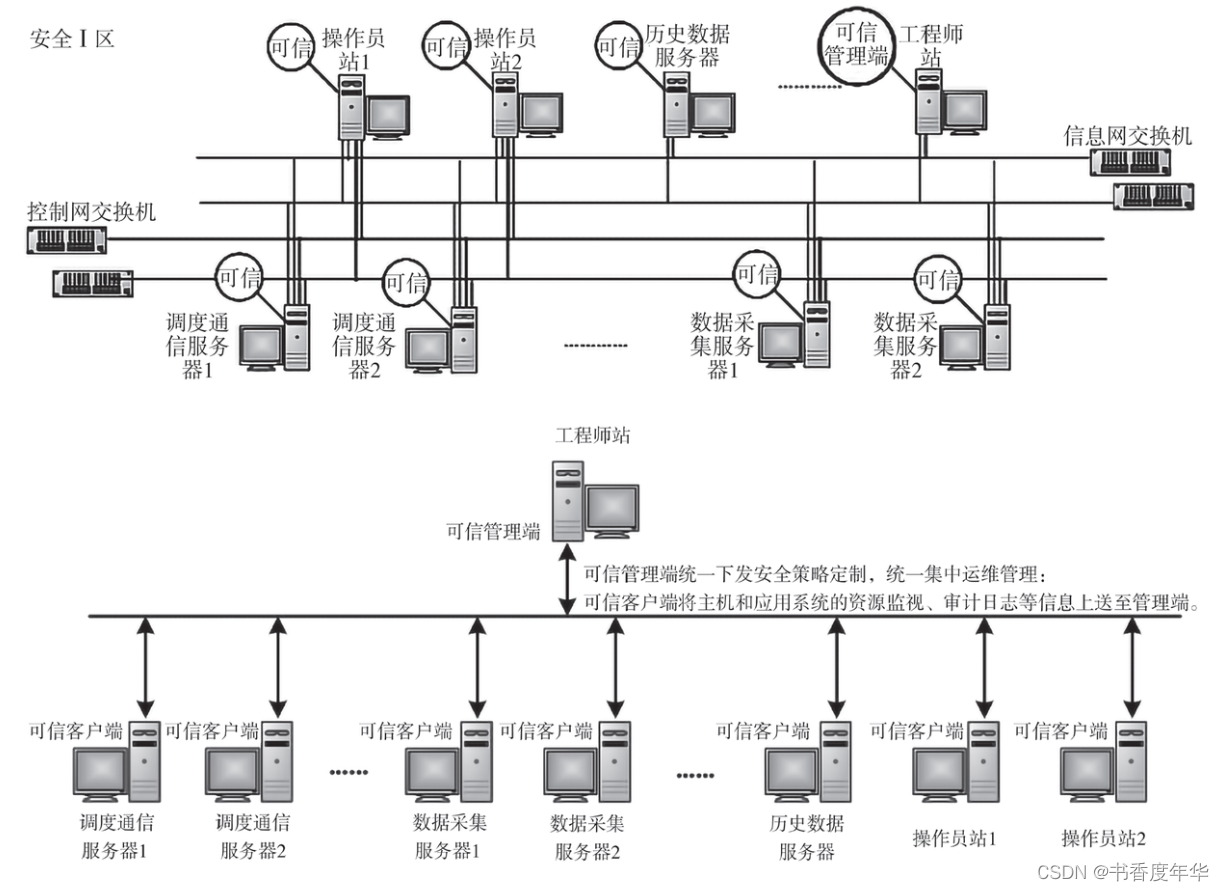
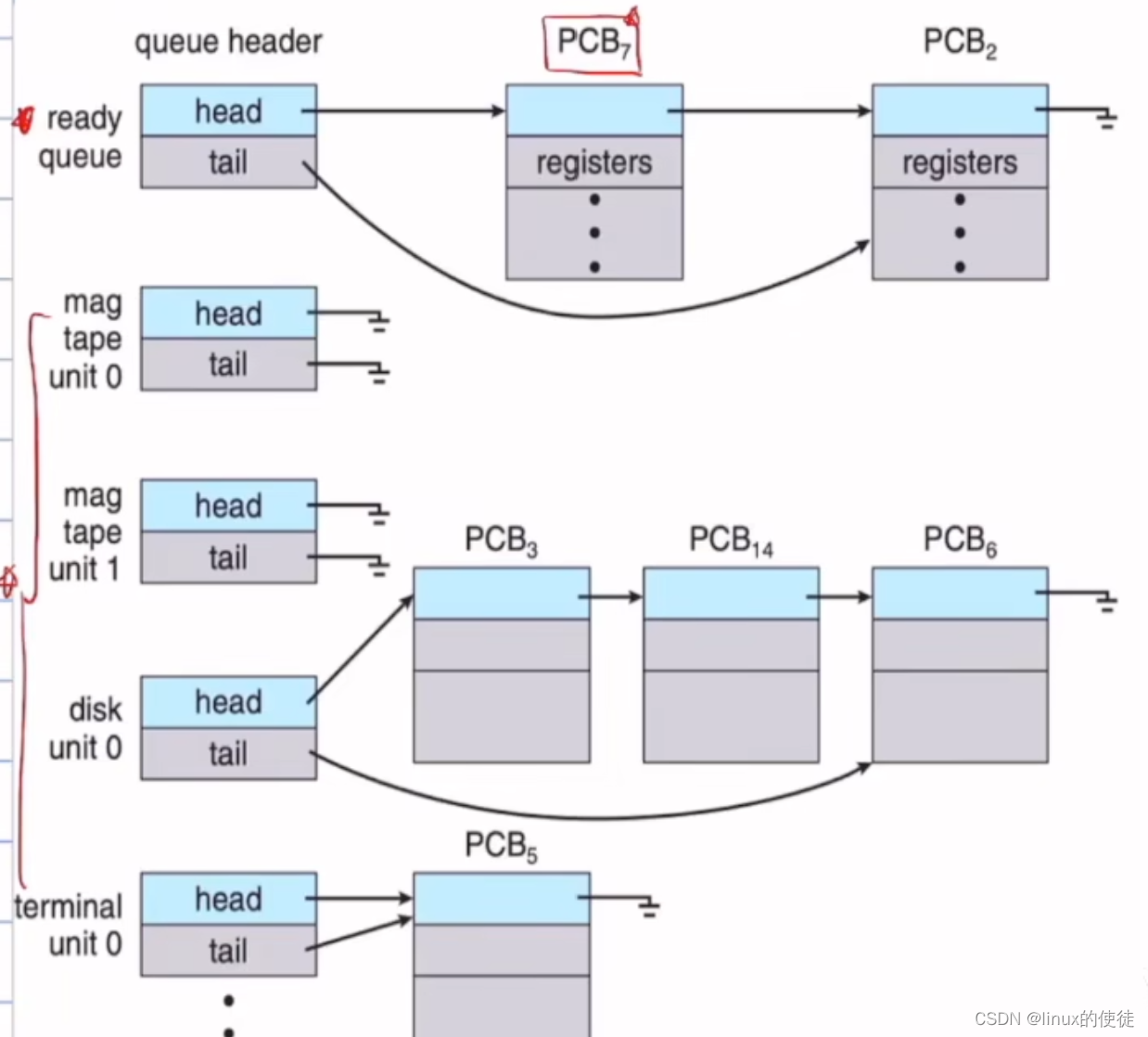
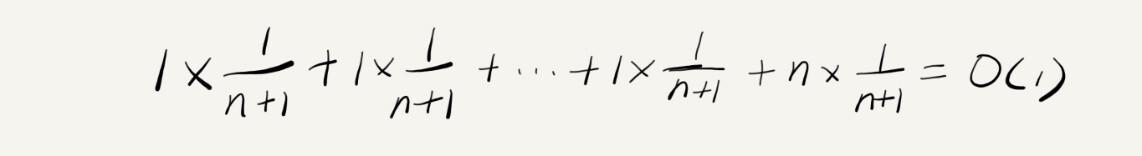110.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

class Solution {
    public boolean isBalanced(TreeNode root) {
        int dfs = dfs(root);
        return dfs != -1;
    }

    private int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int left = dfs(node.left);
        int right = dfs(node.right);
        if (left == -1 || right == -1) {
            return -1;
        }
        if (Math.abs(left - right) <= 1) {
            return Math.max(left, right) + 1;
        }
        return -1;
    }
}

二叉树从下往上遍历，后序遍历，对于每个节点，如果左右节点中有一个返回-1，即不是平衡二叉树，那么算上当前这个根节点也还是不平衡，所以直接返回-1，如果左右子树是平衡的，那么比较二者深度差是否小于1，小于则返回左右子树中的深度较大者+1，否则返回-1。
时间复杂度O（n），空间复杂度O（n）

257.二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。

public List<String> binaryTreePaths(TreeNode root) {
        dfs(root);
        return res;
    }

    private List<String> res = new ArrayList<>();
    private List<String> path = new ArrayList<>();

    private void dfs(TreeNode node) {
        path.add(String.valueOf(node.val));
        if (node.left == null && node.right == null) {
            StringBuilder sb = new StringBuilder();
            for (String s : path) {
                sb.append(s);
                sb.append("->");
            }
            res.add(sb.substring(0, sb.length() - 2));
            return;
        }
        if (node.left != null) {
            dfs(node.left);
            path.remove(path.size() - 1);
        }
        if (node.right != null) {
            dfs(node.right);
            path.remove(path.size() - 1);
        }
    }

404.左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        dfs(root, false);
        return res;
    }

    private int res = 0;
    private void dfs(TreeNode node, boolean isLeft) {
        if (node == null) {
            return;
        }
        if (isLeft && node.left == null && node.right == null) {
            res += node.val;
        }
        dfs(node.left, true);
        dfs(node.right, false);
    }
}

class Solution {
    /**
     * root 9999
     * left 8888
     * right 7777
     * @param root
     * @return
     */
    public int sumOfLeftLeaves(TreeNode root) {
        int res = 0;
        if (root == null) {
            return res;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);
        queue.add(new TreeNode(9999));
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            TreeNode tmp = queue.poll();
            if (tmp.val == 8888 && node.left == null && node.right == null) {
                res += node.val;
            }
            if (node.left != null) {
                queue.add(node.left);
                queue.add(new TreeNode(8888));
            }
            if (node.right != null) {
                queue.add(node.right);
                queue.add(new TreeNode(7777));
            }
        }
        return res;
    }
}

513.找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。

class Solution {
    private int ans;
    private int maxDepth = 0;
    public int findBottomLeftValue(TreeNode root) {
        ans = root.val;
        dfs(root, 1);
        return ans;
    }

    private void dfs(TreeNode node, int depth) {
        if (node == null) {
            return;
        }
        if (node.left == null && node.right == null && depth > maxDepth) {
            maxDepth = depth;
            ans = node.val;
        }
        dfs(node.left, depth + 1);
        dfs(node.right, depth + 1);
    }
}

有个理解错了的地方是，找最底层最左边的数，并不是一定得是左子树，没有左子树右子树第一个出现也是可以的，答案就是这个右叶子节点。

112.路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        dfs(root);
        for (Integer num : res) {
            if (num == targetSum) {
                return true;
            }
        }
        return false;
    }

    private List<Integer> res = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    private void dfs(TreeNode node) {
        path.add(node.val);
        if (node.left == null && node.right == null) {
            int sum = 0;
            for (Integer i : path) {
                sum += i;
            }
            res.add(sum);
        }
        int left = 0;
        int right = 0;
        if (node.left != null) {
            dfs(node.left);
            path.remove(path.size() - 1);
        }

        if (node.right != null) {
            dfs(node.right);
            path.remove(path.size() - 1);
        }
    }
}

113.路径总和II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

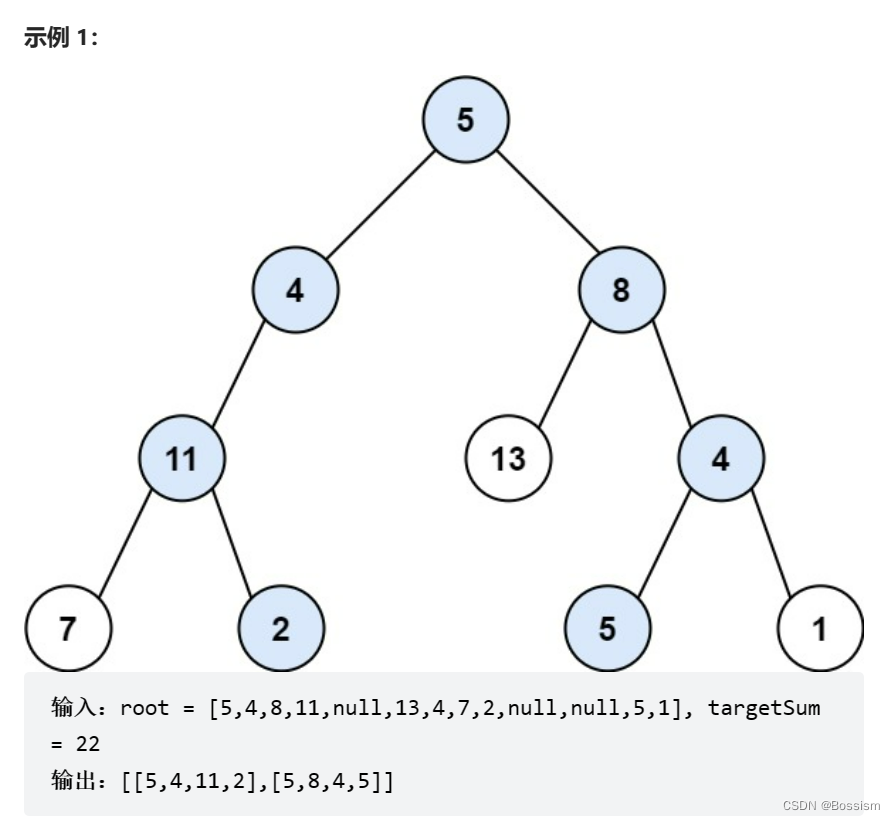
class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if(root == null){
            return new ArrayList<>();
        }
        dfs(root, 0, targetSum);
        return res;
    }

    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    
    private void dfs(TreeNode node, int sum, int target) {
        path.add(node.val);
        sum += node.val;
        if (node.left == null && node.right == null) {
            if (sum == target) {
                res.add(new ArrayList<>(path));
            }
            return;
        }
        if (node.left != null) {
            dfs(node.left, sum, target);
            path.remove(path.size() - 1);
        }
        if (node.right != null) {
            dfs(node.right, sum, target);
            path.remove(path.size() - 1);
        }
    }
}