常见排序算法--Java实现
- 插入排序
- 直接插入排序
- 折半插入排序
- 希尔排序
- 交换排序
- 冒泡排序
- 快速排序
- 选择排序
- 直接选择排序
- 堆排序
- 归并排序
- 基数排序
- 各种排序方法比较
在网上找了些排序算法的资料。此篇笔记本人总结比较,简单注释,觉得比较好理解,且相对简短方便记忆。
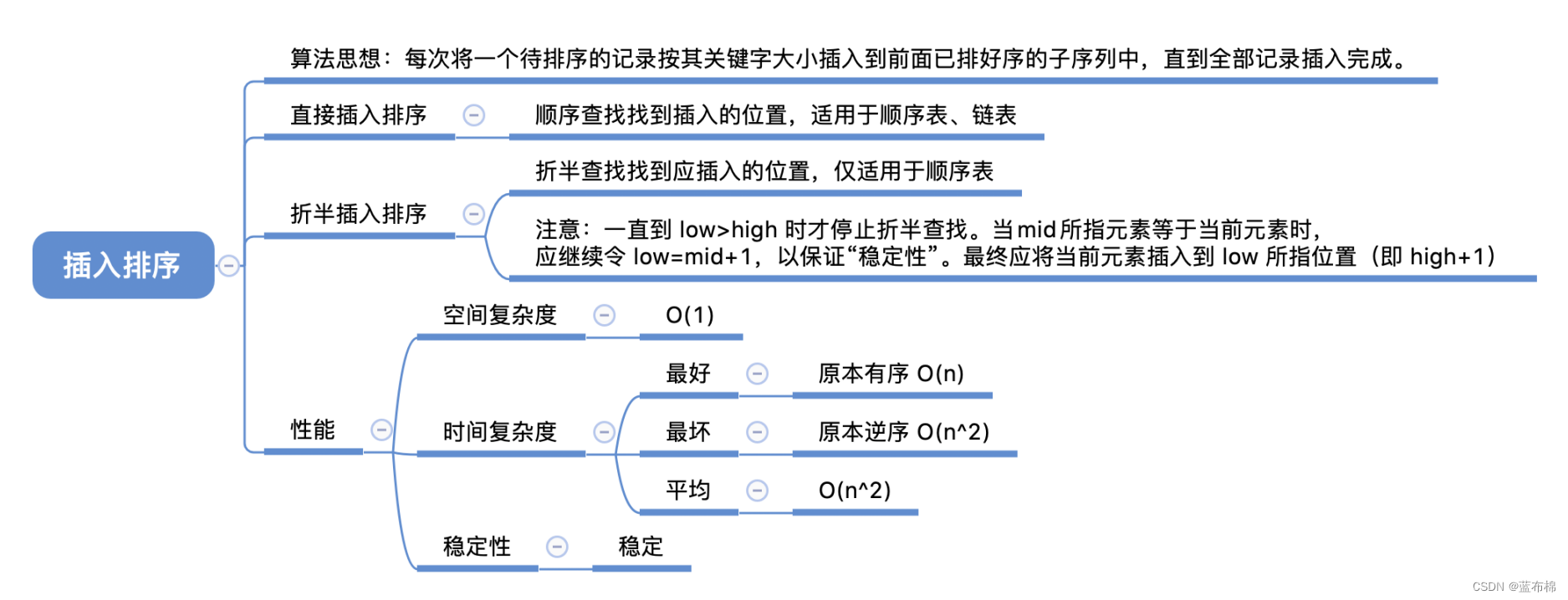
插入排序
直接插入排序
- 默认第0个有序,后面挨个插入前面有序的数中(像打扑克插牌一样)
/**
*(直接)插入排序
* 默认第0个有序,后面挨个插入前面有序的数中(像打扑克插牌一样)
*/
public static void ChaRu(int a[], int n){
int i,j;
// 第0个有序,从第1个开始
for(i = 1; i < n; i++){
int temp = a[i]; // 要插入的元素保存起来
// 在前面i-1个有序数组中,找插入的下标
for(j = i - 1; j >= 0 && temp < a[j]; j--){
a[j + 1] = a[j]; // 移动,覆盖
}
a[j + 1] = temp; // 找到位置了,插入,继续把后面的插入,循环
}
}
折半插入排序
- 折半插入排序(增加二分查找)
/**
* 折半插入排序(增加二分查找)
*/
public static void ZheBanCha(int a[], int n){
int i, j;
for(i = 1; i < n; i++){
int temp = a[i]; // 待插入的元素
// 二分查找法,找插入的位置
int left = 0, right = i - 1; // 0开始
while(left <= right){
int mid = (left + right) / 2;
if(temp < a[mid]) right = mid - 1;
else left = mid + 1;
} // right + 1 为插入的位置
// 统一后移元素,空出插入位置
for(j = i - 1; j >= right + 1; j--){ // >=
a[j + 1] = a[j];
}
a[right + 1] = temp; // right + 1 插入
}
}
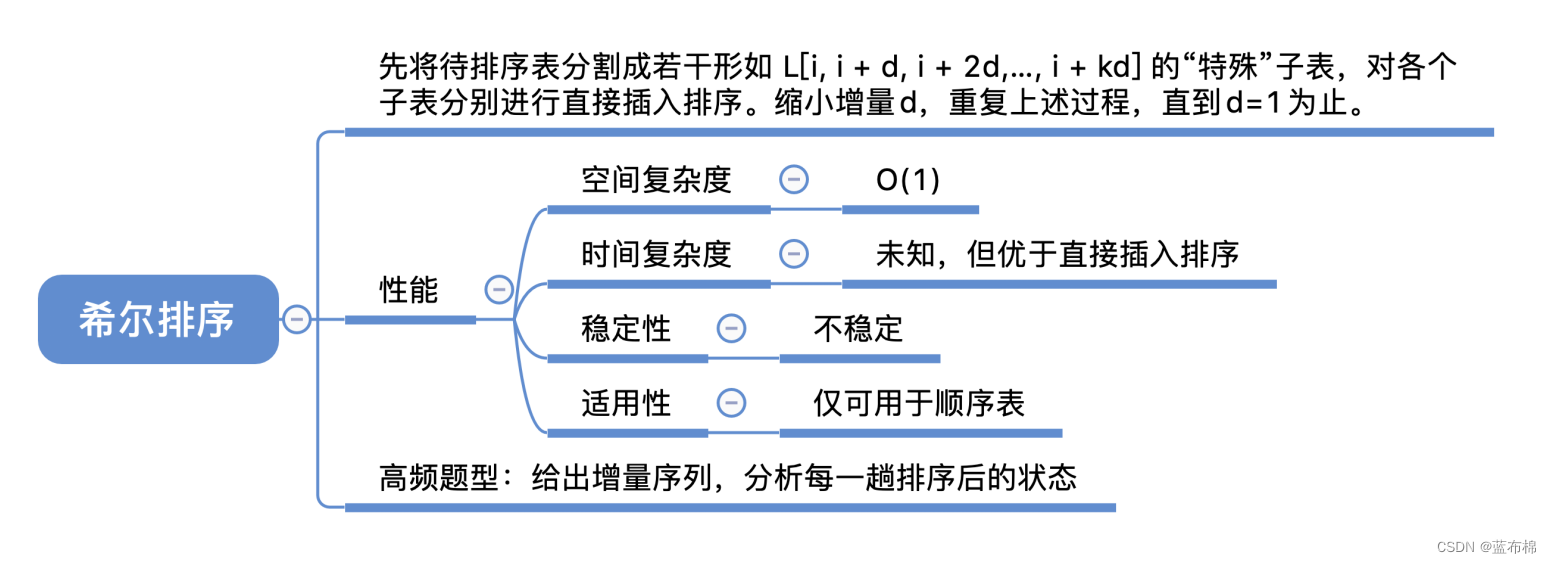
希尔排序
- 希尔排序(新增for循环,步长为有序增量表:4,2,1)[把1变成d]
/**
* 希尔排序(新增for循环,步长为有序增量表:4,2,1)[把1变成d]
*/
public static void shell(int[] a, int n) {
int d, i, j;
// 步长变化,每次减半,直到为1
for(d = n / 2; d >= 1; d = d / 2){ // 新增for步骤
for(i = d; i < n; i++){ // 1 -> d
int temp = a[i];
for(j = i - d; j >= 0 && temp < a[j]; j -= d){
a[j + d] = a[j];
}
a[j + d] = temp;
}
}
}
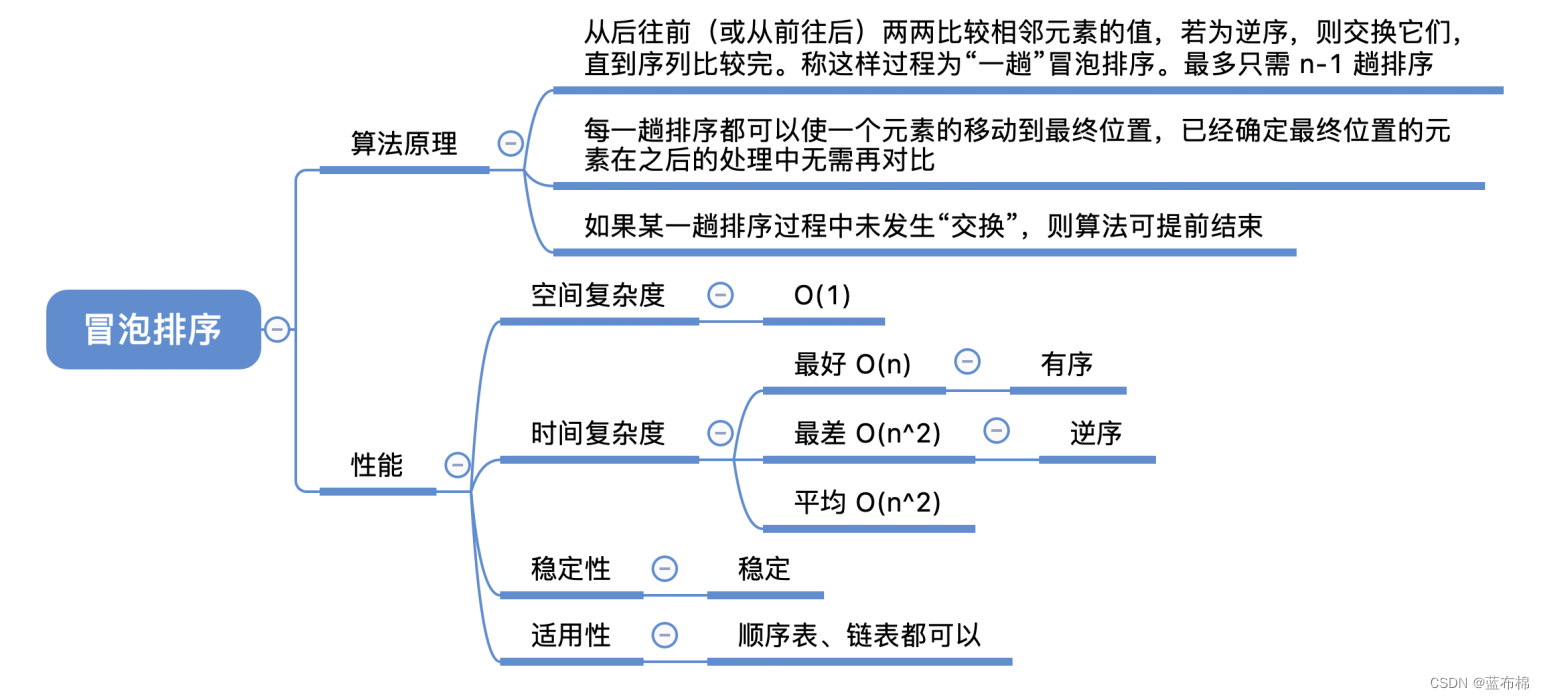
交换排序
冒泡排序
- 每一趟都会把最大的数排到最后,然后继续看前面的,不管最后的了(因为后面有序了)
/**
* 冒泡排序(加了flag优化)
* 每一趟都会把最大的数排到最后,然后继续看前面的,不管最后的了(因为后面有序了)
*/
public static void MaoPao(int[] a, int n) {
for(int i = 0; i < n; i++){ // i趟数
boolean flag = false; // 提前退出冒泡循环的标志位
for(int j = 0; j < n - i - 1; j++){
if(a[j] > a[j+1]){ // 比后面大,就交换
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
flag = true; // 表示有数据交换
}
}
if(flag == false) return; // 本趟没有数据交换,提前退出
}
}
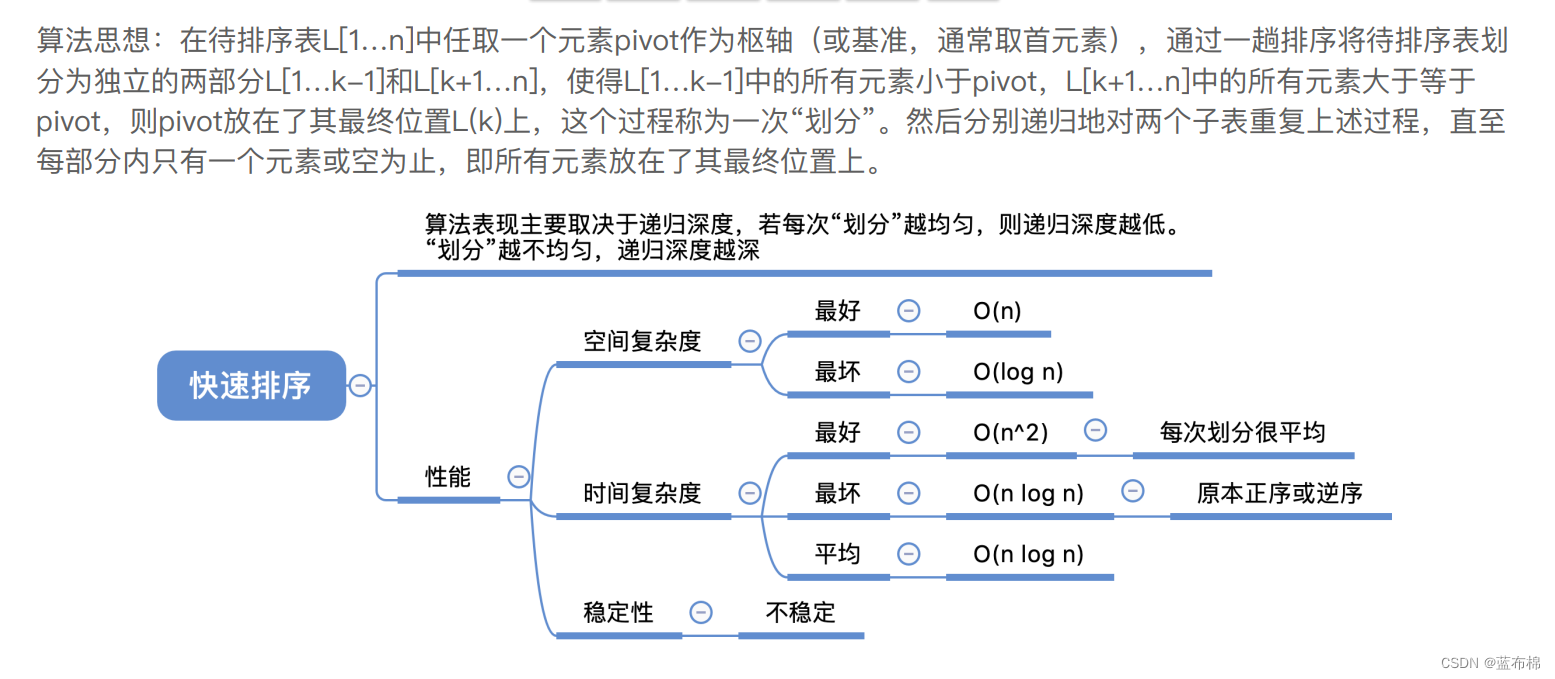
快速排序
- 快速排序(递归,轴,划分左右){ 轴元素放到最终位置,[比轴小,轴,比轴大] }
- 与其他排序算法相反的是:元素越有序,快排时间复杂度越高
/**
* 快速排序(递归,轴,划分左右){轴元素放到最终位置,[比轴小,轴,比轴大]}
* 与其他排序算法相反的是:元素越有序,快排时间复杂度越高
*/
public static void QuickSort(int[] a, int low, int high) {
if(low < high) { // 递归跳出的条件
int pivot = patition(a, low, high); // 划分函数
QuickSort(a, low, pivot - 1); // 划分左子表
QuickSort(a, pivot + 1, high); // 划分右子表
}
}
// 用第一个元素将待排序列划分为左右两个部分(比轴小,比轴大)
public static int patition(int[] a, int low, int high) {
int pivot = a[low]; // (暂存)第一个元素作为轴
while(low < high) { // 用low,high寻找轴的最终位置
while(low < high && a[high] >= pivot) high--;
a[low] = a[high]; // 比轴小的移到左端
while(low < high && a[low] < pivot) low++;
a[high] = a[low]; // 比轴大的移到右端
}
a[low] = pivot; // 轴元素放到最终位置*
return low; // 返回存放轴的最终位置
}
选择排序
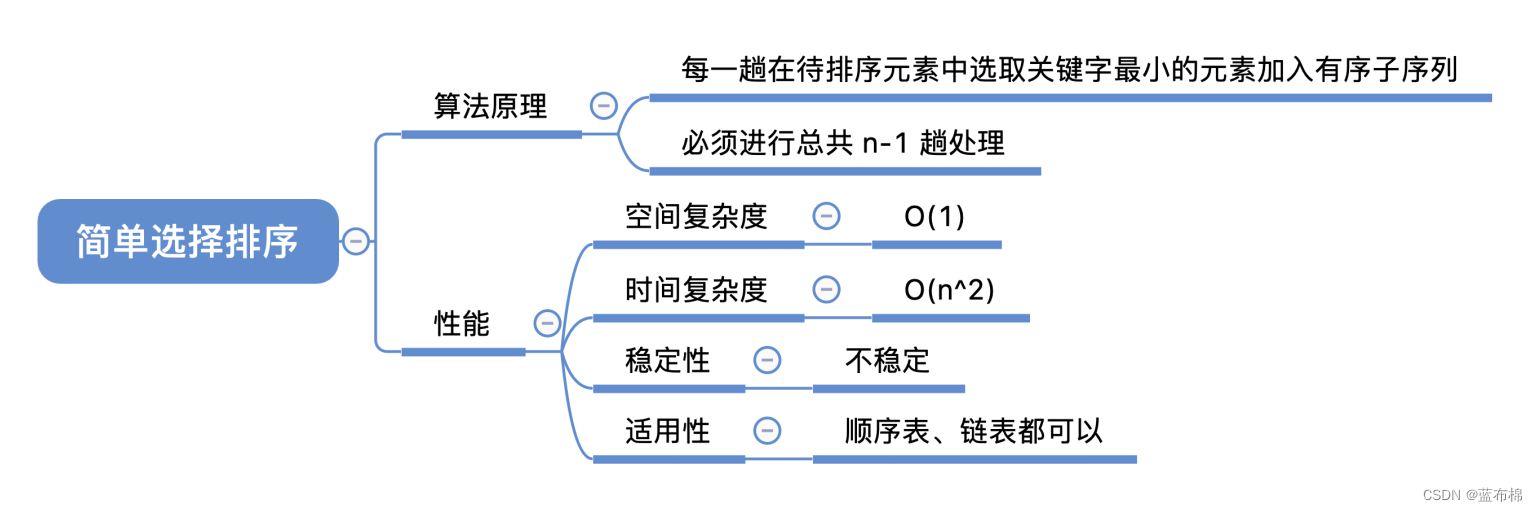
直接选择排序
- 简单选择排序(每趟选一个最小的元素,交换到前面)
/**
* 简单选择排序(每趟选一个最小的元素,交换到前面)
*/
public static void JianDanXuanZe(int[] a, int n) {
for(int i = 0; i < n -1; i++){ // 总共n-1趟,最后一次就不用了
int min = i; // 记录此趟最小元素位置
for(int j = i + 1; j < n; j++) { // 再a[i..n-1]中选择最小元素
if(a[j] < a[min]) min = j; // 更新最小元素位置
}
if(min != i) { // 交换,把最小值放到i的位置
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}
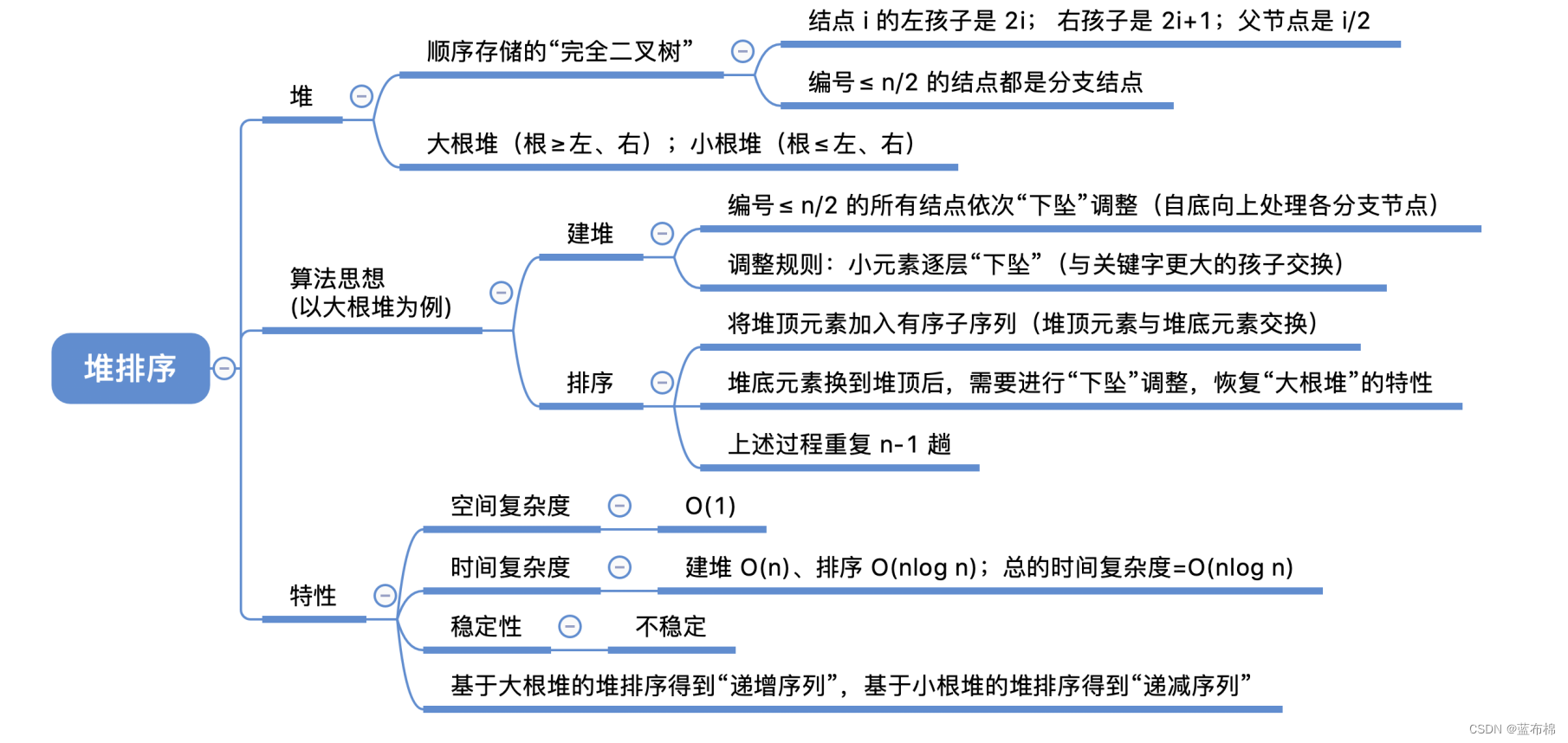
堆排序
/**
* 堆排序(从小到大)
*/
public static void heapSortAsc(int[] a, int n) {
int i,tmp;
// 从(n/2-1) --> 0逐次遍历。遍历之后,得到的数组实际上是一个(最大)二叉堆。
for (i = n / 2 - 1; i >= 0; i--)
maxHeapDown(a, i, n-1);
// 从最后一个元素开始对序列进行调整,不断的缩小调整的范围直到第一个元素
for (i = n - 1; i > 0; i--) {
// 交换a[0]和a[i]。交换后,a[i]是a[0...i]中最大的。
tmp = a[0];
a[0] = a[i];
a[i] = tmp;
// 调整a[0...i-1],使得a[0...i-1]仍然是一个最大堆。
// 即,保证a[i-1]是a[0...i-1]中的最大值。
maxHeapDown(a, 0, i-1);
}
}
/**
* (最大)堆的向下调整算法
*
* 注: 数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N为数组下标索引值,如数组中第1个数对应的N为0。
*
* 参数说明:
* a -- 待排序的数组
* start -- 被下调节点的起始位置(一般为0,表示从第1个开始)
* end -- 截至范围(一般为数组中最后一个元素的索引)
*/
public static void maxHeapDown(int[] a, int start, int end) {
int c = start; // 当前(current)节点的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 当前(current)节点的大小
for (; l <= end; c=l,l=2*l+1) {
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] < a[l+1])
l++; // 左右两孩子中选择较大者,即m_heap[l+1]
if (tmp >= a[l])
break; // 调整结束
else { // 交换值
a[c] = a[l];
a[l]= tmp;
}
}
}
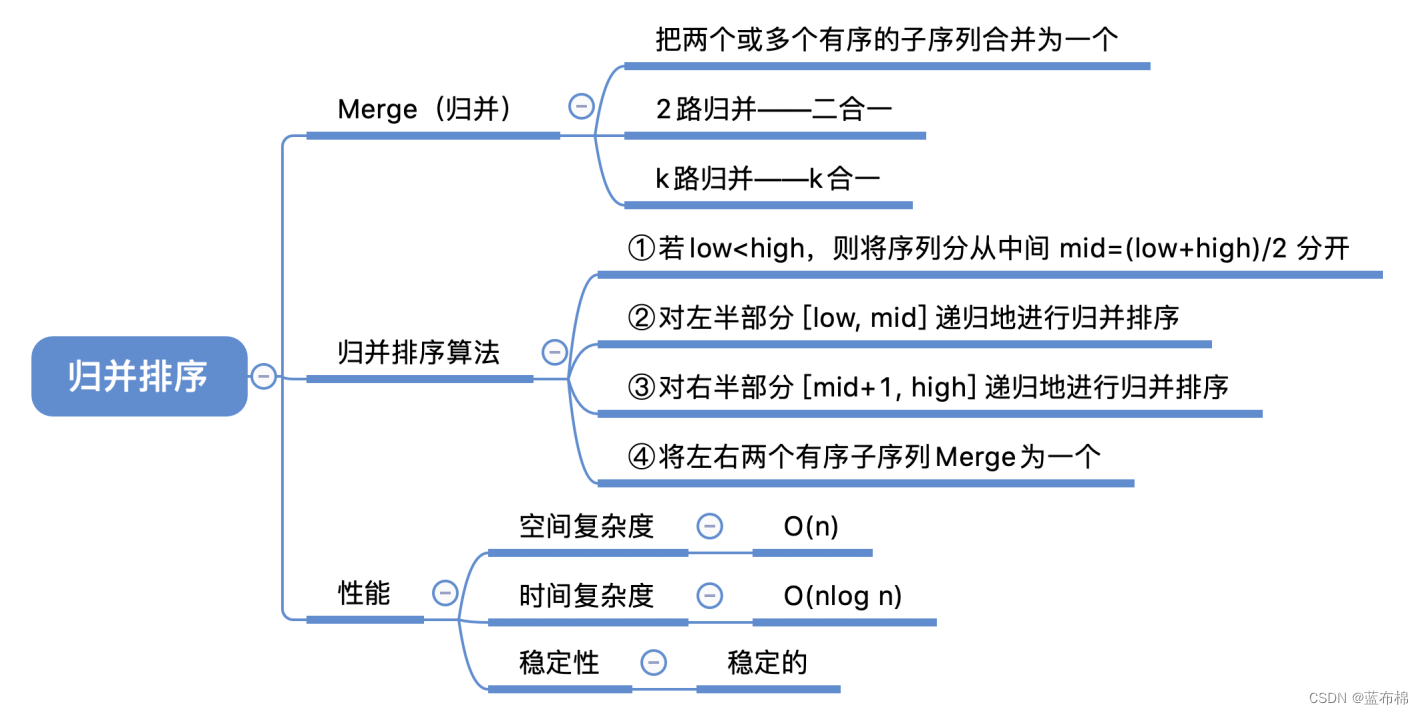
归并排序
- 归并排序(辅助数组,递归,分治,合并)
/**
* 归并排序(辅助数组,递归,分治,合并)
*/
int[] tmp = new int[a.length]; // 新建一个临时数组存放*
public static void mergeSort(int[] a, int low, int high, int[] tmp) {
if(low < high){
int mid = (low + high) / 2; // 从中间划分
mergeSort(a, low, mid, tmp); // 对左半部分归并排序
mergeSort(a, mid + 1, high, tmp); // 对右边部分归并排序
// (上面两步递归,一直划分到每个子序列只含有一个元素)
merge(a, low, mid, high, tmp); // 合并两个有序序列(归并)
}
}
// a[low..mid] 和 a[mid+1..high] 将两个部分归并(合并)
public static void merge(int[] a, int low, int mid, int high, int[] tmp) {
int i, j, k;
// 将a[] 中所有元素复制到 tmp[]辅助数组
for(k = low; k <= high; k++) {
tmp[k] = a[k];
}
// 两个区间,两个指针 i,j;比较,将较小值复制到 a[]中
for(i = low, j = mid + 1, k = i; i <= mid && j <= high; k++){
if(tmp[i] < tmp[j])
a[k] = tmp[i++];
else
a[k] = tmp[j++];
}
// 若左右序列还有剩余,则将其全部拷贝进 a[]中
while(i <= mid) a[k++] = tmp[i++];
while(j <= high) a[k++] = tmp[j++];
}
基数排序
- 基数排序(分配,收集)
**
* 基数排序(分配,收集)
* 个位分配,收集;十位分配,收集;...
*/
public static void radixSort(int[] a){
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10
// 获取数组a中最大值
int max = a[0];
for(int i = 1; i < a.length; i++){
if(a[i] > max) max = a[i];
}
// 从个位开始,对数组a按"指数"进行排序(个位,十位,百位。。。)
for(exp = 1; max / exp > 0; exp *= 10){
int[] output = new int[a.length]; // 存储"被排序数据"的临时数组
int[] buckets = new int[10]; // 桶 0-9
// 将数据出现的次数存储在buckets[]中
for(int i = 0; i < a.length; i++){
buckets[(a[i] / exp) % 10]++;
}
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for(int i = 1; i < 10; i++){
buckets[i] += buckets[i - 1];
}
// 将数据存储到临时数组output[]中
for(int i = a.length - 1; i >= 0; i--){
output[buckets[(a[i] / exp) % 10] - 1] = a[i];
buckets[(a[i] / exp) % 10]--;
}
// 将排序好的数据赋值给a[]
for (int i = 0; i < a.length; i++) {
a[i] = output[i];
}
}
}

各种排序方法比较
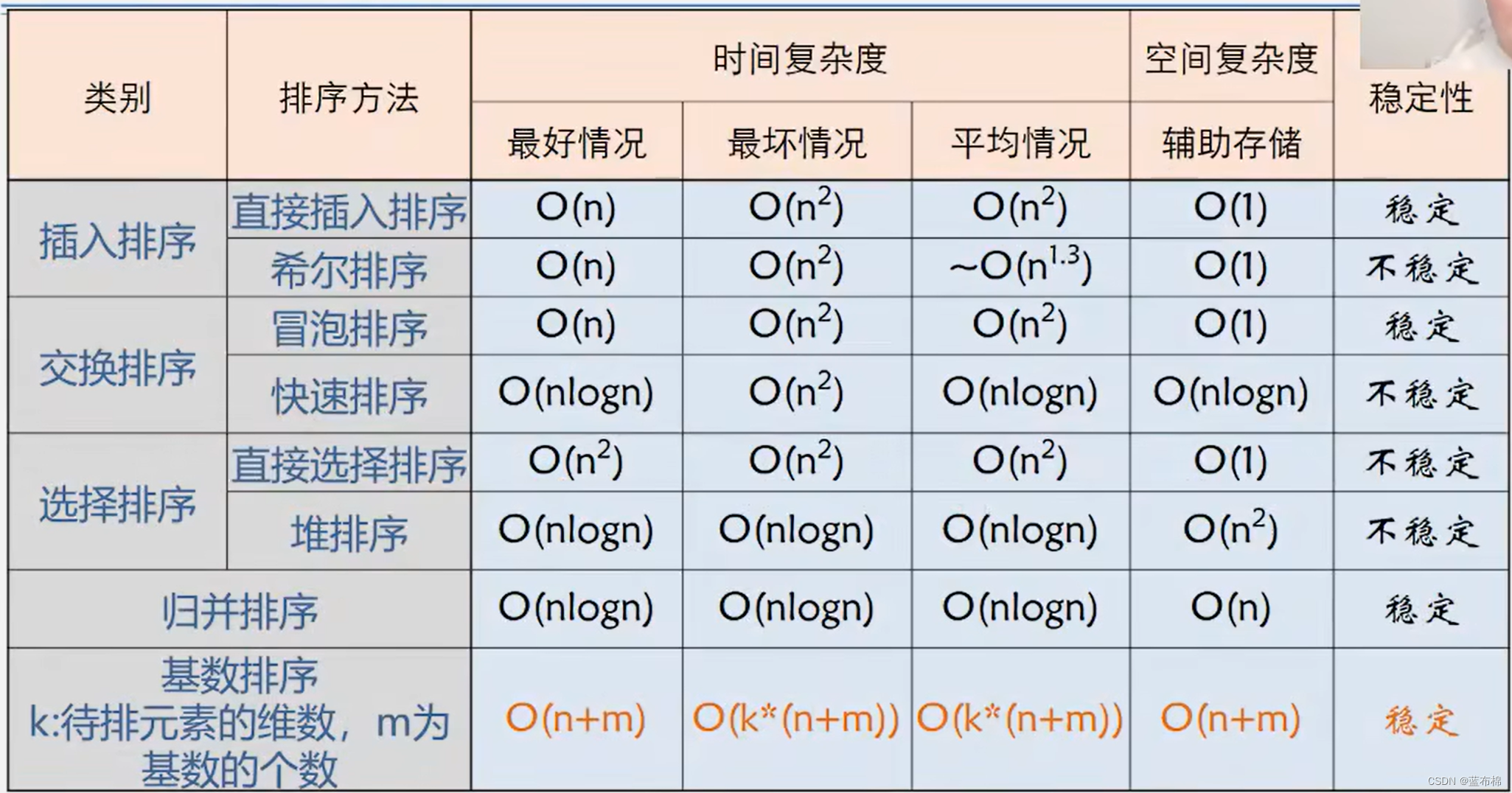
引用:
代码后面附的总结PPT为王道数据结构课件截图
排序方法比较图片为青岛大学王卓老师的数据结构课件截图